
- Reasoning - Home
- Reasoning - Overview
- Reasoning
Reasoning - Coded Binary Numbers
The number which has base 2 is known as binary number. Binary number is made by 0s and 1s complements. So, coded binary number consists of two processes. One is conversion of binary to decimal and another is decimal to binary.
Decimal Numbers
To know what binary number is, first we have to know about decimal numbers. So, decimal number consists of ten digits (i.e. 0,1,2,3,4,5,6,7,8,9). Any decimal system can be represented by using these numbers. For example, a sequence of digits is 2, 4, 6 and 8. We do it in the following manner −
2468 = 2 103 + 4 102 + 6 101 + 8 100
= 2468
Note − We get the value of numbers in this case by multiplying different digits of sequence by powers of 10 and adding. Here this 10 is called base or radix. Therefore under a decimal system our base is 10.
Binary Numbers
We use ten digits to represent a decimal number; like that we use only two digits to represent binary number. Any number can be represented by using these two digits i.e. 0 and 1.
Example of a binary number is- 1101. Here 4 digits are present in the sequence of digits − 1, 1, 0, 1. We get the value in the following manner.
1101 = 1 23 + 1 22 + 0 21 + 1 20
= 8 + 4 + 0 + 1 = 13
Thus, the binary number represents thirteen in decimal system. The value can be determined by multiplying different digits of sequence by powers of 2 and adding.
Conventional method − In the above example, we see that to get the value of any binary number, we use the following rule −
The first digit from right is multiplied by 20 = 1
The second digit from right is multiplied by 21 = 2
The third digit from right is multiplied by 22 = 4
Similarly, nth digit from right is multiplied by 2n1
Finally, all these are added.
For Example − Convert the following binary numbers into decimal numbers.
A - 1010
B - 1111
C - 100
D - 10000
Solution −
A - 1010 = 1 23 + 0 22 + 1 21 + 0 20
B - 1111 = 1 23 + 1 22 + 1 21 + 1 20
C - 100 = 1 22 + 0 21 + 0 20
D - 10000 = 1 24 + 0 23 + 0 22 + 0 21 + 0 20
Quicker Method
Step I − Starting from right digit of given number, write 1, 2, 4, 8, 16, 32. and so on below each digit as you proceed towards left.
Step II − Ignore the numbers below 0s. Add all numbers below 1s.
Lets solve the example 1 by this method.
A - 1010
We will use 1,2,4,8 because here 4 digits are present.
We get,
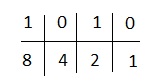
4 and 1 fall below the zeroes. We ignore them and add the remaining. We get 8 + 2 = 10
Like this we can solve other numbers.
Decimal number can be converted to binary by the method of successive divisions. Each time of division, the dividend is divided by 2. The reminder is noted and quotient becomes the next dividend, which is again divided by 2. The process is repeated until no more division is possible.
For Example − convert 17 into binary number −
Divide 17 by 2 until no more division is possible.
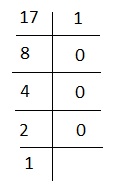
So, the binary form of 17 is 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
In a certain code, the symbol for 0 is + and for 1 is #. No number or symbol is greater than 1. The value of symbol for 1 doubles itself every time it shifts one place to the left.
0 is depicted as +
1 is depicted as #
2 is depicted as #+
3 is depicted as ##
4 is depicted as #++ and so on
1 - Which of the following will represent 11?
Options −
A - #+##
B - +##+
C - ##++
D - #+#++
E - none of these
Answer − Option A
Explanation − To get equivalent of 11, we use the method of successive division by 2.
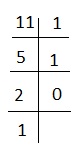
So the binary form will be 10111. Replacing 1 and 0 by # and + we will get #+##.
2 - Which of the following will represent 8?
Options −
A - ##++
B - +##+
C - ##++
D - ++##
E - none of these
Answer − Option E
Explanation − for 8, we have-
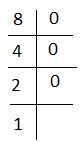
i.e. 1000 or #+++. Correct choice is 5.
3 - Which of the following will be represented by ##+#?
Options −
A - 8
B - 11
C - 13
D - 12
E - none of these
Answer − Option E
Explanation − ##+# = 1101 = 1 23 + 1 22 + 0 21 + 1 20 = 15
4 - Which of the following number will be represented by #+++#?
Options −
A - 22
B - 31
C - 14
D - 17
E - none of these
Answer − Option D
Explanation − # + + + # = 10001
= 1 24 + 0 23 + 0 22 + 0 21 + 1 20
= 16 + 1 = 17
Binary systems have base 2, a decimal system has base 10, and tertiary system has base 3, whereas octal system has base 8. In case of tertiary, we have three digits to represent numbers. These are 0, 1 and 2. In this case numbers will be converted to decimal by multiplying with appropriate powers of 3.
For Example −
(12012)3 = 1 34 + 2 33 + 0 32 + 1 31 + 2 30 = (104)3