
- Reasoning - Home
- Reasoning - Overview
- Reasoning
Coded Binary Numbers Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Coded Binary Numbers. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

Go through the following information and answer the question carefully.
In a certain code, the symbol for 0 (zero) is * and for 1 is Δ. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be depicted using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
0 is depicted as *
1 is depicted as Δ
2 is depicted as Δ*
3 is depicted as Δ Δ
4 is depicted as Δ** and so on.
Q 1 - Which of the following will represent 9?
Options :
Answer : C
Explanation
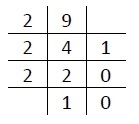
Thus (9)10 = (1001), = Δ**Δ
Go through the following information and answer the question carefully.
In a certain code, the symbol for 0 is * and for 1 is Δ. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be depicted using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is depicted as *
'1'is depicted as Δ
'2' is depicted as Δ*
'3' is depicted as ΔΔ
'4' is depicted as Δ** and so on
Q 2 - Which of the following codes will give odd number as the result after being decoded?
Options :
Answer : A
Explanation
Since I is depicted as Δ, the code which will end with Δ will give odd number as a result, Obviously, it is option A.
Go through the following information and answer the question carefully.
Symbols for 0 is < and for 1 is }. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be depicted using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is written as <
'1' is written as }
'2' is written as }<
'3' is written as }}
'4' is written as }<< and so on.
Q 3 - Which of the following will represent the value of }}<}?
Options :
Answer : D
Explanation
| } | } | < | } |
| 8 | 4 | 2 | 1 |
Since < is he code for 0, ignore the value written below <. Thus }}<} = 8 + 4 + 0 + 1 = 13
Go through the following information and answer carefully.
Symbol for 0 is % and for 1 is ). There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be depicted using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is written as %
'1' is written as )
'2' is written as )%
'3' is written as ))
'4' is written as )%% and so on.
Q 4 - The HCF of ))%%) and )))) is
Options :
Answer : C
Explanation
))%%) = 11001
1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20
= 16 + 8 + 1 = 25
)))) ⇒ 1111 ⇒ 23 + 22 + 21 + 20
= 8 + 4 + 2 + 1 = 15
HCF of 25 and 15 = 5
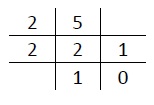
Thus (5)10 = (101)2 = )%)
Go through following information and answer the question accordingly.
In a certain code, the symbol for 0 is ! and for 1 is +. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be depicted using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is depicted as !
'1' is depicted as +
'2' is depicted as +!
'3' is depicted as ++
'4' is depicted as +!! and so on
Q 5 - Which of the following will represent 8?
Options :
Answer : E
Explanation
(8)10 = (1000)2 = +!
Go through the following question and answer accordingly.
In a certain code, the symbol for 0 (zero) is Δ and for 1 is *. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be written using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is depicted as Δ
'1' is depicted as *
'2' is depicted as *Δ
'3' is depicted as **
'4' is depicted as *Δ Δand so on.
Q 6 - The symbol combination *Δ Δ** represents which of the following numbers?
Options :
Answer : E
Explanation
Put 1,2,4, 8 and so on below each symbol starting from the right end of the symbol combination, We get
| * | Δ | Δ | * | * |
| 16 | 8 | 4 | 2 | 1 |
Now, Since Δ stands for 0, therefore, reject all the values depicted below Δ s. Thus reject 8 and 4. Now, add the remaining values under each *. Hence the required value of *Δ Δ** is 16 + 2 + 1 = 19.
Go through the following information and answer the question accordingly.
In a certain code, the symbol for 0 is * and for 1 is Δ . There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be written using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
0 is written as *
1 is written as Δ
2 is written as Δ*
3 is written as Δ Δ
4 is written as Δ** and so on.
Q 7 - Which of the following will represent 37?
Options :
Answer : A
Explanation
The decimal to binary conversions will be (37)10 = (100101)2
Try to solve the questions by deep analyzing the given information.
In a certain code, the symbol for 0 (zero) is Δ and for 1 is +. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be written using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
'0' is written as Δ
'1' is written as +
'2' is written as +Δ
'3' is written as ++
'4' is written as +Δ Δand so on.
Q 8 - The symbol arrangement ++Δ Δ+Δ represents which of the following numbers?
Options :
Answer : D
Explanation
| + | + | Δ | Δ | + | Δ |
| 32 | 16 | 8 | 4 | 2 | 1 |
Now since Δ is the code for 0. Therefore, ignore all the values written below Δ. Thus ++Δ Δ+Δ = 32 + 16 + 2 = 50
Try to solve the questions by deep analyzing the given information.
In a certain code, the symbol for 0 is + and for 1 is *. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be written using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
0 is written as +
'1' is written as *
2 is written as *+
3 is written as **
4 is written as *++ and so on
Q 9 - Which of the following will represent 2 x 2 + 3 x 3 + 2 x 3?
Options :
Answer : B
Explanation
The given equation can be calculated as 2 x 2 + 3 x 3 + 2 x 3 = 19. After dividing 19 with 2, we can get remainders as 10011 which means the answer is *++**.
Try to solve the questions by deep analyzing the given information.
In a certain code, the symbol for 0 is ! and for 1 is #. There is no symbol for rest of the numbers. Numbers greater than 1 are needed to be written using the two given symbols. Left shifting of 1 doubles its value each time. Study the following example.
0 is written as !
1 is written as #
2 is written as #!
3 is written as ##
4 is written as #!! and so on
Q 10 - Which of the following no will be represented by ###.
Options :
Answer : B
Explanation
### can be represented as 111 it means 4 + 2 + 1 = 7.