
- Reasoning - Home
- Reasoning - Overview
- Reasoning
Reasoning - Clock
The hands of a clock can have a maximum angle of 180o between them. When this happens, both the hands represent a straight line.
The hands of a clock make right angles twice every hour when they are 15 minutes away from each other.
The two hands of a clock coincide once in every hour.
A clock is very essential for every human being to schedule their daily tasks. The clock theory is related to everyday life.
A clock is an instrument that displays time by dividing it into hours, minutes, and seconds.
Dial
It has a circular dial numbered from 1 to 12 that indicates the hours. The circumference of a dial is further divided into 60 equal spaces, that are called the minutes spaces.
1 hour = 60 minutes
1 minute = 60 seconds and
1 hour = 3600 seconds
Tricks
Between n and (n+1) O`clock, the two hands of a clock will coincide at $\left ( \frac{60n}{11} \right )$ min past n.
Between n and (n+1) O`clock, the two hands of a clock will mutually make a right angle at $\left ( 5n \pm 15 \right )\times\frac{12}{11}$ min past n.
-
Between n and (n+1) O`clock, the hands of a clock will be in a straight line (without being together) at
$\left ( 5n - 30 \right )\times\frac{12}{11}$ min past n,(when n >6)
$\left ( 5n + 30 \right )\times\frac{12}{11}$ min past n,(when n <6)
Between n and (n+1) O`clock, the hands of a clock are $x$ min apart at $\left ( 5n \pm x \right )\times\frac{12}{11}$ min past n. + sign indicates that the minute hand is ahead and sign indicates that the hour hand is ahead.
If the minute hand of a clock overtakes the hour hand at an interval of $x$ min of the correct time, then the clock loses or gains by $\left ( \frac{720}{11} - x \right )\left ( \frac{60 \times 24}{x} \right )$ min.
1 − At what time between 7.15 and 8.15, the hands of a clock will coincide each other?
Options −
A - $39\frac{5}{11}$
B - $39\frac{4}{11}$
C - $38\frac{5}{11}$
D - $39\frac{4}{11}$
Answer − A
Explanation −
$\frac{60 \times n}{11} = \frac{60}{11} \times \frac{29}{4} = 39\frac{5}{11}$
Where $n = 7.15 = 7\frac{15}{60} = \frac{29}{4}$
2 − In what particular time, between 9 and 8 Oclock, both the hands will be at a right angle to each other?
Options −
A - $65\frac{4}{11}$ and $32\frac{7}{11}$ min past 9
B - $65\frac{2}{11}$ and $32\frac{2}{11}$ min past 9
C - $65\frac{3}{11}$ and $32\frac{3}{11}$ min past 9
D - $65\frac{1}{11}$ and $32\frac{1}{11}$ min past 9
Answer − A
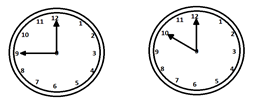
Explanation −
$\left ( 5n \pm 15 \right ) \times\frac{12}{11} = \left ( 5\times9\pm 15 \right )\times\frac{12}{11}$
$= 65\frac{4}{11}$ and $32\frac{7}{11}$ min past 9
3 − In between 12 and 1 O`clock, when will both the hands of a clock form a straight line?
Options −
A - $\frac{360}{11}$ min. past 12
B - $\frac{355}{11}$ min. past 12
C - $\frac{340}{11}$ min. past 12
D - $\frac{345}{11}$ min. past 12
Answer − D
Explanation −
$\left ( 5n-30 \right )\times\frac{12}{11}$ min past n
$\left ( 6-30 \right )\times\frac{12}{11}$ min. past 12
$= \frac{345}{11}$ min. past 12 (since n = 12)
4 − In how much time, hands of a clock will be in the 30 min. space apart when they are in between 12 and 1 p.m. on Monday?
Options −
A - $\frac{1080}{11}$ and $\frac{300}{11}$ min past 12
B - $\frac{1080}{12}$ and $\frac{360}{11}$ min past 12
C - $\frac{1080}{11}$ and $\frac{360}{11}$ min past 12
D - $\frac{1080}{12}$ and $\frac{300}{12}$ min past 12
Answer − C
Explanation −
$\left ( 5n\pm x \right )\times\frac{12}{11}$
$= \left ( 5\times12\pm 30 \right )\times\frac{12}{11}$
$= \frac{90\times12}{11}$ and $\frac{30\times12}{11}$ min past 12 = $\frac{1080}{11}$ and $\frac{360}{11}$ min past 12
5 − The minute hand of a clock overtakes the hour hand at interval of 61 min. then the clock loses or gain by how much time?
Options −
A - $104\frac{4}{671}$ min.
B - $105\frac{1}{671}$ min.
C - $104\frac{3}{671}$ min.
D - $105\frac{4}{671}$ min.
Answer − B
Explanation −
$\left ( \frac{720}{11}-61 \right )\times\left ( \frac{60\times24}{61} \right )$
$= 105\frac{1}{671}$ min.