Aptitude - Questions & Answers

Aptitude - Height & Distance Online Quiz

Quiz

Following quiz provides Multiple Choice Questions (MCQs) related to Height & Distance. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

Q 1 - A man observes the elevation of a balloon to be 45° at a point A .He then walks towards the balloon and at a certain place B finds the elevation to be 60°. He further walks in the direction of the balloon and finds it to be directly over him at a height of 450 m. Distance travelled from A to B is

Answer : A

Explanation

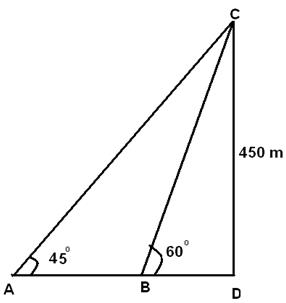
Height & Distance Solution 2

450/BD= tan (60) =>BD =450/√3
450/AD= tan (30) =>AD= 450√3
AD =BD +AB
=>AB=AD-BD= 450√3-450/√3=(450x3-450)/√3=300√3m

Q 2 - When the sun's altitude changes from 45° to 60°, the length of the shadow of a tower decreases by 45m. What is the height of the tower?

Answer : A

Explanation

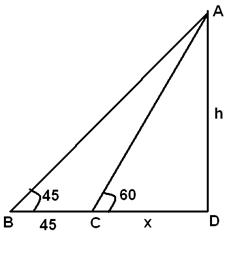
Height & Distance Solution 6

Let AD be the tower, BD be the initial shadow and CD be the final shadow.
Given that BC = 45 m,  ABD = 45°,  ACD = 60°,
Let CD = x, AD = h
From the right   CDA, tan60=h/x
From the right   BDA, tan45=(45+x)/h=>h=45+x
=>h=45+h/√3
=>h(1-1/√3)=45
=>h=45/(1-1/√3)=(45√3)/(√3-1)

Q 3 - From the top of mast head of height 210 meters of a ship, a boat is observed at an angle of depression of 30° then the distance between them is

Answer : A

Explanation

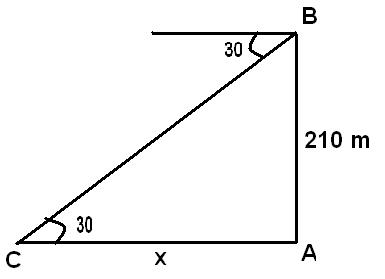
Height & Distance Solution 7

From the right angled triangle CAB
Tan(30) =210/X
=>X=210/Tan(30)=210/(1/√3)=210√3

Q 4 - The shadow of a building is 10 m long when the point of rise of the sun is 60°. Discover the building's stature.

Answer : B

Explanation

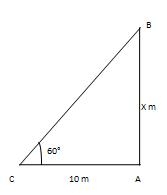
Height & Distance Solution 12

Let AB be the building and AC be its shadow.
Then, AC=20m and ∠ACB=60°.Let AB= x m.
Presently AB/AC=tan 60°=√3=>x/10=√3
=>x=10√3m= (10*1.732) m=17.32m.
∴ Height of the building is 17.32m.

Q 5 - Consider vertical shaft 6 m high has a shadow of length 2√3m, discover the angle of elevation of the sun?

Answer : A

Explanation

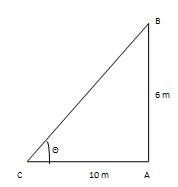
Height & Distance Solution 13

Let AB be the building and AC be its shadow. Then, AB= 6m and AC= 2√3m.
Let ∠ACB= θ Then tan θ = AB/AC= 6/2√3m
 =√3= >θ =60°
Point of rise of the sun is 60°

Q 6 - At a moment, the shadow's length of a shaft is √3 times the stature of the shaft. The edge of rise of the sun is:

Answer : A

Explanation

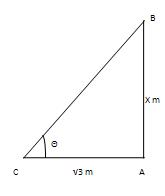
Height & Distance Solution 17

Let AB be the post and AC be its shadow.
Let AB =X m. Then, AC= √3Xm.Let∠ACB=θ.
AB/AC=tanθ => tanθ = X/√3X = 1/√3 =tan30°.
∴ θ = 30°.
Hence, the point of rise is 30°.

Q 7 - From The highest point of a bluff 90 m high, the edges of Misery of the top and base of a tower are seen to be 30° and 60°. What is the tower's tallness is?

Answer : C

Explanation

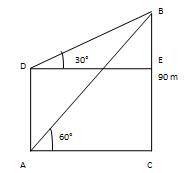
Height & Distance Solution 21

Let AB be the precipice and CD be the tower. Draw DE || CA.
Then, ∠BDE=30°, ∠BCA=60°and AB= 90m.
From right △CAB, we have
CA/AB=cost60°=1/√3 => CA/90=1/√3
=>CA=(90*1/√3* √3/√3)
=30 √3m.
∴ DE =CE=30/√3m.
From right ?DEB, we have
BE/DE= tan30°=1/√3 => BE/30 √3=1 √3
=>BE= (30 √3*1 √3) =30m.
∴ CD=AE= (AB-BE) = (90-30) m=60m.
Hence, the tower's stature is 60m.

Q 8 - From a point on a scaffold over the waterway, the edge of dejection of the banks on inverse sides of the waterway is 30°and 45°respectively. In the event that the scaffold is at tallness of 2.5m from the banks, find the width of the Stream. (Take √3=1.732)

Answer : B

Explanation

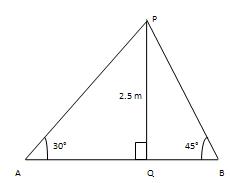
Height & Distance Solution 24

Let and B be two point on the banks on inverse sides of the stream.
Let P be a point on the scaffold at stature of 2.5m.
Let PQ-AB.
PQ=2.5m.∠BAP=30°and ∠ABP=45°.
QB/PQ=cot45°=1 => QB/2.5=1 => QB=2.5m.
AQ/PQ =cot30°=√3 => AQ/2.5= √3 => AQ= (2.5)√3m.
Width of the stream =AB= (AQ+QB)=2.5(√3+1)
5/2(1.732+1) m=6.83m.

aptitude_height_distance.htm

Print Page