
- Aptitude - Home
- Aptitude - Overview
- Quantitative Aptitude
Height & Distance - Solved Examples
Q 1 - From a point 375 meters away from the foot of a tower, the top of the tower is observed at an angle of elevation of 45°, then the height (in meters) of the tower is?
Answer - A
Explanation
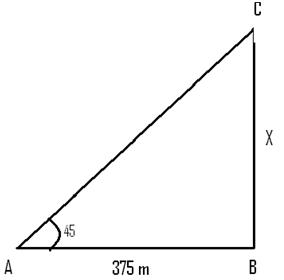
From the right angled triangle Tan(45°)= X/375 => X = 375 m
Q 2 - The angle of elevation of a tower at a point 90 m from it is cot-1(4/5).Then the height of the tower is
Answer - C
Explanation
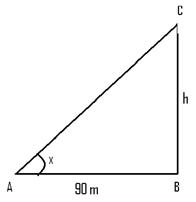
Let cot-1(4/5) = x => cotx = 4/5 => tan(x) = 5/4 From the right angled triangle Tan(x) = h/90 => h = 5/4*90 =112.5 m
Q 3 - On the level ground, the angle of elevation of the top of a tower is 30°.on moving 20 meters nearer, the angle of elevation is 45°.Then the height of the tower is
Answer - C
Explanation
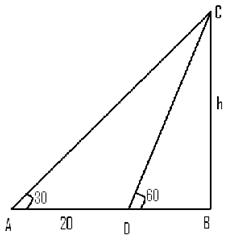
Let h be the height of tower From figure. 20 =h ( cot30 - cot60) 20 =h (â3-1/â3) => 20â3 = h (3-1) => h=10â3.
Q 4 - The angles of elevation of the tops of two vertical towers as seen from the middle point of the lines joining the foot of the towers are 45° & 60°.The ratio of the height of the towers is
Answer - B
Explanation
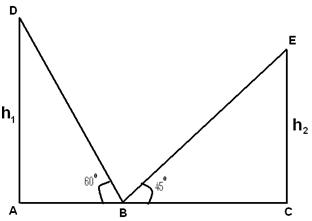
Tan(60)=h1/AB => h1=â3AB Tan(45)=h1/BC => h2=BC h1/ h2=â3/1 => h1:h2=â3:1
Q 5 - The heights of two towers are 90 meters and 45 meters. The line joining their tops make an angle 450 with the horizontal then the distance between the two towers is
Answer - B
Explanation
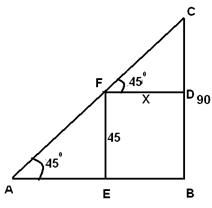
Let the distance between the towers be X From the right angled triangle CFD Tan(45)= (90-45)/X => x=45 meters
Q 6 - From a point P on a level ground, the angle of elevation of the top tower is 60°. If the tower is 180 m high, the distance of point P from the foot of the tower is
Answer - A
Explanation
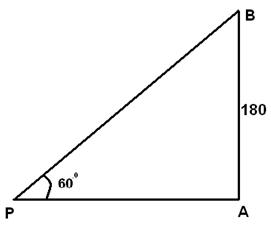
From â APB = 60° and AB = 180 m. AB/AP= tan 60° =â3 AP=AB/â3 =180/â3=60â3
Q 7 - The Top of a 25 meter high tower makes an angle of elevation of 450 with the bottom of an electric pole and angle of elevation of 30 degree with the top of pole. Find the height of the electric pole.
Answer - B
Explanation
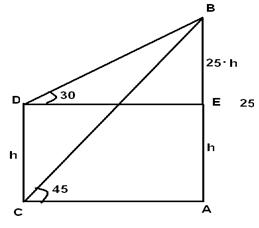
Let AB be the tower and CD be the electric pole. From the figure CA = DE => 25/(Tan(45))=(25-h)/(Tan(30)) => 25 Tan(30) = 25-h => h=25-25Tan(30) =25(1- Tan(30)) =25((â3-1)/â3)
Q 8 - An observer 1.4 m tall is 10â3 away from a tower. The angle of elevation from his eye to the top of the tower is 60°. The heights of the tower is
Answer - D
Explanation
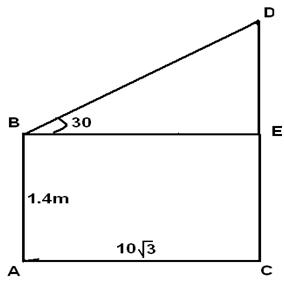
Let AB be the observer and CD be the tower. Then, CE = AB = 1.4 m, BE = AC = 10v3 m. DE/BE=Tan (30) =1/â3 DE=10â3/â3=10 CD=CE+DE=1.4+10=11.4 m
Q 9 - A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 60° with the man's eye when at a distance of 75 meters from the tower. After 10 seconds the angle of depression becomes 45°. What is the approximate speed of the boat, assuming that it is running in still water?
Answer - D
Explanation
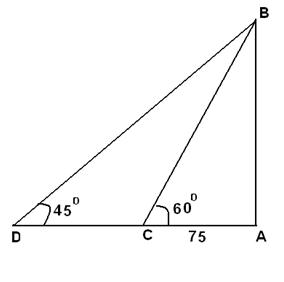
Let AB be the tower and C and D be the positions of the boat. Distance travelled by boat = CD From the figure 75tan(60)=(75+CD)tan(45) =>75â3 = 75+CD =>CD =55 m Speed = distance/time=55/10 =5.5 m/sec=19.8 kmph
Q 10 - The horizontal distance between two towers is 90 m. The angular depression of the top of the first as seen from the top of the second which is 180 m high is 450.Then the height of the first is
Answer - C
Explanation
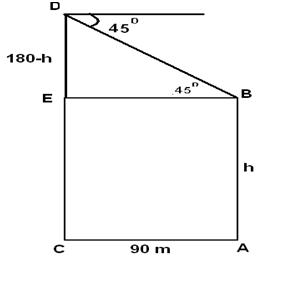
=>(180-h)/90 = Tan(45) => h =90 m