- Aptitude - Home
- Aptitude - Overview
- Quantitative Aptitude
Geometry - Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Geometry. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

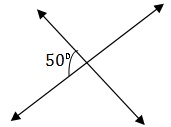
Q 1 - Two Lines AB and CD intersect at O. If ∠AOC =50⁰,Then ∠ BOD and ∠AOD are respectively
Answer : B
Explanation
∠ BOD=∠ AOC (vert . opp. ∠s) =50⁰ ∠AOC +∠AOD = 180⁰ ⇒ 50⁰ +∠AOD= 180⁰ ⇒∠AOD=130⁰ ∴ ∠ BOD= 50⁰ and ∠AOD = 130⁰.
Answer : A
Explanation
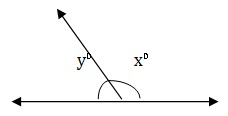
x+y = 180 ⇒ x+ 4/5 x = 180 ⇒ 5x +4x = 900 ⇒ 9x=900 ⇒ x = 100.
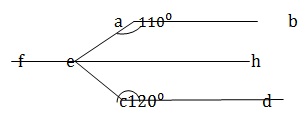
Q 3 - In the given figure , AB || CD, ∠BAE =110⁰ , ∠ECD = 120⁰ and ∠AEC =x⁰. Then, x= ?
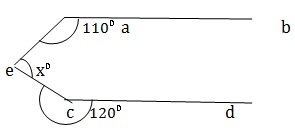
Answer : A
Explanation
Draw FEG∥ AB ∥CD. AB∥ EG and AE is the transversal. ∴ ∠BAE +∠AEG = 180⁰ ⇒ 110⁰ + ∠AEG =180⁰ ⇒ ∠AEG =70⁰ Again, EG∥ CD and EC is transcersal. ∴ ∠GEC + ∠ ECD = 180⁰ ⇒ ∠GEC +120⁰ =180⁰ ⇒ ∠GEC= 60⁰ ∴ X= 70+60 =130
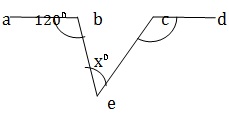
Q 4 - In the given figure , AB ll CD, ∠ABE =120⁰, ∠DCE = 100⁰ and ∠BEC =x⁰. Then, x= ?
Answer : C
Explanation
Through E draw GEH ∥ AB ∥CD AB∥ EG and BE is the transversal. ∠ ABE +∠ GEB = 180⁰ ⇒ 120⁰ +∠GEB =180⁰ ⇒ ∠GEB = 60⁰ CD ∥EH and CE is the transversal. ∴∠DCE +∠CEH = 180⁰ ⇒ 100⁰ + ∠CEH =180⁰ ⇒ CEH = 80⁰ NOW ∠GEB+ ∠BEC +∠CEH = 180⁰ ⇒ 60+x+80 =180 ⇒ x = 40
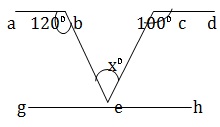
Answer : B
Explanation
∠ A- ∠B = 33⁰ and ∠B -∠C =18⁰ ⇒ A= 33+ B and C=B -18 = (33+B) + B + (B-18) =180 ⇒ 3B =165 ⇒ B 55. ∴ ∠B =55⁰.
Q 6 - Two poles of heights 6m and 11m stand vertically on a plane ground. If the distance between their feet is 12m , what is the distance between their tops?
Answer : A
Explanation
Let AB and CD be the poles such that AB = 6m , CD = 11 m and BD =12m Draw AE ⊥ CD . Then , AE = BD = 12m CE = CD - DE = CD - AB = (11 - 6) m =5m. from right AEC we have AC2 = AE2 + CE2 = (12)2 + 52 = (114 +25)=169 ⇒ Ac = √169 = 13m ∴ Distance between their tops= 13m

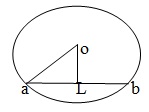
Q 7 - A chord of length 30cm is at a distance of 8cm from the center of a circle . The radius of the circle is
Answer : D
Explanation
Let O be the centre of the circle and AB be the chord. Draw OL ⊥ AB. Then AL= 1/2 AB = (1/2 *30)cm =15 cm and OL = 8cm. OA2 = OL2 +AL2= 82 + (15)2 = (64 + 225 ) =289 ⇒ OA = √289 = 17cm. ∴ Radius of the circle is 17 cm.
Q 8 - In the given figure , O is the center of a circle and arc ABC subtends an angle of 130⁰ at O. AB is extended to P. Then ∠PBC= ?
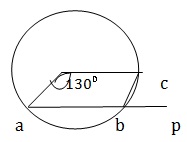
Answer : C
Explanation
Take a point D on the remaining part of circumference of the circle. Join DA and DC ∠ADC = 1/2 ∠AOC = 1/2 *130⁰ = 65⁰. Now DABC is a cyclic quadrilateral. &There4; ∠ADC + ∠ABC = 180⁰⇒ 65⁰+ ∠ABC = 180⁰ ⇒ ∠ABC = 115⁰. ⇒∠ PBC= (180⁰ - 115⁰) =65⁰.
Q 9 - In the given figure, AOB is a diameter of the circle and CD || AB. If ∠DAB = 25⁰ ,Then ∠CAD=?
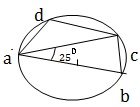
Answer : B
Explanation
AB DC and AC is a transversal. ∴ ∠ACD = ∠CAB = 25⁰ (alt. s ) ∠ACB = 90⁰ ( angle in a semicircle) ∴ ∠BCD =∠ACB + ∠ ACD=(90⁰ +25⁰)= 115⁰. ∠BAD + ∠BCD = 180⁰ ⇒ ∠BAC +∠CAD +∠BCD = 180⁰ ⇒ 25⁰ +∠ CAD + 115⁰ =180⁰ ⇒ ∠CAD = 40⁰
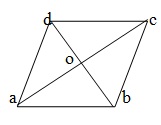
Q 10 - The lengths of the diagonals of a rhombus are 24cm and 18cm respectively. The length of each side of the rhombus is
Answer : C
Explanation
Let ABCD be a rhombus in which diagonal AC=24 cm and diagonal BD =18 cm . We know that the diagonal of a rhombus bisect each other at right angle. ∴ OA = 1/2 AC =(1/2 *24 ) cm =12cm OB = 1/2 BD = (1/2 *18 ) cm =9cm AB2 = OA2 + OB2 = (12) 2 + 92 = (144 +81) = 225 ⇒ AB = √225 = 15 cm. ∴ Each side of the rhombus is 15 cm.