What is the Halting Problem in TOC?

Usually, programs consist of loops that are limited or unlimited in length.

The total work done by the program completely depends on the input given to the program.

The program may consist of several different numbers of loops that may be in linear or nested manner.

The Halting Problem is the problem of deciding or concluding based on a given arbitrary computer program and its input, whether that program will stop executing or run-in an infinite loop for the given input.

The Halting Problem tells that it is not easy to write a computer program that executes in the limited time that is capable of deciding whether a program halts for an input.

In addition to that the Halting Problem never says that it is not practicable to determine whether a given random program is going to halt (stop).

Generally, it asks the question like “Given a random program and an input, conclude whether the given random program is going to halt when that input is given”.

Write a Halting Problem

An example of writing the Halting Problem is as follows −

INPUT − Program P and a string S.

OUTPUT − if P stops on S, it returns 1.

Otherwise, if P enters into an endless loop on S, it returns 0.

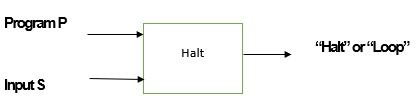
Let us consider the Halting Problem called H having the solution.

Now H takes the following two inputs −

• Program P

• Input S.

If P stops on S, then H results in “halt”, otherwise H gives the result “loop”.

The diagrammatic representation of H is as follows −

Example

ATM = {(M,w) | M is a TM and M halts at input w }.

We can build a universal Turing machine which can simulate any Turing machine on any input.

Let’s consider TM which recognizing the Altering Turing Machine (ATM) −

Recognize-ATM (<M,w>)
   Simulate M using UTM till it halts
   If M halts and accept then
      Accept
   Else
      Reject

Suppose, if M goes into an infinite loop on input w, then the TM Recognize-ATM is going to run forever which means TM is only a recognizer, not a decider.

A decider for this problem would call a halt to simulations that loop forever.

Now the question is whether an ATM is TM decidable is equivalent to asking the question whether we can tell if a TM M will halt on input w.

Because of this, both versions of this question are generally called the halting problem.