Pumping Lemma for Regular Expression

---

---

In this chapter, we will explain one of the most important concepts in automata theory which is a little bit puzzling too; it is the concept of pumping lemma. Pumping lemma can be used for regular languages and context free languages.

Here most importantly, we will see the regular languages and pumping lemma on it. For the context, let's start with the regular languages then jump to the pumping lemma with examples for a better understanding.

What are Regular Languages?

We have crossed a long journey on regular languages. For a recap, regular languages are a special kind of language that can be recognized by a finite automaton. Think of a finite automaton as a machine with a finite memory. It reads symbols from an input string one at a time and uses its limited memory to decide whether the string belongs to the language.

For example, consider the language of all strings over the alphabet {a, b} that end with 'aa'. This language is regular because we can construct a finite automaton with two states: one for the initial state and another for a state that indicates the presence of 'aa'.

Why Do We Need the Pumping Lemma?

The pumping lemma is a way to prove that a language is not regular. It provides a powerful way to show that no finite automaton can recognize a language, even if we can't explicitly construct one.

The lemma essentially states that if a language is regular, then any sufficiently long string in the language can be pumped meaning a substring can be repeated an arbitrary number of times, and the resulting string will still be in the language.

It is little bit confusing. Let us see the lemma first and then understand through example.

The Steps for Pumping Lemma

Let's break down the pumping lemma step-by-step −

Step 1: Consider a language as regular

To begin with this lemma, we start by assuming that the language we want to analyse is regular. This assumption will eventually lead to a contradiction if the language is indeed not regular.

Step 2: Assume a constant C and select a string W

We need to select a constant 'C' and a string 'W' from the language. Now the string 'W' should have a length greater than or equal to the constant 'C'. Here this constant 'C' represents the maximum number of states in a hypothetical finite automaton that recognizes the language.

Step 3: Divide the string W into three substrings X, Y, and Z

We need to split the string 'W' into three parts, namely 'X', 'Y', and 'Z'. The important condition here is that the length of the substring 'Y' should be greater than zero. So that 'Y' must contain at least one symbol. We also need to make sure that the combined length of 'X' and 'Y' is less than or equal to the constant 'C'.

Step 4: Pump the substring Y

The most important part of the pumping lemma is that we can repeat the substring 'Y' any number of times, and the resulting string will still belong to the language. So it means that we can create new strings by taking the original string 'W' and replacing the 'Y' substring with 'Y' repeated 'i' times, where 'i' is any non-negative integer. The resulting string will be of the form 'XYⁱ Z', where Y^i represents the substring 'Y' repeated 'i' times.

Step 5: The contradiction

If, for any choice of 'W', 'X', 'Y', and 'Z' satisfying the conditions mentioned above, we can find a value of 'i' for which the string XYⁱ Z does not belong to the language, then our initial assumption that the language is regular must be false.

Let us see an example that what we have covered here.

Example of Pumping Lemma for Regular Expression

Suppose we have a language, L = {aⁿ bⁿ | n >= 1}. This language consists of strings with an equal number of 'a's and 'b's, with at least one 'a' and one 'b'. Just apply the above steps inside this.

• Consider a language as regular − We start by assuming that L is a regular language.
• Assume a constant C and select a string W − Let's choose the constant C = 3 and the string W = "aaa bbb" (n = 3). The length of W is 6, which is greater than C.
• Divide the string W into three substrings X, Y, and Z − We can divide W into X = "aa", Y = "a", and Z = " bbb". Notice that the length of Y is 1, which is greater than zero, and the length of X Y is 3, which is less than or equal to C.
• Pump the substring Y − Now, let's try pumping the substring Y. If we repeat Y once, we get the string "aa a bbb" (n = 4), which is still in the language. However, if we repeat Y twice, we get the string "aa aa bbb" (n = 5), which is not in the language.
• The contradiction − Since we found a value of 'i' (i = 2) for which the string ' XY^i Z ' does not belong to the language, our initial assumption that L is regular must be false.

If we try to make the FSM, it will be like −

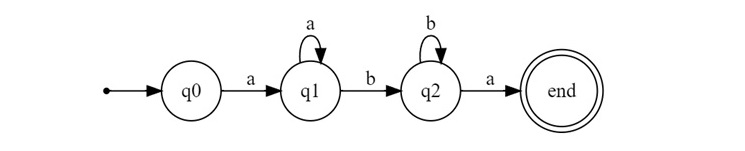
This finite automaton can accept strings with an equal number of 'a's and 'b's. However, it cannot remember the exact count of 'a's and 'b's.

When pumping the substring 'Y' (in our example, 'a'), the automaton loses track of the number of 'a's, leading to an imbalance in the number of 'a's and 'b's, thus creating a string that doesn't belong to the language. This demonstrates the limitation of a finite automaton and why L cannot be recognized by one.

Conclusion

In this chapter, we explained the concept of finite automata in regular expressions. The pumping lemma is a fundamental tool in automata theory. It is used to prove that a language is not regular, even without constructing a finite automaton.