
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Finite Sets and Infinite Sets
Read this chapter to learn the concepts of finite and infinite sets, their definitions, and properties. Finite sets are countable and contain a finite number of elements, while infinite sets are not finite and extend to infinity. Examples of countable infinite sets include rational numbers.
We encounter both finite and infinite sets in our daily lives, and this chapter aims to provide a better understanding of their differences using examples. It will also provide examples to illustrate the differences between finite and infinite sets.
What is Finite Sets?
Finite sets, also known as countable sets, have a finite number of elements that can be counted. They end with a starting and ending element. These sets can be represented in roster notation form, such as the set of vowels in the English alphabets V = {a, e, I, o, u}, which has a finite number of elements.
All finite sets are countable, but not all countable sets are finite. For instance, set for a set with odd natural numbers less than 19, and A = {3, 5, 7, 9, 11} it is a valid set with 5 elements which is countable.
Some of properties of finite sets are listed below:
- We can get a proper subset of a finite set which is also finite.
- The union of any finite sets is also finite.
- The intersection of two finite sets is also finite.
- The cartesian product of finite sets is finite.
- The cardinality of a finite signifies finite number and it is equal to the number of elements in that set.
- Similarly, the power set of a finite set is also finite.
What is Infinite Sets?
Infinite sets are not finite, meaning their elements are infinite. They are infinite from start to end or both sides have continuity. Examples include the set of whole numbers and the set of real numbers. These sets are uncountable and their elements are represented by dots: W = {0, 1, 2, 3, ..}, representing the infinity of the set. The set of whole numbers is an example of an infinite set.
An infinite set has an element count that is infinite, value that we are unable to pinpoint the precise number of elements. On the other hand, countable infinite sets have countable element counts. One such example is the set of integers Z = { -2, -1, 0, 1, 2, .}, which has an infinite element count and whose elements can be put in a one-to-one correspondence with the set of natural numbers.
Some of the important properties of infinite sets include the following −
- The union of any infinite sets is also infinite set.
- The power set of infinite set is also infinite.
- The superset of an infinite set returns infinite set.
- Sometimes a subset of an infinite set is finite or sometimes infinite.
- Infinite sets can be both countable and uncountable.
Venn Diagram of Finite Sets and Infinite Sets
As we know, a Venn diagram is used to represent relationships among sets or groups of objects. The following figure shows the relationship between finite and infinite sets.
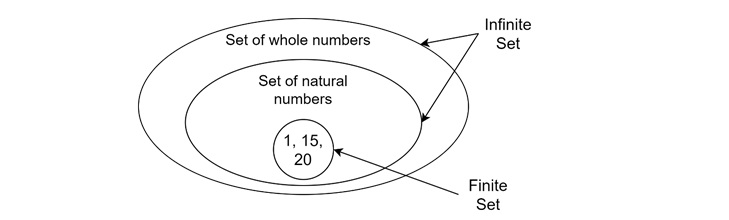
A finite set consists of elements 1, 15, and 20, while an infinite set consists of natural numbers and whole numbers. Multiple finite sets can be created from an infinite set, as seen in the example of a finite set lying inside an infinite set.
Difference between Finite Sets and Infinite Sets
The following table compares and contrasts the features of Finite and Infinite Sets −
| Finite Sets | Infinite Sets |
|---|---|
| Finite sets are countable number of elements | There are infinitely many elements in infinite set. |
| If two finite sets are merged, they will become finite. | If two infinite or one finite one infinite sets are merged they become infinite. |
| Subset of a finite set is also finite. | Subset of infinite set is sometimes finite sometimes infinite. |
| The power set of a finite set is finite. | The power set of infinite is also infinite. |
Conclusion
In this chapter, we explained the concepts of finite sets and infinite sets. Finite sets have elements that we can count, whereas infinite sets have elements we cannot count because they have infinitely many elements.
We described the properties with examples along with the differences and Venn diagram for a better understanding.