Two-stack Pushdown Automata

---

---

So far, in this tutorial, we have come across context-free grammars (CFG) and pushdown automata (PDA) to accept the CFG. But PDA or CFG have certain limitations; they cannot handle any type of language. For that reason, we jump to more advanced machines.

A little complex and advanced machine than pushdown automata is two-stack pushdown automata. In this chapter, we will have a look at two-stack pushdown automata with examples for a better understanding.

Why Do We Need Complex Machines over One-stack Pushdown Automata

We are very much familiar with this concept.

• Finite automata can recognize regular languages. An example is $\mathrm{\{a^{n}\:|\: n \: \geq \:0\}}$
• Pushdown automata (PDA) can recognize context-free languages. An example $\mathrm{\{a^{n}b^{n}\:|\: n \: \geq \:0\}}$.
• But what about more complex languages like $\mathrm{\{a^{n}b^{n}c^{n}\:|\: n \: \geq \:0\}?}$ Our regular PDA gets stuck here.

This is where our two-stack PDA comes to the consideration.

What is a Two-stack Pushdown Automata?

A two-stack PDA is like a more powerful version of PDA. The properties are written below −

• It has not one, but two stacks for storage.
• It can be deterministic, meaning it always knows what to do next.
• It can recognize all context-free languages, whether they're deterministic or not.
• It can even handle some context-sensitive languages, like $\mathrm{\{a^{n}b^{n}c^{n}\:|\: n \: \geq \:0\}}$

Components of Two-stack Pushdown Automata

A two-stack PDA is defined by a 9-tuple: M = (Q, Σ, Γ, Γ', δ, q0, z1, z2, F)

• Q − All the states the PDA can be in
• Σ − The input alphabet (symbols it can read)
• Γ − The alphabet for the first stack
• Γ' − The alphabet for the second stack
• δ − Rules for moving between states and using the stacks
• q0 − The starting state
• z1 − The bottom symbol for the first stack
• z2 − The bottom symbol for the second stack
• F − The final or accepting states

How Does a Two-stack Pushdown Automata Work?

The transition function δ is the main thing in automata. Here for two-stack PDA as well. It looks like this −

$$\mathrm{Q\:\times\:(\Sigma\:\cup\:\{\lambda\})\:\times\:\Gamma\:\times\:\Gamma'\:\rightarrow\:(Q,\:\Gamma,\:\Gamma')}$$

This indicates −

• It considers the current state, the input symbol (or for no input), and the top symbols of both stacks.
• Based on these, it decides the next state and what to do with both stacks.

Let us see examples for a better understanding −

Example: Recognizing $\mathrm{\{a^{n}b^{n}c^{n}\:|\: n \: \geq \:0\}}$

Let's see how a two-stack PDA can handle the $\mathrm{\{a^{n}b^{n}c^{n}\:|\: n \: \geq \:0\}}$. This language has equal numbers of a's, b's, and c's in that order.

Strategy

Here's how we'll use our two stacks −

• While reading 'a', we'll push 'X' into stack 1.
• While reading 'b', we'll push 'Y' into stack 2.
• While reading 'c', we'll pop 'X' from stack 1 and 'Y' from stack 2.
• If both stacks are empty at the end, we accept the string.

Transition Functions

$$\mathrm{\delta(q0, \: \lambda, \: z1, \: z2) \: \rightarrow \: (qf, \: z1, \: z2)}$$

$$\mathrm{\delta(q0, \: a, \: z1, \: z2) \: \rightarrow \: (q0, \: Xz1, \: z2)}$$

$$\mathrm{\delta(q0, \: a, \: X, \: z2) \: \rightarrow \: (q0, \: XX, \: z2)}$$

$$\mathrm{\delta(q0, \: b, \: X, \: z2) \: \rightarrow \: (q0, \: X, \: Yz2)}$$

$$\mathrm{\delta(q0, \: b, \: X, \: Y) \: \rightarrow \: (q0, \: X, \: YY)}$$

$$\mathrm{\delta(q0, \: c, \: X, \: Y) \: \rightarrow \: (q1, \: \lambda, \: \lambda)}$$

$$\mathrm{\delta(q1, \: c, \: X, \: Y) \: \rightarrow \: (q1, \: \lambda, \: \lambda)}$$

$$\mathrm{\delta(q1, \: \lambda, \: z1, \: z2) \: \rightarrow \: (qf, \: z1, \: z2)}$$

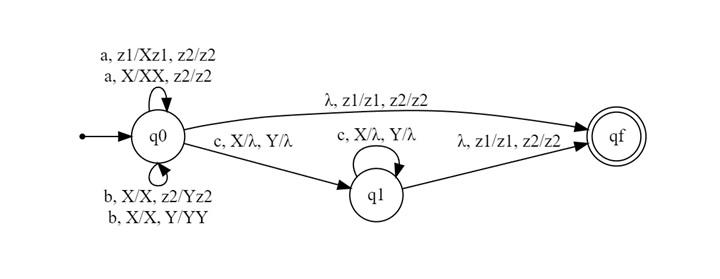
Explanation of Transitions

• The first line handles the case of an empty input string.
• The next two lines handle reading 'a' and pushing 'X' to stack 1.
• The fourth and fifth lines handle reading 'b' and pushing 'Y' to stack 2.
• The sixth and seventh lines handle reading 'c' and popping from both stacks.
• The last line checks if we have finished the string with empty stacks.

Why two-stack PDA is more powerful?

• They can recognize all context-free languages, just like regular PDAs.
• They can also recognize some context-sensitive languages, which regular PDAs can't.
• In fact, two-stack PDAs are equivalent to Turing machines! This means they can compute anything that's computable.
• This equivalence is proven by something called Minsky's theorem.

Conclusion

Two-stack Pushdown Automata are a powerful than normal one-stack pushdown automata. In this chapter, we explained the concept of two-stack pushdown automata with examples where we have three symbols at the same time. We also presented transition diagrams for easy understanding. A two-stack pushdown automaton is much advanced so that it is equivalent to Turing machines.