
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Undecidable Languages in Automata Theory
In this chapter, we will explain the concept of "undecidable languages" in the context of "Turing machines" and "computability". In the previous chapters, we have covered the Church-Turing Thesis and Recursively Enumerable languages. Here, we will recap the basics of "decidability" and recursively enumerable languages, as these concepts are important for understanding the overall concept of "undecidability".
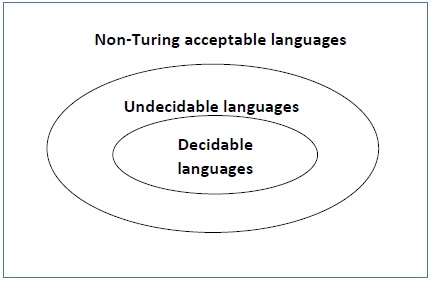
Decidable Languages
A language L is said to be decidable if there exists a Turing machine that can always decide whether any given string belongs to L or not. In simpler terms, if we pass a string to this Turing machine, it will always halt, giving a clear answer: either it will accept the string (if the string is in the language) or reject it (if the string is not in the language).
Recursive Languages
Decidable languages are closely related to recursive languages. A language is recursive if there exists a Turing machine that will accept all the strings in L and reject all the strings that are not in L.
The key point here is that the Turing machine will always halt, no matter what input is given. This is the characteristic feature of recursive languages, making them a subset of decidable languages.
Recursively Enumerable Languages
Next, let us get the idea in brief on recursively enumerable languages. A language L is said to be recursively enumerable if there exists a Turing machine that will accept and halt for all input strings that are in L.
However, for strings that are not in L, the Turing machine may or may not halt. This means that while the machine will always halt and accept for strings in the language, it may go into an infinite loop for strings not in the language.
Partially Decidable Languages
Recursively enumerable languages are also known as partially decidable languages. This is because the Turing machine will sometimes halt (when the string is in the language) and sometimes it will not halt (when the string is not in the language).
The key difference between recursive languages and recursively enumerable languages is that in recursive languages, the Turing machine always halts, while in recursively enumerable languages, halting is not guaranteed for strings outside the language.
Undecidable Languages
The language is said to be undecidable when it is not decidable. In other words, there is no Turing machine that can decide every string in the language, meaning the Turing machine cannot always halt with a decision.
Characteristics of Undecidable Languages
An undecidable language might be partially decidable, meaning there could be a Turing machine that accepts some strings in the language and halts, but this machine will not halt for some strings outside the language.
However, there are also languages that are not even partially decidable. For these languages, there is no Turing machine that can reliably decide whether a string belongs to the language or not. Such languages have no corresponding Turing machine that can recognize them.
Example of an Undecidable Problem: The Halting Problem
The Halting Problem checks whether a given Turing machine will halt when given a particular input or not. There is no general algorithm (and therefore no Turing machine) that can solve the halting problem for all possible Turing machines and inputs.
The halting problem can be formalized as a language LH, where −
$$\mathrm{L_H \:=\: \{ \langle M,\: w \rangle\: \mid\: M\: \text{ is a Turing machine and }\: M \:\text{ halts on input }\: w \}}$$
Here, $\mathrm{\langle M,\: w \rangle}$ represents the encoding of a Turing machine M and an input string w. The halting problem asks if there is a Turing machine that can decide whether M halts on w. Turing proved that such a Turing machine cannot exist, meaning that LH is undecidable.
Summarizing the Concepts
The following table summarizes the key concepts that we have covered so far in this chapter −
| Type of Language | Description | Turing Machine Behavior |
|---|---|---|
| Recursive Languages | Languages for which a Turing machine will always halt, either accepting or rejecting each input. | Turing machine always halts, either accepts or rejects. |
| Recursively Enumerable Languages (Partially Decidable) | Languages for which a Turing machine will halt if the string is in the language, but may not halt if it is not. | Turing machine halts when it accepts; may loop infinitely if it does not. |
| Undecidable Languages | Languages for which no Turing machine exists that can decide all strings in the language. | No Turing machine can decide the language; may not halt for some inputs. |
What Does Undecidability Signify?
Recursive languages are those where the Turing machine always halts, providing a clear decision. Recursively enumerable languages are less predictable, with the Turing machine sometimes halting and sometimes not, depending on the input.
Undecidable languages take this unpredictability further. They represent problems that cannot be solved by any algorithm or Turing machine, such as the halting problem.
The lack of a Turing machine to solve these languages states the limitations of computation. It is showing that there are questions computers cannot answer.
Conclusion
In this chapter, we presented the concept of Undecidable Languages and their relation with Turing Machine. We have seen the recursively enumerable and recursive languages in short to understand the concept of "undecidability" better.