
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Finite Automata Exercises
Question 1
Design a two-input, two-output sequence detector that generates an output '1' every time the sequence 1011 is detected. Overlapping sequences should also be counted. Draw the state table and the state diagram.
Solution
We want to detect sequence: 1011
States and Transitions
- S1: Initial state. If input is 0, stay in S1 with output 0. If input is 1, move to S2 with output 0.
- S2: If input is 0, move to S3 with output 0. If input is 1, stay in S2 with output 0.
- S3: If input is 0, return to S1 with output 0. If input is 1, move to S4 with output 0.
- S4: If input is 0, return to S1 with output 0. If input is 1, move to S2 with output 1 (sequence detected).
The sequence 1011 is a sequence that requires a starting point from S1. If input 0 is not received, the sequence is confined in S1, producing output 0. If input 1 is received, the sequence is confined in S2, producing output 0.
If input 1 is received, the sequence is confined in S3, producing output 0. If input 0 is received, the sequence is confined in S1, producing output 0. If input 011 is received, the sequence detector can produce 1.
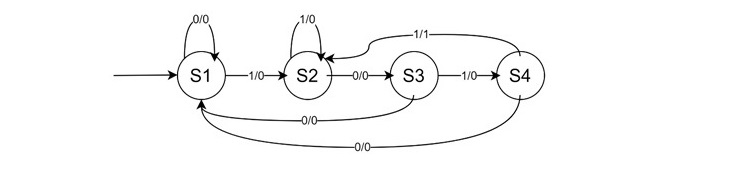
Here is its State Table −
| Present State | Input 0 | Input 1 |
|---|---|---|
| S1 | S1, Output 0 | S2, Output 0 |
| S2 | S3, Output 0 | S2, Output 0 |
| S3 | S1, Output 0 | S4, Output 0 |
| S4 | S1, Output 0 | S2, Output 1 |
Question 2
Design a two-input, two-output sequence detector that generates an output '1' every time the sequence 10101 is detected. Overlapping sequences should also be counted. Draw the state table and the state diagram.
Solution
We want to detect sequence: 10101
States and Transitions
- S1: Initial state. If input is 0, stay in S1 with output 0. If input is 1, move to S2 with output 0.
- S2: If input is 0, move to S3 with output 0. If input is 1, stay in S2 with output 0.
- S3: If input is 0, move to S4 with output 0. If input is 1, move to S1 with output 0.
- S4: If input is 0, move to S5 with output 0. If input is 1, move to S2 with output 0.
- S5: If input is 0, return to S1 with output 0. If input is 1, move to S2 with output 1 (sequence detected).
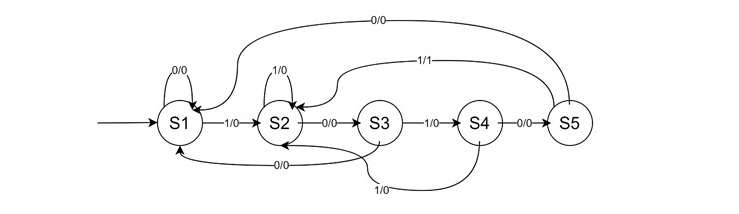
Here is its State Table −
| Present State | Input 0 | Input 1 |
|---|---|---|
| S1 | S1, Output 0 | S2, Output 0 |
| S2 | S3, Output 0 | S2, Output 0 |
| S3 | S4, Output 0 | S1, Output 0 |
| S4 | S5, Output 0 | S2, Output 0 |
| S5 | S1, Output 0 | S2, Output 1 |
Question 3
Find the equivalent partition for the following machine −
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| A | B | 0 | C | 1 |
| B | A | 0 | E | 1 |
| C | D | 1 | E | 1 |
| D | E | 1 | B | 1 |
| E | D | 1 | B | 1 |
Solution
For a string with no input, all states are 0-equivalent, with P0 = (ABCDE). For string length 1, there are two input types: 0 and 1, with states A and B giving output 0 and states C, D, and E giving output 1. Thus, states in set P0 are divided into (AB) and (C, D, E), with P1 = ((AB) (CDE).
For input string length 1, A and E are distinct because they produce different outputs. For input string length 2, the distinguishability is determined by the next state combination. States A and B produce next states B and A, and next states C and E for input 1. B and A belong to the same set, and C and E also belong to the same set. AB cannot be partitioned for input string length 2. The set (CDE) is partitioned into (C) and (DE), and the new partition becomes P2= ((AB) ((C) (DE)).
For input string length 3, the same process is performed, with states A and B producing next states B and A, and next states C and E for input 1. C is a single state and cannot be partitioned further. States D and E produce next states E and D, respectively, for input 0, and B and E belong to the same set, so D and E cannot be divided. The new partition becomes P3= (A)(B)(C)(DE).
To check for input string length 4, three subsets contain single states A, B, and C, which cannot be partitioned further. States D and E produce the next states E and D for input 0 and B for input 1, respectively. D and E belong to the same set, and their partition is the same as P3, making P3 the equivalent partition of the machine.
After minimization
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| S1(A) | S2 | 0 | S3 | 1 |
| S2(B) | S1 | 0 | S4 | 1 |
| S3(C) | S4 | 1 | S4 | 1 |
| S4(D,E) | S4 | 1 | S2 | 1 |
Question 4
Simplify the following incompletely specified machine −
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| A | B | 0 | D | 1 |
| B | D | 1 | F | 1 |
| C | F | 1 | B | 1 |
| D | F | 0 | A | 1 |
| E | C | 0 | A | 1 |
| F | C | 1 | B | 1 |
Solution
The partitions are −
- P0 = (ABCDEF)
- P1 = (ADE)(BCF) (Depending on output for input 0)
- P2 = (ADE)(B)(CF) (For input 0, the next state of B goes to another set)
- P3 = (A)(DE)(B)(CF) (For input 0, the next state of A goes to another set)
- P4 = (A)(DE)(B)(CF)
As P3 and P4 are the same, P3 is the equivalent partition.
The unique equivalent partition, P4, represents the minimized machine's state. To simplify, we can rename the partitions (A, B, DE, and CF) as S1, S2, S3, and S4, respectively, to simplify the process.
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| S1(A) | S2 | 0 | S3 | 1 |
| S2(B) | S3 | 1 | S4 | 1 |
| S3(C, D) | S4 | 0 | S1 | 1 |
| S4(E, F) | S4 | 1 | S2 | 1 |
Question 5
Test whether the following machine is finite or not −
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| A | C | 1 | D | 0 |
| B | D | 1 | E | 0 |
| C | B | 1 | E | 1 |
| D | B | 1 | A | 0 |
| E | D | 1 | B | 1 |
Solution
The partitions are −
- P0 = (ABCDEF)
- P1 = (AD)(BCE) (Depending on output for input 1)
- P2 = (AD)(BE)(C) (For input 0, the next state of C goes to another set)
- P3 = (A)(D)(BE)(C) (For input 0, the next state of A and D goes to a different set)
- P4 = (A)(D)(BE)(C)
From here, we can see P3 and P4 are same, so P3 is equivalent partition.
The unique equivalent partition, P4, represents the minimized machine's state. To simplify, we can rename the partitions (A, BE, C, and D) as S1, S2, S3, and S4, respectively, to simplify the process.
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| S1(A) | S3 | 1 | S4 | 1 |
| S2(B,E) | S4 | 1 | S2 | 0 |
| S3(C) | S2 | 1 | S2 | 1 |
| S4(D) | S2 | 1 | S1 | 0 |
Question 6
Minimize the following incompletely specified machine −
| Present State | Next State (z) | |||||
|---|---|---|---|---|---|---|
| I1 | I2 | I3 | ||||
| A | D | 1 | E | 1 | - | - |
| B | B | 0 | E | - | C | - |
| C | C | - | C | 0 | B | - |
| D | B | 0 | D | - | E | - |
| E | - | - | B | 0 | A | - |
Solution
We can introduce temporary state T that is placed in the next state where the next states are not specified, and no output is required. As a temporary state T is considered, T is put in the present state with the next state T for all inputs with no output.
| Present State | Next State (z) | |||||
|---|---|---|---|---|---|---|
| I1 | I2 | I3 | ||||
| A | D | 1 | E | 1 | T | - |
| B | B | 0 | E | - | C | - |
| C | C | - | C | 0 | B | - |
| D | B | 0 | D | - | E | - |
| E | T | - | B | 0 | A | - |
| T | T | 0 | T | 0 | T | 0 |
Question 7
Construct a compatible graph for the following incompletely specified machine −
| Present State | Next State (z) | |||||
|---|---|---|---|---|---|---|
| I1 | I2 | I3 | ||||
| A | A | 1 | D | - | C | - |
| B | A | - | D | - | E | - |
| C | E | 0 | A | 1 | - | - |
| D | E | - | A | 1 | - | - |
| E | E | 0 | - | - | C | - |
Solution
Incompletely specified machines lack all next states or outputs. To minimize these machines, we use the merger graph and compatible graph method. From the merger graph, we find compatible pairs and construct a compatible graph. From the compatible graph, we find the closed partition, which are the minimized states of the machine.
The machine has five states, and its merger graph consists of five nodes: A, B, C, D, and E. The outputs of A and B do not differ, creating an arc between them. The next state conflicts, creating an interrupted arc.
The next state pairs (CE) are placed in the interrupted portion. A and C have no arc between them, and C and D have an uninterrupted arc between them. The merger graph is constructed, crossing the arcs between A, E, and (AD), BE, BD, and BC.
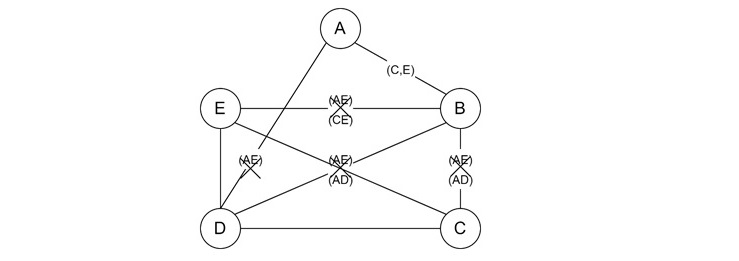
Next, we need to consider the compatibility graph, where the graph consists of four vertices (AB, CD, DE), and (CE), with a closed covering for the machine if all outgoing edges and terminal vertices belong to the subgraph. The minimized machine states are (AB) and (CDE).
To create a closed covering, rename (AB) as S1 and (CDE) as S2, and draw a directed arc from (AB) to (CE). This ensures that every state of the machine is covered by at least one vertex.
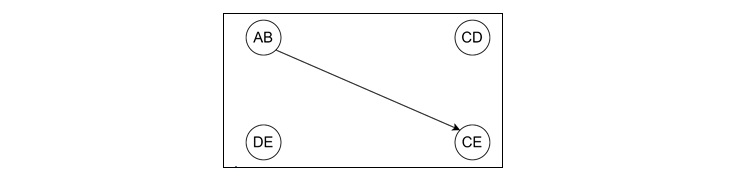
So, the minimized machine is −
| Present State | Next State (z) | |||||
|---|---|---|---|---|---|---|
| I1 | I2 | I3 | ||||
| S1 | S1 | 1 | S2 | - | S1 | - |
| S2 | S2 | 0 | S1 | 1 | S2 | - |
Question 8
Check whether the following machine is finite or not −
| Present State | Next State (z) | |||
|---|---|---|---|---|
| I1 | I2 | |||
| A | A | 0 | B | 1 |
| B | C | 0 | D | 1 |
| C | B | 1 | A | 0 |
| D | D | 1 | C | 0 |
Solution
The Testing Table-Testing Graph Method involves creating a divided table with two halves for a machine with two inputs and two outputs.
The upper half contains single state input-output combinations, while the lower half contains two state combinations. Six combination pairs are formed, resulting in a total of four states.
| Present State | 0/0 | 0/1 | 1/0 | 1/1 |
|---|---|---|---|---|
| A | A | - | - | B |
| B | C | - | - | D |
| C | - | B | A | - |
| D | - | D | C | - |
| AB | AC | - | - | BD |
| AC | - | - | - | - |
| AD | - | - | - | - |
| BC | - | - | - | - |
| BD | - | - | - | - |
| CD | - | BD | AC | - |
The testing table contains six present state combinations and six nodes, each labelled with an input output combination. The testing graph for finite memory is a directed arc from SiSj [i≠ j] to SpSq [p≠ q], where Sp and Sq is the implied pair of SiSj.
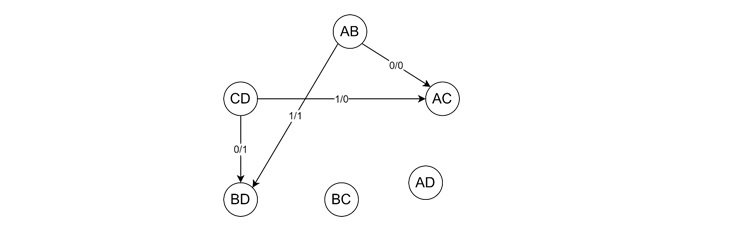
The testing graph is loop-free, indicating a finite machine. The longest path is 1, and the order of finiteness is 1+1 = 2. This can be proven using the vanishing connection matrix method.
The connection matrix consists of six rows and columns, labelled with present state combinations. The (i, j)th entry in the matrix is 1 if there is an entry in the corresponding testing table, otherwise, it is 0.
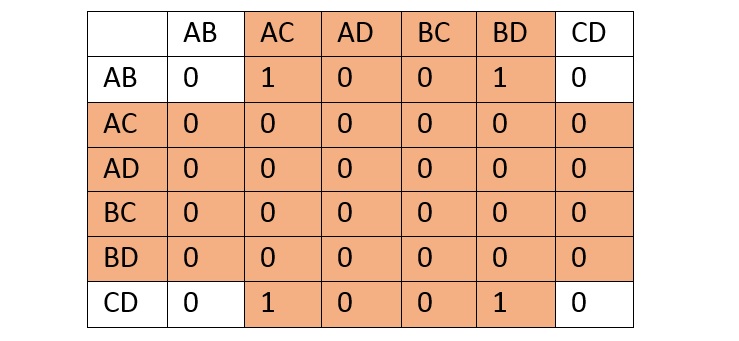
Consider the red marked are crossed. The matrix contains all '0' rows AC, AD, BC, and BD, resulting in the corresponding columns and rows labelled AC, AD, BC, and BD disappearing.
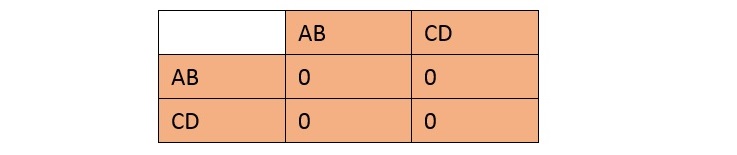
The matrix contains '0' rows AB and CD, causing the columns to vanish. The number of steps required to do so is 2, indicating the machine's order of finiteness is 2.
Question 9
Check whether the following machine is information lossless or not. If lossless, find its order.
| Present State | Next State (z) | |||
|---|---|---|---|---|
| X = 0 | X = 1 | |||
| A | B | 1 | A | 1 |
| B | D | 0 | B | 0 |
| C | D | 0 | B | 1 |
| D | E | 1 | C | 1 |
| E | A | 1 | B | 0 |
Solution
To determine if a machine is lossless, construct a testing table, which should be divided into two halves.
| Present State | Next State | |||
|---|---|---|---|---|
| Z = 0 | Z = 1 | |||
| A | - | AB | ||
| B | BD | - | ||
| C | D | B | ||
| D | - | CE | ||
| E | B | A | ||
| AB | - | - | ||
| BD | - | - | ||
| CE | BD | AB | ||
The testing table does not contain any repeated entry, so the machine is an information lossless machine.

The testing graph for information loss lessness is loop-free. The order of lossless-ness is m = 1 + 2 = 3. The length of the longest path of the graph is 1.
Question 10
Consider the following DFA, then find the number of strings of length 8 will be accepted by the DFA.
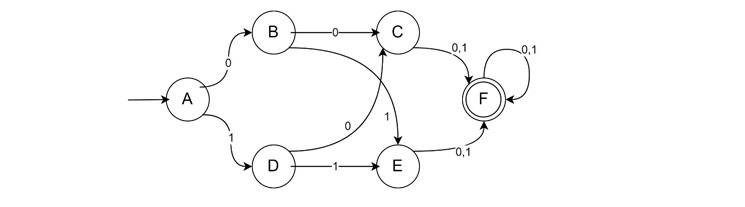
Solution
With all possible strings of length three on set {0, 1}, we can achieve the end state. The ultimate state can be reached in eight different ways. After that, there will be a five-length string with two possible outcomes for each of the five positions: 0 or 1.
Thus, 8 * 25 = 28 = 256 will be the total number of strings approved.