Derivation Tree in Automata Theory

---

---

In automata theory, we use derivation trees or parse trees to derive language from grammars. In this chapter, we will see the concept of derivation trees in the context of context-free-grammars. Derivation tree is a fundamental tool in understanding and representing the structure of strings generated by context-free grammars.

What are Derivation Tree?

A Derivation Tree, also known as a Parse Tree, is a visual representation of the process by which a context-free grammar generates a particular string. It provides a hierarchical breakdown of the string. This illustrates the sequence of production rules applied to derive the string from the grammar's start symbol.

Key Elements of a Derivation Tree

Before learning how to construct a derivation tree, let's understand their essential components:

• Root Vertex − The root vertex represents the starting point of the derivation process and is always labeled with the grammar's start symbol.
• Vertices (Internal Nodes) − These nodes represent the non-terminal symbols of the grammar, serving as intermediate stages in the derivation.
• Leaves − These nodes represent the terminal symbols of the grammar, forming the final string derived from the grammar. They can also be labeled with the empty symbol, ε, if the grammar allows for empty productions.

Example of Context-Free Grammar

Let's consider the following context-free grammar G −

$$\mathrm{G \:=\: (V,\: T,\: P,\: S)}$$

Where,

• V = {S, A, B} (Variables or Non-terminal symbols)
• T = {0, 1} (Terminal symbols)
• P = {S → 0B, A → 1AA | ε, B → 0AA} (Production Rules)
• S = S (Start Symbol)

This grammar defines a language where strings begin with a '0', then followed by a combination of '0's and '1's.

Derivation Tree Construction

To illustrate the formation of a derivation tree, let us examine the derivation of the string "001" from the grammar G:

Root Vertex

We begin by placing the start symbol 'S' as the root vertex of the tree.

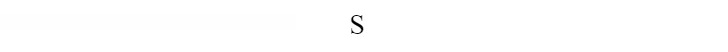
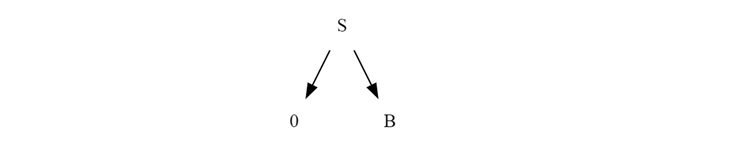
Applying Production Rules

Looking at the production rules, we see that 'S' can be replaced by "0B".

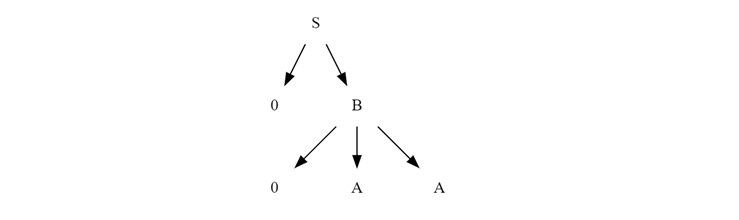
Continuing the Derivation

The rightmost vertex is 'B', and the production rule for 'B' is "0AA". Applying this rule, we obtain −

Reaching Terminal Symbols

Now, we have two 'A' variables. Since the production rule for 'A' allows for the empty string 'ε', we can replace the right most 'A's with 'ε', and left A to 1AA.

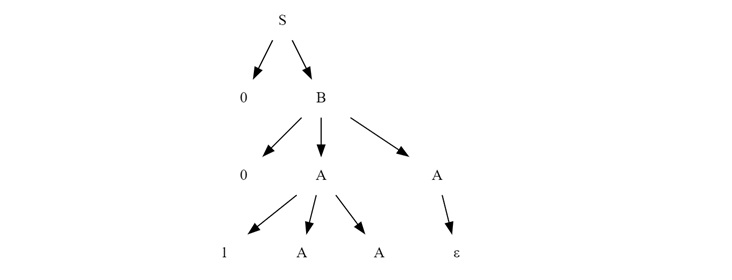
Now from the final non-terminals A to ε to get final tree.

This final structure represents the derivation tree for the string "001" from grammar G.

Left Derivation Tree and Right Derivation Tree

There are two primary methods for constructing derivation trees: The left derivation and right derivation. These methods dictate the order in which production rules are applied to non-terminal symbols within the sentential form.

• Left Derivation Tree − A Left Derivation Tree is generated by consistently applying production rules to the leftmost variable in each step of the derivation. This method uses expanding the non-terminal symbols on the left side of the sentential form.
• Right Derivation Tree − A Right Derivation Tree is obtained by applying production rules to the rightmost variable in each step. This method uses expanding non-terminal symbols on the right side of the sentential form.

Example of Left and Right Derivation Trees

Let's consider a new grammar and generate both left and right derivation trees to understand the difference in their construction.

Grammar −

$$\mathrm{S \: \rightarrow \: aAS | aSS | ε}$$

$$\mathrm{A \: \rightarrow \: SbA | ba}$$

$$\mathrm{\text{String to derive: "aabbaa"}}$$

Left Derivation Tree

For the left derivation tree, we start from S.

• Applying Leftmost Derivation − We apply the production rule 'S → aSS' to the leftmost 'S'.

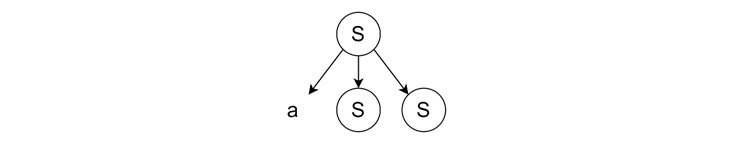
• Expanding Leftmost Variable − We expand the leftmost 'S' using the rule 'S → aAS'.

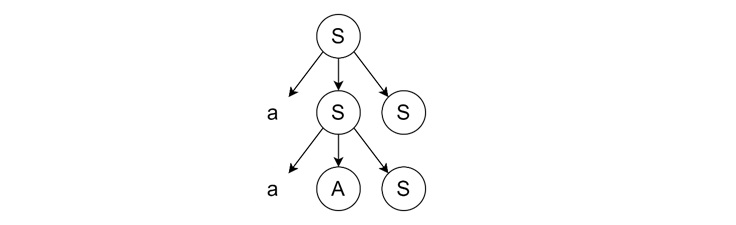
• Continuing Leftmost Derivation − We continue expanding the leftmost 'A' using the rule 'A → ba'.

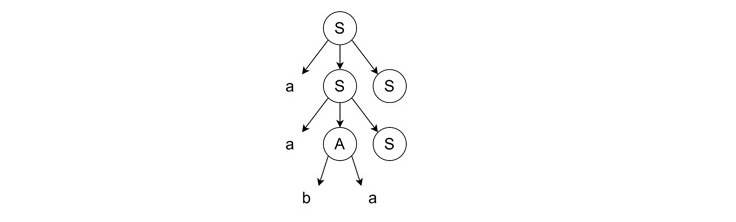
• Completing the Derivation − We expand the next leftmost S to aSS, and from there remaining S to 'S → ε'.

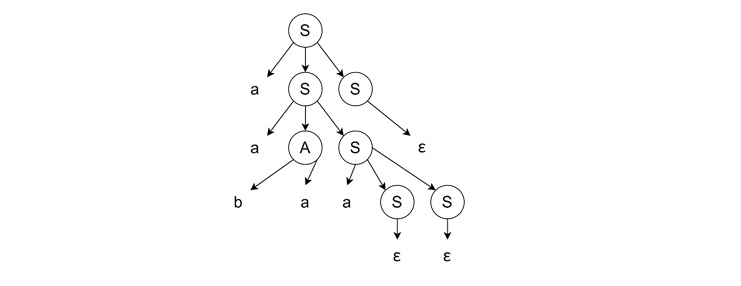
Right Derivation Tree

Like left most derivation, we start from the start symbol 'S'.

• Applying Rightmost Derivation − We apply the production rule 'S → aSS' to the rightmost 'S'.

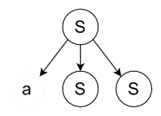
• Expanding Rightmost Variable − We expand the rightmost 'S' using the rule 'S → aAS'.

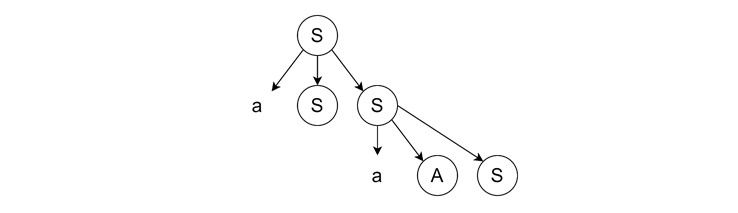
• Continuing Rightmost Derivation − We expand the rightmost 'S' using the rule 'S → aSS'.

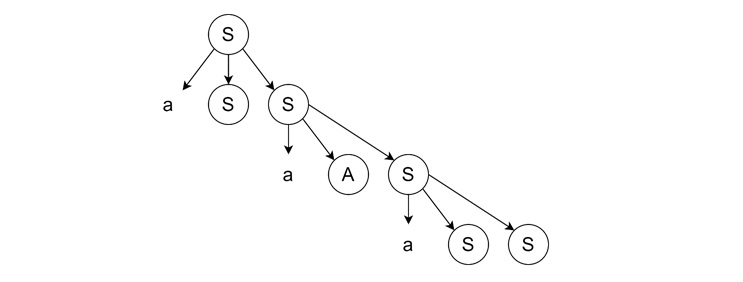
• Completing the Derivation − We expand the remaining 'A' and 'S' from the right to left, the last two S will produce ε. Then A will bring ‘ba’ and the leftmost S will bring ε again.

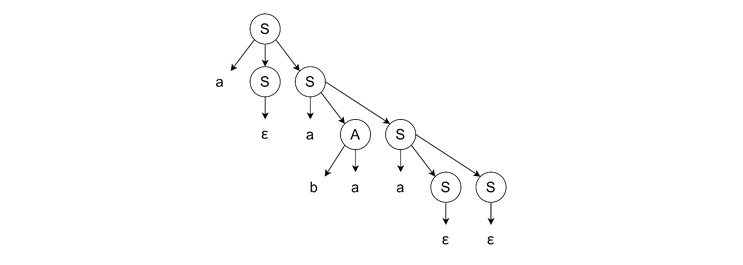
Conclusion

Derivation trees provide a method of visualizing the structure of strings generated by context-free grammars. These are essential in several cases including understanding the concepts CFG derivation, parsing in compiler design, etc. In this chapter, we explained the concepts in detail with step by step examples for a clear understanding.