Multi-head Turing Machine in Automata Theory

Quiz

A standard Turing machine has a single read-write head that interacts with an infinitely long tape. However, there is a variation of Turing machine that features multiple read-write heads on a single tape, allowing it to perform tasks more efficiently by processing multiple parts of the tape simultaneously. It is called a multi-head Turing machine.

In this chapter, we will explore the concept of Multi-head Turing Machine in detail with examples for a better understanding.

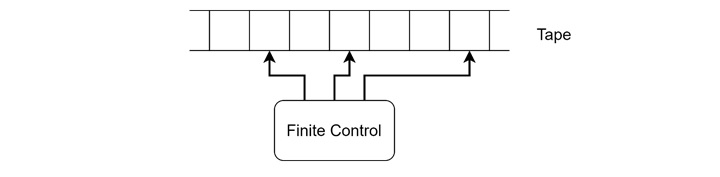
Basics of Multi-head Turing Machine

A Multi-head Turing Machine is similar to the standard Turing machine but with an important modification −

It has multiple heads instead of just one.
These heads are connected to a single finite control unit, which directs the machine's operations.
Each head can read and write symbols independently, enabling the machine to perform more complex operations in parallel.

The functional block diagram of the machine is looking like below −

Key Characteristics of Multi-head Turing Machines

Let us see some of the important characteristics of the multi-head Turing machines −

Multiple Heads − The Turing machine can have several read-write heads, each of which can move independently across the tape.
Single Tape − Unlike the multi-tape Turing machine, the multi-head Turing machine still operates on a single tape.
Transition Function − The transition function in a multi-head Turing machine is more complex. It takes into account the symbols under each head and determines the next state, the symbols to write, and the movements of each head.

Why Use Multiple Heads?

Why do we have to use multi-head Turing Machines? The primary advantage of using multiple heads is that it allows the machine to process different parts of the tape simultaneously. This can significantly reduce the time complexity of certain computational tasks, making the multi-head Turing machine more efficient than its single-head counterpart.

How Does a Multi-head Turing Machine Work?

In a multi-head Turing machine, each head operates independently but is controlled by the same finite control. The transition function defines how the machine reacts based on the current state and the symbols read by all the heads.

Transition Function

The transition function for a multi-head Turing machine can be expressed as −

$$\mathrm{\delta(Q,\: \Sigma_{1},\: \Sigma_{2},\: \dotso,\: \Sigma_{n})\: \rightarrow\: (Q,\: (\Gamma_{1} \:\times\: \{L,\: R,\: N\} ),\: (\Gamma_{2}\: \times\: \{L,\: R,\: N\}),\: \dotso,\: (\Gamma_{n} \:\times\: \{L,\: R,\: N\}))}$$

Where,

Q is the current state.
Σ₁, Σ₂, …, Σ_n are the symbols read by each head.
Γ₁, Γ₂, …, Γ_n are the symbols to be written by each head.
L, R, N indicate the direction of movement (Left, Right, No movement) for each head.

Handling Conflicts

Two special cases need to be handled carefully −

Multiple Heads on the Same Cell − If more than one head is positioned on the same tape cell and they attempt to write different symbols, the machine must have a predefined priority among the heads. The head with the highest priority determines the final symbol written.
Leftmost Cell Movement − If a head is at the leftmost position on the tape and is instructed to move left, the machine must handle this condition to prevent what is known as "hanging."

Example of Checking for a Palindrome

Let us see how a multi-head Turing machine can be used to check whether a binary string is a palindrome or not. As we know a palindrome is a string that reads the same forward and backward, such as "1001" or "101"

To start the work, we need to set it up first −

Consider a multi-head Turing machine with two heads, H₁ and H₂.
Head H₁ starts at the leftmost end of the string, and head H₂ starts at the rightmost end.
The machine's goal is to compare corresponding symbols from both ends of the string moving toward the center.

Initial Configuration

The string is written on the tape, and both heads are positioned at opposite ends of the string. The machine starts in an initial state q0.

First Comparison

The heads H₁ and H₂ read the symbols under them. If the symbols are the same (both '0' or both '1'), the machine moves both heads inward (right for H₁ and left for H₂), replacing the symbols with a blank ('B').

Subsequent Comparisons

This process continues, with each head moving inward and comparing symbols until one of two conditions is met −

Condition 1 − Both heads read a blank symbol ('B'). This indicates that all corresponding symbols matched, and the string is a palindrome. The machine transitions to an accepting state.
Condition 2 − The symbols do not match. This means the string is not a palindrome, and the machine transitions to a rejecting state.

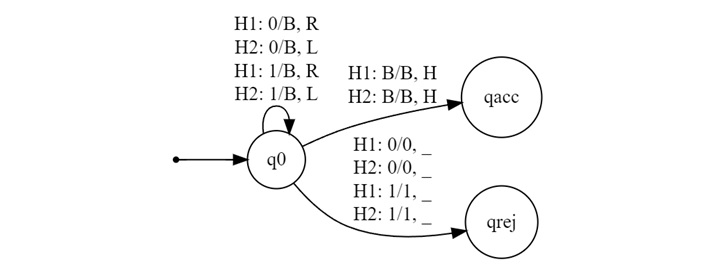
Example for String "1001"

Let's see how the machine processes the string "1001" −

Step 1 − The heads start at the first and last positions of the string. Both read '1'. The machine replaces them with 'B' and moves the heads inward.
Step 2 − The heads now read '0' at both positions. Again, the machine replaces them with 'B' and moves inward.
Step 3 − Both heads now read 'B', indicating the string has been fully processed. The machine enters the accepting state, confirming that "1001" is a palindrome.

Example for String "101": For the string "101"

Step 1 − The heads start at the first and last positions of the string, reading '1'. The machine replaces them with 'B' and moves inward.
Step 2 − Both heads read '0', which are identical. The machine moves inward again.
Step 3 − Both heads now read 'B', so the machine enters the accepting state, confirming that "101" is also a palindrome.

Equivalence to Single-head Turing Machine

A multi-head Turing machine, can be converted to an equivalent single-head Turing machine. This conversion is possible by simulating the working of multiple heads on a single tape. However, the process is more complex and less efficient than using multiple heads directly.

Simulating Multiple Heads − Each head's position and the symbol it reads are tracked on a single tape. The single-head machine mimics the actions of all heads by sequentially processing their tasks.
Resulting Efficiency − While this proves that multi-head Turing machines have no more computational power than a single-head Turing machine, the multi-head machine can perform certain tasks much faster.

Conclusion

In this chapter, we presented the concept of multi-head Turing machine which is powerful than the single-head machines. Here we explained the concept with an example and its steps with state transition diagrams. A multi-head Turning machine is highly in solving complex problems.

Print Page