Reducibility in Automata Theory

Quiz

Reduction refers to the process of converting one problem into another, already solved problem, in such a way that the solution to the latter can help solve the former. Let us see the idea through basic concepts and examples for a clear understanding.

Basics of Reducibility

The concept of reducibility involves two problems −

One that is already solved and
Another that we want to solve.

Let us denote these problems as A and B, where B is the solved problem. The process of reduction allows us to use the solution to B to solve A.

Let's characterize Reducibility −

Solving A is not harder than solving B − If A can be reduced to B, then solving A cannot be more complex than solving B. This is because B is already a solved problem, and we use its solution to address A.
Decidability through reduction − If A is reducible to B and B is a decidable problem, then A is also decidable. This means that if we know how to solve B in a finite number of steps, we can apply the same method to solve A.
Undecidability and reduction − If A is an undecidable problem and can be reduced to B, then B is also undecidable. This property is interesting when proving that certain problems are undecidable by showing that they can be reduced to a known undecidable problem.

The Membership Problem

The membership problem checks whether a given string w is accepted by a Turing machine M or not. To understand the undecidability of this problem, assume for a moment that it is decidable. If so, there must be a Turing machine A_TM that takes <M, w> as input and halts, accepting if M accepts w, and halts, rejecting if M rejects w.

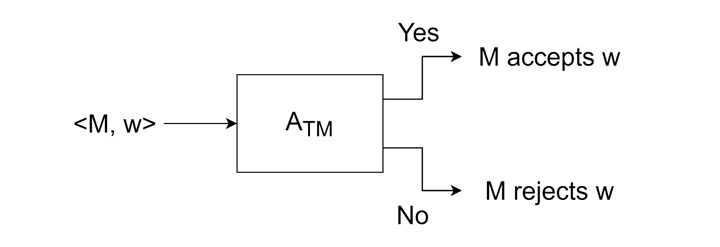
However, by reducing the problem of recognizing a Turing-acceptable language to this membership problem, a contradiction arises. We know that some Turing-acceptable languages are undecidable, and assuming the membership problem is decidable leads us to incorrectly conclude that all such languages are decidable. This contradiction proves that the membership problem is undecidable.

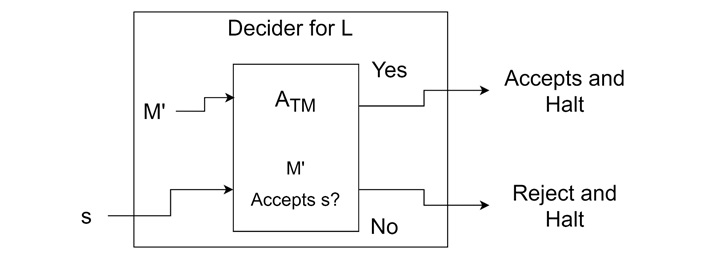
Let L be a recursively enumerable language and M' be the TM accepting L. Let us design a decider for L reducing it to A_TM. The pair <M', s> is given as input to A_TM, where s is a string. As A_TM is the general TM for the arbitrary string w given input to the arbitrary TM M, it will halt for every input. Thus, L is decidable.

From here, it is proved that every Turing-acceptable language is decidable. But already, it is proved that there is a Turing-acceptable language which is undecidable. So, we get a contradiction. Our assumption is wrong.

The Halting Problem

Another interesting problem in is the halting problem. The problem is to determine whether a Turing machine M will halt when run on a specific input www. Assume that this problem is decidable, implying the existence of a Turing machine A_TM that decides whether M halts on w.

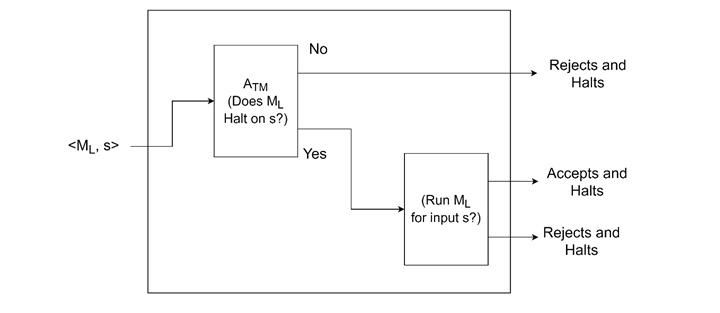
To prove undecidability, we can reduce the halting problem to another problem by constructing a new Turing machine M′ based on M. M' writes the input www on its tape and then behaves like M.

If M halts on w, then M' halts; otherwise, M' does not halt. Since we know that the halting problem is undecidable, any problem to which it is reduced must also be undecidable. Hence, the halting problem itself is undecidable.

The Blank Tape Halting Problem

The blank tape halting problem considers whether a Turing machine MMM halts when started with a blank tape. We can prove this problem's undecidability by reducing the halting problem to it.

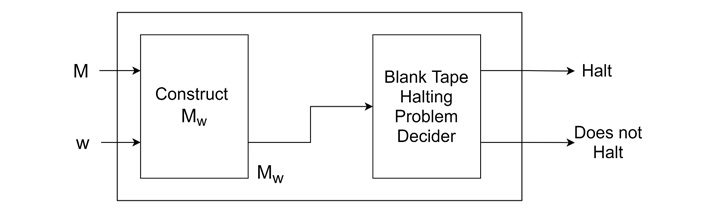
Suppose that the blank tape halting problem is decidable. This implies the existence of a decider that halts and accepts if M halts with a blank tape and halts and rejects otherwise.

By constructing a machine M' from M that starts with a blank tape, writes the input w, and then simulates M, we can reduce the halting problem to the blank tape halting problem. Since the halting problem is undecidable, the blank tape halting problem must also be undecidable.

Regular Language Acceptance Problem

Next, another problem is whether a Turing machine M accepts a regular language or not. If this problem were decidable, we could use a decider that halts and accepts if w is a regular language and halts and rejects otherwise.

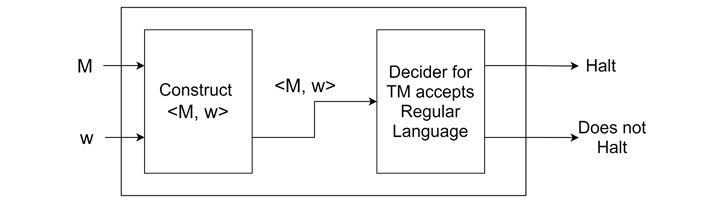
By reducing the halting problem to this problem, we construct a machine M' such that if M does not accept w, the decider accepts a non-regular language, and if M accepts w, it accepts the regular language Σ^*. The reduction shows that if the regular language acceptance problem were decidable, the halting problem would be as well. Since the halting problem is undecidable, the regular language acceptance problem is also undecidable.

The Language Emptiness Problem

The language emptiness problem is another such problem, which checks whether a given Turing machine M generates an empty language or not. If this problem were decidable, a decider would exist and that halts and accepts if M generates an empty language and halts and rejects otherwise.

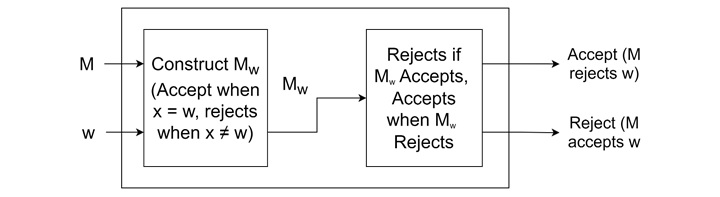
To prove undecidability, we reduce the halting problem to this problem by constructing a machine M_w that accepts a language if and only if w is in the language recognized by M. If w is not accepted by M, then the decider accepts the non-empty language generated by M_w. If w is accepted, the decider generates an empty language. Since the halting problem is undecidable, the language emptiness problem must also be undecidable.

Conclusion

In this chapter, we explained the concept of reducibility in computation theory. Starting with the basics of reducibility and its properties, we presented several examples including the membership problem, halting problem, blank tape halting problem, regular language acceptance problem, and language emptiness problem. Through these examples, we highlighted how reducibility is used to prove the undecidability of various problems.

Print Page