
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Transition Table in Automata Theory
In the very basic discussion of automata theory, we talk about state diagrams or state-transition diagrams to visually represent a machine or automata. Another representation of the same is transition tables which are nothing but the same representation in a tabular form.
In this chapter, we will cover the transition tables in detail including how they are formed, their properties, and applications.
A Little Background on Automata
Before discussing the concept of transitions in automata, we must understand the background. In computer science, automata is a fundamental branch which deals with abstract machines and the problems they can solve.
We know the automaton is a mathematical model of a computing device that can be used to recognize patterns within input data. There are mainly two things involved in automata.
- States − These represent the different configurations or conditions of an automaton, or what actions the automaton can do.
- Transitions − These define how the automaton moves from one state to another based on the input that state consumed.
If we talk about the finite state automaton, we mostly focus −
- Deterministic Finite Automata (DFA) − In a DFA, for each state and input symbol, there is exactly one transition to a next state.
- Non-deterministic Finite Automata (NFA) − An NFA allows multiple transitions from a state for a given input symbol, including the possibility of no transition.
A little variation of FSM is the Pushdown Automata (PDA), which is nothing but an FSM with additional stack data-structure.
Transition and Transition Table
Consider the following state diagram along with the transition table −

In this finite state machine, there are four states. The initial state is q1 and the final state is qf. There are several transitions from one state to another. However, not all state has all possible transitions, and for a single input it is moving more than one states. So this is an example of non-deterministic FSM. Let us see the corresponding transition table for this same state diagram.
| Present State | Next State | |
|---|---|---|
| 0 | 1 | |
| q1 | q2, q3 | - |
| q2 | - | q1, q3 |
| q3 | - | qf |
| qf | - | - |
The table shows the states and for which symbol it will jump to which state. This transition tables are equivalent to the state transition diagrams to represent an automaton.
Let us see another example with inputs and outputs −
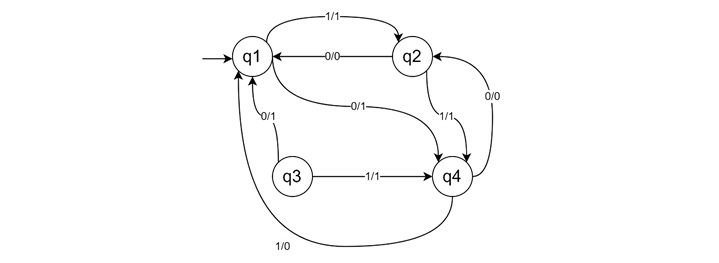
Here we have 4 states but there is no final state since this automaton is making output while transitioning. On the arc, we have input and output separated by the "/" symbol. The corresponding transition table will be look like the following −
| Present State | Next State | |||
|---|---|---|---|---|
| Input: 0 | Input: 1 | |||
| State | Output | State | Output | |
| q1 | q4 | 1 | q2 | 1 |
| q2 | q1 | 0 | q4 | 1 |
| q3 | q1 | 1 | q4 | 1 |
| q4 | q2 | 0 | q1 | 0 |
Advantages of Transition Tables
Transition Tables provide a clear and concise way to visualize the state transitions based on different input symbols.
- Purpose − Transition tables are crucial for comprehending, analyzing, and designing automata by visualizing their behavior, determining language acceptance, and converting between representations like state diagrams.
-
Components − A transition table typically consists of −
- States − A list of all possible states the automaton can be in.
- Input symbols − The set of symbols the automaton can process.
- Next states − The state the automaton transitions to based on the current state and input symbol.
- Transition tables are versatile tools for analyzing automata behavior. Some possible advantages of using them are −
- Simulating automata − By starting at the initial state and following the transitions based on the input string, one can simulate the automaton's execution.
- Determining language acceptance − An automaton accepts a string if it reaches an accepting state after processing the entire input. Transition tables help in tracing this process.
- Converting to other representations − Transition tables can be easily converted to state diagrams, which provide a visual representation of the automaton.
Conclusion
Transition tables are crucial in automata theory, providing a structured representation of automaton behavior. They are essential for understanding, designing, and analyzing automata.
In this chapter, we explained the specific types of automata (DFA, NFA, PDA) and covered the concept of transition diagram and transition tables.