Variations of Turing Machine in Automata Theory

---

---

Turing machines are powerful computational models that can simulate any algorithmic process. A standard Turing machine consists of a single tape and a single read-write head. However, there are variations of Turing machine that have been developed to address different computational challenges. These variations differ mainly in structure and operation, but they all have the same computational power as the standard Turing machine.

In this chapter, we will present an overview of these different types of Turing machines with diagrams for a better understanding.

Multi-tape Turing Machine

As the name suggests, a multi-tape Turing machine is an extension of the standard Turing machine where multiple tapes are available for input, output, and computation. Each tape has its own read-write head, and the machine's transition function is based on the current state and the symbols read by each head.

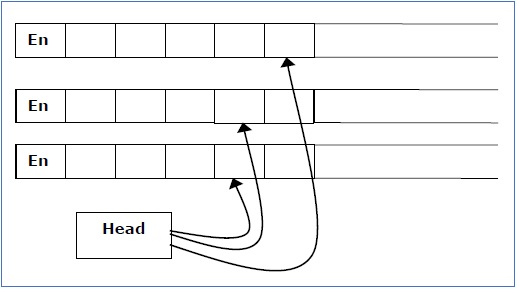
Example

Consider the problem of checking if a binary string is a palindrome or not. A two-tape Turing machine can solve this by copying the string from the first tape to the second, then comparing the string on both tapes in opposite directions.

The process involves copying input from one tape to another, tracing the first tape from left to right while moving the second tape from left to right, and comparing symbols. If all corresponding symbols match, the string is a palindrome, reducing time complexity compared to a single-tape machine.

Multi-head Turing Machine

In a multi-head Turing machine, a single tape is used, but it has multiple read-write heads. These heads can independently read and write symbols, enabling the machine to perform complex tasks more efficiently.

Example

The same palindrome checking can be done with this also. The heads start at both ends of the string and move towards each other, checking if the corresponding symbols are identical.

• If multiple heads attempt to write different symbols to the same cell, a priority system determines which head's action is executed.
• If a head tries to move left beyond the leftmost cell, a special condition known as "hanging" occurs, which needs to be handled.
• The multi-head Turing machine, like the multi-tape machine, can be converted to an equivalent single-head machine, although the process may be more complex.

Two-way Infinite Tape Turing Machine

A two-way infinite tape Turing machine allows the tape to extend infinitely in both directions, unlike the standard machine where the tape extends infinitely in only one direction. This removes the boundary on the left side of the tape.

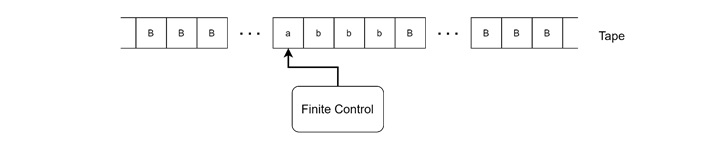
Benefits

This variation can be particularly useful in computations where data may need to be processed symmetrically around a central point.

It can be simulated by a standard Turing machine by marking the left boundary and preventing the head from moving beyond it.

K-dimensional Turing Machine

A K-dimensional Turing machine extends the concept of the tape to multiple dimensions. For example, a two-dimensional Turing machine as given in the following diagram, has a tape that extends infinitely in both the X and Y directions.

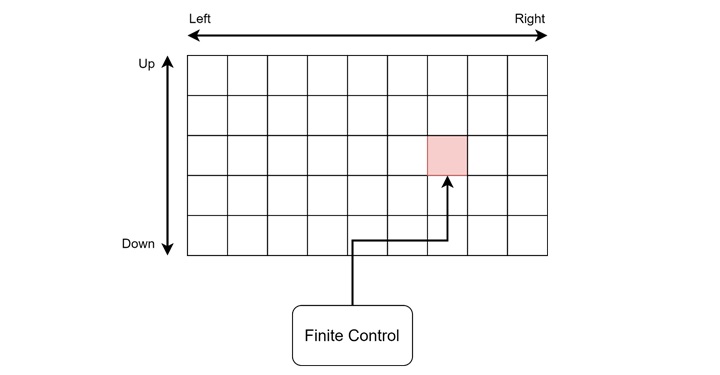
In a two-dimensional Turing machine, the read-write head can move not only left and right but also up and down. This added flexibility allows the machine to process more complex data structures, such as matrices or grids. This type of Turing machine is ideal for tasks that naturally fit a multi-dimensional space, such as image processing or simulations of physical phenomena.

Non-deterministic Turing Machine

A non-deterministic Turing machine (NDTM) differs from a deterministic Turing machine in that it can transition into multiple possible states from a given state and symbol. Instead of following a single path, the NDTM can explore many computational paths simultaneously.

Example

Consider the language L = {0ⁿ 1^m} where n and m are not necessarily equal. An NDTM can non-deterministically choose how many 0's and 1's to match, accepting the string if it satisfies the condition.

Every non-deterministic Turing machine has an equivalent deterministic Turing machine. The deterministic version simulates all possible paths of the NDTM and accepts the string if any path leads to an accepting state.

Enumerator Turing Machine

An enumerator Turing machine is designed to generate strings of a language. It is equipped with a work tape and an output tape. The machine writes symbols to the output tape, which is then printed.

The enumerator repeatedly writes symbols on the output tape based on its transition functions. Once a string is completed, it is printed, and the machine resets to generate the next string.

This type of Turing machine is useful for tasks where the goal is to list all valid strings of a language, such as generating all possible solutions to a problem.

Conclusion

Turing machines, in all their variations, are built due to the flexibility and power of computational models. Whether it's the parallel processing capabilities of multi-tape and multi-head machines, the extended reach of infinite tape machines, or the exploratory nature of non-deterministic machines, each variant has its strengths and weaknesses. Through these variations, Turing Machines can solve a large variation of problems efficiently.