Convert Regular Grammar to Finite Automata

---

---

In the last chapter, we covered how to convert finite automata to regular grammar. In this chapter, we will understand the steps to convert a regular grammar to finite automata.

The process of converting a regular grammar containing epsilon productions into a finite automata is not a complex process. Here we will see the steps involved, covering the crucial step of eliminating epsilon productions before constructing the automata. We will also have an example to get a better understanding of the concept.

Understanding Epsilon Productions

As we know the null production or epsilon productions are a key concept in formal language theory. An epsilon production in a grammar is a production of the form A → ε, where 'A' is a non-terminal symbol, and 'ε' represents the empty string (a string with no symbols).

These productions can pose a challenge when converting a grammar into a finite automata, as they introduce the potential for empty transitions.

The Need for Epsilon-Free Grammars

Finite automata, by definition, operate on strings of symbols. They cannot directly handle transitions that involve the empty string. So, before we can convert a grammar containing epsilon productions into a finite automata, we need to eliminate these productions.

Eliminating Epsilon Productions: A Step-by-Step Approach

Let's see the process of converting a regular grammar with epsilon productions to an epsilon-free grammar using a concrete example. Consider the following grammar −

S → a, aA | bB 
A → aA | aS 
B → cS 
S → ε 
B → ε 

Step 1: Identifying Epsilon Productions

First, we identify the epsilon productions in our grammar. In this case, they are −

S → ε 
B → ε

Step 2: Generating Non-Epsilon Productions

We list all the productions that do not involve epsilon. These are the productions that form the basis of our epsilon-free grammar −

S → a, aA | bB 
A → aA | aS 
B → cS 

Step 3: Replacing Epsilon Productions

Now, we systematically replace all occurrences of non-terminals with epsilon productions in the right-hand sides of our productions.

• In 'A → aA | aS', replacing 'S' with 'ε' yields 'A → aA | ε'. Since 'ε' is the empty string, we can simplify this to 'A → aA'.
• In 'B → cS', replacing 'S' with 'ε' yields 'B → c'.
• In 'S → aA | bB', replacing 'B' with 'ε' yields 'S → aA | b'.

The final productions will be like,

S → a, aA | b 
A → aA | aS | a 
B → cS | c 

Step 4: Handling the Start Symbol

The start symbol 'S' has an epsilon production. This means that the start symbol can derive the empty string, which is often acceptable in finite automata.

However, if the start symbol has an epsilon production, we need to add a new start symbol ('S1' in our example) that inherits all the productions of the original start symbol, including the epsilon production. This new start symbol ensures that the empty string can be accepted by the automata.

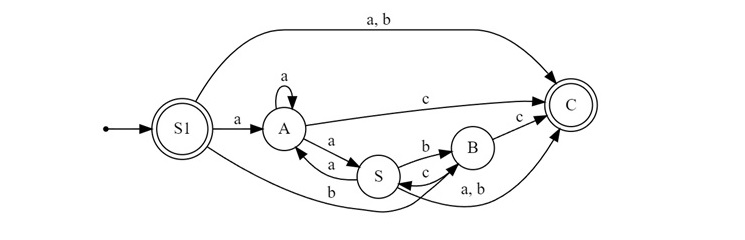
S1 → a | aA | b | bB | ε 
S → a, aA | b 
A → aA | aS | a 
B → cS | c 

Converting the Epsilon-Free Grammar to a Finite Automata

Now it is time to convert the final finite automata from the above grammar. We have five states {S1, S, A, B, C}. The S1 and C will be the final state, S1 is final because it has null transition.

Conclusion

In this chapter, we have had a detailed explanation on how to convert regular grammar to finite automata.

Converting a regular grammar with epsilon productions into a finite automata is a two-step process. First, we eliminate epsilon productions, ensuring a grammar that accurately reflects the desired language without ambiguity introduced by empty transitions. Then, we translate this epsilon-free grammar into a finite automata, capturing the language's structure in a format compatible with finite state machines.