Turing Machine and Grammars in Automata Theory

Previous
Quiz
Next

In this chapter, we will cover the grammars associated with Turing Machines. These concepts are fundamental to understand how the languages can be generated and recognized. Here, we will look into the relationship between Turing machines and unrestricted grammar, and explore how these two concepts connect each other and how a Turing machine can be transformed into an unrestricted grammar.

Turing Machine

For a very brief overview, a Turing machine is a mathematical model of computation that defines an abstract machine. This machine manipulates symbols on a strip of tape according to a set of rules.

A Turing machine can be visualized as having a tape divided into cells, where each cell contains a symbol from a finite alphabet. A read / write head moves left or right across the tape, reading symbols and making decisions based on a finite set of states and transition functions. The Turing machine continues this process until it reaches a halting state, either accepting or rejecting the input string.

Turing Decidability

A problem is said to be Turing decidable if there exists a Turing machine that halts and provides a "yes" or "no" answer for every possible input. The recursive languages that can be decided by Turing machines always lead to a halt, while recursively enumerable languages may not halt, looping infinitely.

Unrestricted Grammar

Unrestricted grammar is a type of formal grammar that is defined without any restrictions on the form of its production rules.

Formally, a grammar G = (VN, Σ, P, S) is called an unrestricted grammar if all its productions are in the form LS → RS, where LS is a string of non-terminal and terminal symbols, and RS is a string of non-terminal and terminal symbols or the empty string. This form of grammar is known as Type 0 grammar in the Chomsky hierarchy, and it is the most general form of grammar.

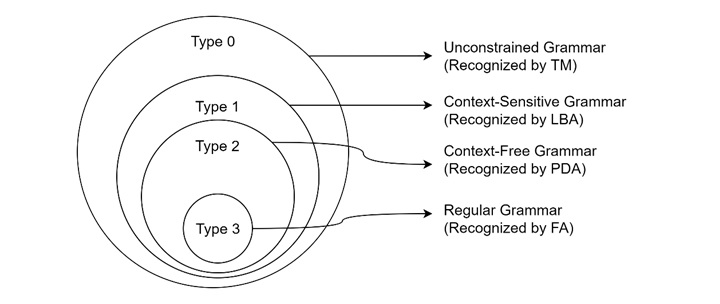
Unrestricted Grammar

The lack of restrictions allows for a more flexible and powerful method of string generation, which leads to the capabilities of a Turing machine.

Every language that can be generated by an unrestricted grammar can be recognized by a Turing machine, and vice versa. This states the idea that the set of languages generated by unrestricted grammar is equivalent to the set of recursively enumerable languages.

Turing Machine and Unrestricted Grammar

The connection between Turing machines and unrestricted grammar can be understood by observing how the rules of a Turing machine can be mapped to the production rules of an unrestricted grammar.

Constructing Type 0 Grammar from a Turing Machine

To convert a Turing machine into an equivalent unrestricted grammar, we follow a systematic process that involves translating the transition functions of the Turing machine into production rules of the grammar.

No Change in Length

  • Right Move − If the Turing machine has a transition δ(qi, aj) → (qk, al, R), where the machine moves right after reading aj in state qi , the corresponding production rule in the grammar is qiaj → al qk.
  • Left Move − If the Turing machine has a transition δ(qi,aj) → (qk, al, L), where the machine moves left, the corresponding production rule in the grammar is ap qi aj → qk ap al, for all allowable tape symbols ap.

Change in Length:

  • Left Bracket ‘[‘ at the Left End − If the Turing machine moves left beyond the leftmost boundary, we introduce a production rule like [ qi aj → qk B al to handle this boundary condition.
  • Right Bracket ‘]’ at the Right End − When the Turing machine moves right beyond the rightmost boundary, a production rule like qi ] → qi B ] is added.

Handling End Markers

To manage the string boundaries, we introduce end markers ψ and $ and corresponding production rules such as [ qi ψ → [ qi and ap for each symbol ap .

Example 1: 1's Complement Conversion

Let us see the idea through some examples for a better understanding. Consider a Turing machine designed to compute the 1's complement of a binary number. The machine's transition functions can be converted into a Type 0 grammar as follows −

Transitions −

$$\mathrm{\delta(Q_{0},\: 0)\: \rightarrow \:(Q_{0},\: 1,\: R)\: becomes \:Q_{0}0\: \rightarrow \:1Q_{0}}$$

$$\mathrm{\delta(Q_{0},\: 1)\: \rightarrow \:(Q_{0},\: 0,\: R)\: becomes \:Q_{0}1\: \rightarrow \:0Q_{0}}$$

$$\mathrm{\delta(Q_{0},\: B)\: \rightarrow \:(Q_{f},\: B,\: R)\: becomes \:Q_{0}B\: \rightarrow \:0Q_{f}}$$

End Markers −

  • [ Qf B] → S, where S is the start symbol of the grammar.

These rules collectively define the unrestricted grammar that is equivalent to the given Turing machine.

Example 2: Even String of 'a'

Let us see another example. Consider a Turing machine that accepts strings containing an even number of 'a's. The equivalent Type 0 grammar can be constructed as follows −

Transitions −

$$\mathrm{\delta(Q_{0},\: a)\: \rightarrow \:(Q_{1},\: B,\: R)\: becomes\: Q_{0}\: a\: \rightarrow \:B\: Q_{1}}$$

$$\mathrm{\delta(Q_{1},\: a)\: \rightarrow \:(Q_{0},\: B,\: R)\: becomes\: Q_{1}\: a\: \rightarrow \:B \:Q_{0}}$$

End Markers −

$$\mathrm{[Q_{0}\: \psi \: \rightarrow \:[ Q_{0}}$$

$$\mathrm{[Q_{1}\: B]\: \rightarrow \: S}$$

This grammar will generate strings that belong to the language of even numbers of 'a's.

Conclusion

Turing Machines use unrestricted grammars. Here we discussed the transformation of a Turing machine into unrestricted grammar, which states the deep connection between computation and language theory.

Unrestricted grammars are the most general form of formal grammars. In this chapter, we presented the examples of two machines with grammars for a clear understanding.

Print Page
Previous
Next
Advertisements