
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Cellular Automata
Cellular Automata are used in various fields such as computer science, mathematics, physics, and biology. It was originally proposed by Stanislaw Ulam and John von Neumann in the 1940s.
Cellular automata provide a simple and also powerful way to simulate complex systems. In this chapter, we will see the basics of cellular automata, discuss their key characteristics, and walk through a detailed example for a better understanding.
Cellular Automata
Cellular Automata consist of a grid of cells, where each cell can be in one of a finite number of states, usually represented as 0 or 1. The grid can be one-dimensional or multi-dimensional.
In this chapter, we will focus on one-dimensional cellular automata first for simplicity. The state of each cell evolves over time according to a set of rules that consider the states of neighbouring cells.
Key Concepts of Cellular Automata
Here are some Key Concepts of Cellular Automata −
- Cells and Grid − The basic unit of a cellular automaton is the cell. Cells are arranged in a grid, which can be one-dimensional (a line), two-dimensional (a plane), or higher dimensions. Each cell has a state, which is updated based on the states of its neighbouring cells.
- Neighbourhood − The neighbourhood of a cell consists of the cell itself and its adjacent cells. In a one-dimensional cellular automaton, a cell typically has two neighbours: one on the left and one on the right. The neighbourhood can also include more distant cells depending on the rules.
- Rules − The evolution of the cellular automaton is controlled by a set of rules. These rules finds the next state of a cell based on the current state of the cell and the states of its neighbours. The rules are applied simultaneously to all cells, and gives a synchronous updates across the grid.
- Discrete Time − Cellular automata evolve in discrete time steps. At each time step, the state of every cell is updated according to the rules, and the entire grid transitions to a new configuration.
Characteristics of Cellular Automata
Cellular automata have several important characteristics that make them unique and useful for modelling complex systems −
- Synchronous Computation − All cells in the grid update their states simultaneously at each time step. This ensures that the evolution of the automaton is uniform and predictable.
- Finite States − Each cell can exist in a finite number of states, usually two (0 or 1), but more states are possible depending on the application.
- Local Interactions − The state of each cell depends only on its own state and the states of its immediate neighbours. This local interaction can lead to complex global behaviour in the automaton.
- Deterministic or Non-Deterministic − Cellular automata can be either deterministic, where the rules produce a single predictable outcome, or non-deterministic, where the rules may allow multiple possible outcomes.
Example of One-Dimensional Cellular Automata
Let us see with a basic example to understand how a one-dimensional cellular automaton works. We will use a simple rule-based system where each cell can be in one of two states: 0 or 1.
The Update Rule
In a one-dimensional cellular automaton, each cell has three neighbours: the cell itself, the cell to its left, and the cell to its right. The next state of a cell is determined by applying a rule to the current states of these three cells.
There are 256 possible rules for a one-dimensional CA with binary states (0 and 1). Each rule can be represented by a binary number, where each bit in the number specifies the next state of the cell for a particular neighbourhood configuration.

In null stuffing 0 is stuffed at both sides of the original sequence. This is described in the following table.
| Original | 1 0 1 0 1 |
| Null Stuffed | 0 1 0 1 0 1 0 |
For example, consider the rule 210. The binary equivalent of 210 is 11010010. This binary number corresponds to the next states for each possible neighbourhood configuration, as shown below −
| Neighbourhood | Next State |
|---|---|
| 111 | 1 |
| 110 | 1 |
| 101 | 0 |
| 100 | 1 |
| 011 | 0 |
| 010 | 0 |
| 001 | 1 |
| 000 | 0 |
The cell representation of 111 and 010 is like the following −

Applying the Rule
Let us apply this rule to an initial configuration of cells. Suppose we start with the following sequence −
Initial Sequence (t0): 1001
Now, we will calculate the next three-time steps (t1, t2, t3) using the wrap-around technique. In this technique, the sequence is considered circular, meaning that the first and last cells are treated as neighbours.
- Time Step 1 (t1) − Neighbourhoods: 110, 100, 001, 011. Next State: 1, 1, 1, 0, Result: 1110
- Time Step 2 (t2) − Neighbourhoods: 011, 110, 101, 011, Next State: 0, 1, 1, 0, Result: 0110
- Time Step 3 (t3) − Neighbourhoods: 001, 010, 100, 000, Next State: 1, 0, 1, 1, Result: 1011
Thus, the evolution of the cellular automaton over three timesteps from the initial sequence 1001 is −
- t0: 1001
- t1: 1110
- t2: 0110
- t3: 1011
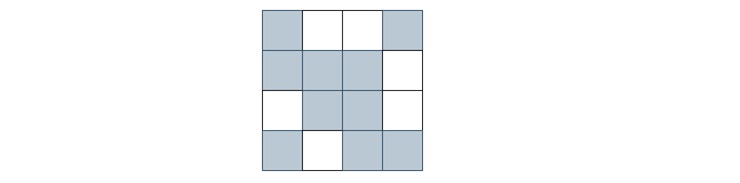
After null stuffing, it will be −
- t0: 010010
- t1: 001100
- t2: 010110
- t3: 000010
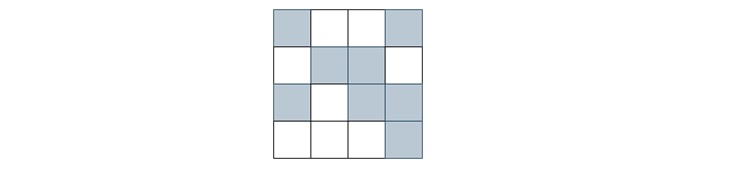
This example shows how a simple set of rules can produce a sequence of states over time in a cellular automaton.
Applications of Cellular Automata
Let us see some of the Cellular automata applications in various fields −
Computer Science
- Cryptography − Cellular automata are used to design secure cryptographic systems by exploiting their complex and unpredictable behaviour.
- Fault Tolerance − In digital circuits, cellular automata can help detect and correct errors by simulating the behaviour of faulty components.
Physics
- Simulation of Gas Behaviour − Cellular automata can model the behaviour of gases, allowing researchers to study properties like diffusion and pressure.
- Forest Fire Propagation − By simulating the spread of fire through a forest, cellular automata can help predict and manage wildfire outbreaks.
Biology
- Bone Erosion Simulation − Cellular automata can simulate biological processes like bone erosion, helping in medical research and treatment planning.
Conclusion
In this chapter, we covered the basic structure of cellular automata including cells, neighbourhoods, rules, and discrete time steps. We also seen a detailed example of a one-dimensional cellular automaton using rule 210. Finally, we discussed the various applications of cellular automata in fields such as computer science, physics, and biology.