Russells Paradox in Automata Theory

---

---

Russell's Paradox is a famous problem in Set Theory that states a fundamental inconsistency in sets theory in mathematics. This paradox was introduced by the British philosopher and logician Bertrand Russell in 1901. Russell's Paradox challenges the idea that we can define sets in a completely unrestricted way. It shows that certain ways of defining sets lead to contradictions.

In this chapter, we will cover the basics of Russell's Paradox, including its origins, a detailed example for a better understanding.

Understanding Set Builder Notation

To begin with, let us discuss the set builder notation. This notation is commonly used and we are familiar with them. The idea is simple: we define a set by specifying a condition that its elements must satisfy.

A typical set builder notation looks like this:

$$\mathrm{S \:=\: \{x \: \in \: T\: |\: P(x)\: \text{ is satisfied} \}}$$

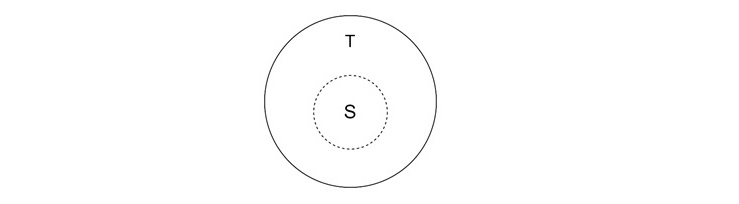
Here, T is a previously known set, and P(x) is a predicate, or a condition that elements of T must satisfy to be included in S. In other words, S is a subset of T containing all the elements from T that satisfy P(x).

Expanding the Concept of Set Builder Notation

A natural question that arises is whether we can expand this concept. Specifically, can we define sets without starting from a previously known set T? Can we define a set directly from the entire mathematical universe? This idea is known as unrestricted comprehension.

For instance, consider the set:

$$\mathrm{S \:=\: \{x \: \in \: T\: |\: P(x)\: \text{ is satisfied} \}}$$

Here, S includes all elements x from the entire mathematical universe that satisfy the predicate P(x). At first glance, this might seem like a reasonable way to define sets. However, this approach leads to significant problems, as we will see with Russell's Paradox.

Introducing Russells Paradox

Russell's Paradox shows that unrestricted comprehension can lead to a contradiction. The paradox is straightforward but deeply troubling.

It begins by considering a set S defined as follows:

$$\mathrm{S \:=\: {x \:|\: x\: \notin \:x}}$$

In simple terms, S is the set of all sets that are not members of themselves. At first, this definition might seem innocent, but it leads to a contradiction. There are two possibilities to consider:

Possibility 1: S is an element of S

If S is an element of itself, then by the definition of S, it must satisfy the condition x ∉ x. But if S satisfies this condition, then S cannot be an element of itself. This leads to a contradiction because we started by assuming that S is an element of itself.

Possibility 2: S is not an element of S

If S is not an element of itself, then it must satisfy the condition for membership in S, which is x ∉ x. But if S satisfies this condition, then S should be an element of itself, leading to another contradiction.

No matter which possibility we choose, it will be a contradiction. It means the set S, as defined, cannot exist. This is the idea of Russells Paradox, the unrestricted comprehension allows us to define a set that leads to a logical contradiction.

Dealing with the Paradox

Russells Paradox creates a significant problem for set theory and mathematics as a whole. If unrestricted comprehension is allowed, it will be contradiction, which can undermine the entire structure of mathematics. To avoid these contradictions, mathematicians concluded that unrestricted comprehension must be disallowed.

Restricting Comprehension

If we have unrestricted comprehension, there must be restricted comprehension as well. The solution to the problem of unrestricted comprehension is to restrict the comprehension.

Instead of allowing sets to be defined from the entire mathematical universe, we restrict the process to subsets of known sets. It means that we can only define a set S by specifying a condition P(x) that applies to elements of a previously known set T:

$$\mathrm{S \:=\: {x \:\in\: T \:|\: P(x)\: \text{ is satisfied}}}$$

This restriction prevents the paradox from arising because it does not allow the formation of problematic sets like the one in Russells Paradox.

The Issue with the Mathematical Universe

However, even with this restriction, there is still an issue to consider. A famous question in set theory is whether the entire mathematical universe V can be considered a set. If we assume that V is a set, then we can apply restricted comprehension to it. But this leads to a problem similar to Russells Paradox.

Suppose V is a set. According to restricted comprehension, we can define a set T as follows:

$$\mathrm{T = \{x \:\in\: V \:|\: x \:\notin\: x \}}$$

This is essentially the same as Russell's Paradox, and it leads to the same contradiction. If T is an element of T, then T must satisfy x ∉ x, so T cannot be an element of itself. But if T is not an element of T, then T satisfies the condition and must be an element of itself. Again, we get a contradiction.

Consider the mathematical universe is not a Set

This reasoning leads to an important conclusion: the mathematical universe cannot be a set. Even though V consists of all possible sets, it is not itself a set. This is a critical insight in set theory and helps prevent the contradictions that arise from unrestricted comprehension.

Conclusion

In this chapter, we explained the Russells Paradox in detail. We started by understanding the set builder notation and then expanded on the idea by considering unrestricted comprehension.

In Russells Paradox, where we defined a set S that included all sets that are not members of themselves. We saw that this definition led to a contradiction, proving that such a set cannot exist. To resolve this issue, we discussed the need to restrict comprehension to subsets of known sets and concluded that the mathematical universe cannot be considered a set itself.