
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Graph and Tree in Automata Theory
In computer science, graph theory is one of the most important concepts in every aspect. In automata theory, we represent the state transition diagrams through directed graphs.
In this chapter, we will explore the basics of graphs and trees with examples, different terminologies and applications in detail.
Concept of Graphs
A graph is an abstract representation of a set of objects connected by directed or undirected links. There are two major components of a Graph:
- Vertices − The interconnected objects in a graph.
- Edges − The links that connect some pairs of vertices.
To represent graphs, we can use sets. A graph G is a set of vertices V and edges E, with end vertices associated with each edge.
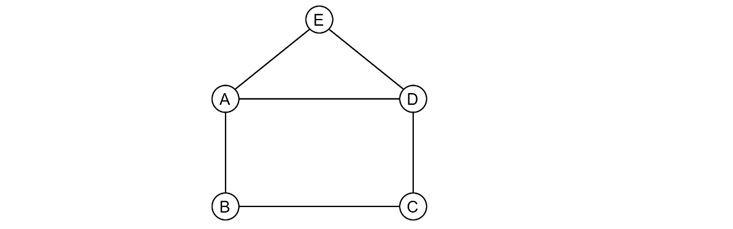
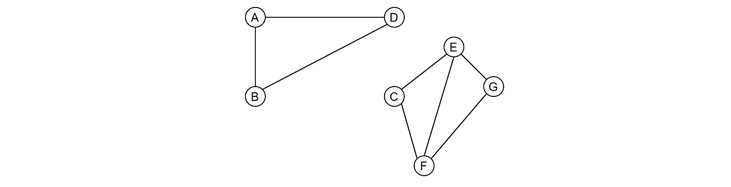
For instance, the graph in the above figure has 5 vertices (A, B, C, D, and E) and 6 edges (AB, BC, CD, DA, DE, and EA). Now let us see several terminologies of graphs
Graph Terminologies
The following terminologies are frequently used Graph Theory −
- Incident Edges − The edges that meet at a common vertex are known as incident on that vertex which is common.
- Degree of a Vertex − The number of edges incident on a specific vertex is known as degree of the vertex. If the edge is a self-loop, it will be counted twice.
- Isolated Vertex − A vertex of a graph having no incident edge is known as isolated vertex.
- Pendant Vertex − When a vertex of degree one is there in a graph. That is known as pendant vertex or end vertex.
From the above example, it is clear that the graph has edges AE, AB, and AD, with vertex A having a degree of 3. It can be proven that the number of odd degree vertices in a graph is always even.
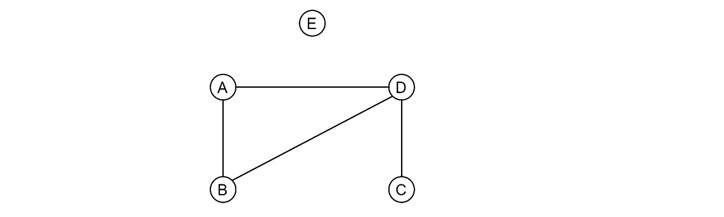
And in this example, the vertex E has no incident edges so this is isolated vertex, where the C has only one incident edge, this is pendent or end vertex.
Graph Traversal
In a graph, we need to traverse through the graph to get the nodes and their values. Based on the idea there are several terminologies associated to graph traversal. Let us understand one by one.
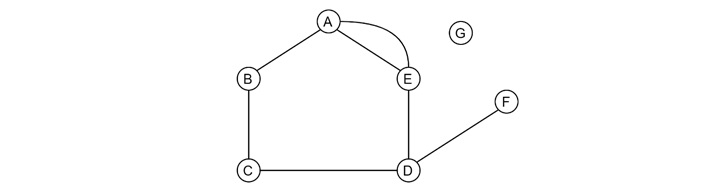
What is a Walk in Graph Theory?
A walk is a sequence of vertices and edges starting from a vertex, traversing edges, and ending at a vertex. It is a finite alternating sequence, starting and ending with vertices. A walk must not have multiple edges or a vertex traversed.
For example − For the graph above, B(BC)C(CD)D(DF)F is a walk. The label in () represents edge.
There are two types of walks −
- Closed Walk − If we end the walk at the initial starting vertex then that is closed walk.
- Open Walk − If we end the walk at any vertex other than the initial starting vertex then that is open walk.
Circuit in Graph Theory
A circuit is nothing but a walk, more specifically a closed walk, where no vertex appears more than once.
Paths in Graph Theory
A path is a type of open walk, where no vertex appears more than once.
Types of Graphs
We can also classify the graphs into two types −
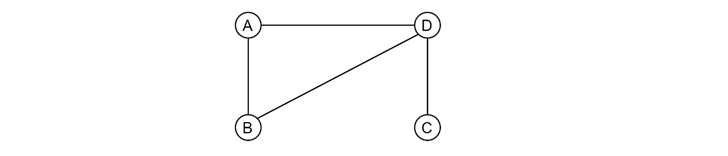
Connected Graph
Where a graph is a single connected component, then it is regarded as a connected graph.
Disconnected Graph
When multiple disconnected components are present, then it is known as a disconnected graph
Role of Trees in Automata
A tree is an undirected connected graph with no circuit. Trees are a special type of graph with unique properties and applications. Trees (rooted-trees) contains specially designed vertex called a root.
The rest of the nodes in a tree can be partitioned into t disjoint sets (t ≥ 0), where each set represents a tree . These are called sub-trees.
For example, a sample tree is given in the following figure −
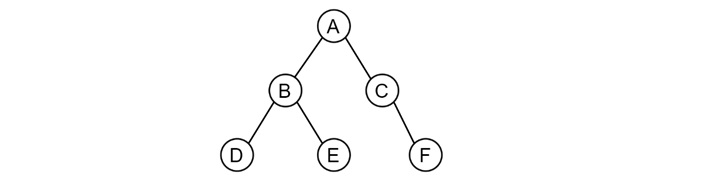
Tree Terminologies
In the following table, some tree terminologies are given −
| Term | Definition |
|---|---|
| Root | The topmost node of the tree. |
| Sub-trees | Disjoint sets of nodes that form individual trees within the main tree. |
| Degree of a Node | The number of sub-trees of a node. |
| Leaf Node (Terminal Node) | A vertex of a tree having degree 0. |
| Non-terminal Nodes | Nodes other than the leaf nodes. |
| Parent Node | In a rooted tree, the vertex connected to a given vertex on the path to the root. |
| Child Node | A vertex that has a parent node. |
| Siblings | The children of the same parent node. |
| Depth of a Node | The length of the path from the root of the tree to the node. |
| Level of a Tree | The set of all nodes at a given depth. |
| Height of a Tree | The length of the path from the root to the deepest node in the tree. |
Tree Properties
Let us see some of the important properties of Trees −
- Number of Nodes in a Full Binary Tree − For a full binary tree, the number of nodes is given by the formula: , where h is the height of the tree.
- Number of Nodes in a Complete Binary Tree − For a complete binary tree, the number of nodes will be in range, , where h is the height of the tree.
Applications of Graphs and Trees
The following table highlights the applications of Graphs and Trees in Automata –
| Structure | Application | Description |
|---|---|---|
| Graphs and Trees | Data Structures | Fundamental structures used to organize and represent various types of information in computer science. |
| Graphs and Trees | Algorithms | Many algorithms, particularly those involving search and traversal, are based on graph and tree structures. |
| Graphs | Network Modeling | Can be used to model and analyze networks, which could include computer networks, social networks, or other interconnected systems. |
| Trees | File Systems | Tree structures are often used to represent hierarchical file systems in computers. |
Conclusion
In this chapter, we explained the concept of graphs and their special types called trees. We also highlighted their types, properties, important terminologies with formula and diagrams. We also discussed the applications of graphs and trees.