Regular Expression to ∈-NFA

---

---

Among the different types of automata, the ∈ - NFA (Epsilon Non-deterministic Finite Automaton) is a special kind that extends the concept of a regular NFA. In this chapter, we will see the basic concept of ∈ - NFA and provide a step-by-step example of converting a regular expression to an ∈ - NFA for a better understanding.

What is ∈ - NFA?

Let us discuss the idea of ∈ - NFA before getting into the conversion process.

An ∈ - NFA is similar to an NFA but with a key difference: it allows transitions on the empty string (denoted by ∈). This means that the automaton can change its state without consuming any input symbols.

Formally, an ∈ - NFA is represented as a 5-tuple −

• Q − The set of all states.
• q0 − The initial state.
• Σ − The set of input symbols.
• δ − The transition function, defined as $\mathrm{\delta \: :\: Q \:\times\: (\Sigma\: \cup\: \{\in\}) \:\rightarrow \:2^Q}$.
• F − The set of final states.

The transition function in ∈ - NFA is what sets it apart from a regular NFA. In a regular NFA, transitions occur based on input symbols, while in an ∈ - NFA, transitions can also occur without any input (via ∈ - transitions).

Rules for Constructing ∈ - NFA

To construct an ∈ - NFA from a regular expression, there are specific rules to follow. Let us go through these rules one by one.

∈ - NFA for a⁺

The expression a⁺ indicates that the automaton must accept one or more occurrences of the symbol 'a'. The ∈ - NFA for a+ can be constructed as follows −

In this diagram,

• q0 is the initial state.
• q1 is an intermediate state which is reachable from q0 with null move.
• q2 is the state, where the first a is accepted. And for more a, it will come to q1 with null move.
• q3 is the final state, here from q2 it can reach with null move.

∈ - NFA for a*

The expression a* signifies that the automaton can accept zero or more occurrences of a. The ∈-NFA for a* is slightly modified from a+ by adding a loop that allows the automaton to remain in the initial state even if no a is encountered −

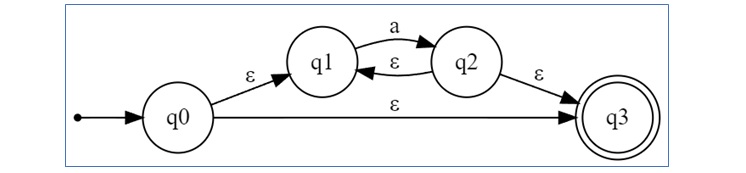
Here, the automaton can transition from q0 to q3 directly without consuming any input, representing the acceptance of an empty string.

∈-NFA for a + b

The expression a + b operates like an OR logic, meaning that the automaton can accept either a or b. The ∈-NFA for a + b is constructed with two parallel paths −

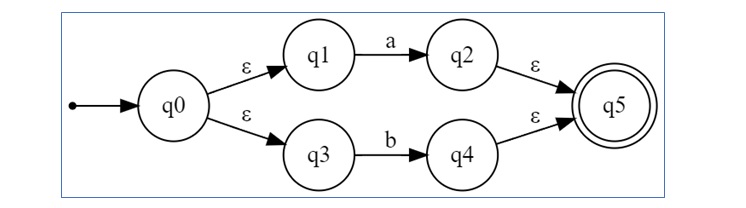
In this structure q0 transitions to q1 on null, then a to q2 and again null to q5. Similarly, q0 to q3 with null and q3 to q4 with b and q4 to q5 with null.

∈-NFA for ab

The concatenation of a followed by b is expressed as ab. The automaton must accept a and then b in sequence −

OR

This rule ensures that the automaton moves through the states sequentially, accepting a and then b before reaching the final state.

Example of Constructing ∈-NFA for L = bc(ab+c)*a⁺

Now that we have understood the basic rules for constructing an ∈-NFA, let's apply them to the regular expression L = bc(ab + c)*a⁺.

Breakdown of Regular Expression

The regular expression can be divided into three parts −

• bc − A concatenation of b followed by c.
• (ab+c)* − A combination of concatenation and OR logic repeated zero or more times.
• a⁺ − One or more occurrences of a.

Constructing ∈-NFA for (ab + c)*

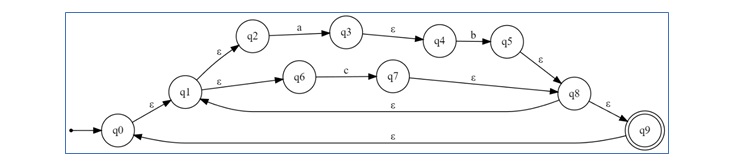
Constructing final ∈-NFA

Conclusion

In this chapter, we covered the concept of ∈-NFA and understood how to construct an ∈-NFA from a regular expression. We broke down the regular expression L = bc(ab+c)*a⁺ into its components and applied the rules for constructing ∈-NFA. The final automaton represents a system that can accept the given regular language, demonstrating the power and flexibility of ∈-NFA in handling complex regular expressions.