
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Turing Machine for Subtraction in Automata Theory
Read this chapter to learn how a Turing Machine can be used to perform subtraction of two integers. Although Turing Machines for subtraction can be little bit complex, but they can efficiently solve the subtraction.
Here, we will break down the process into easy-to-understand steps and provide examples to illustrate how subtraction is done using a Turing Machine, for a better understanding.
Basic Structure of a Turing Machine for Subtraction
To perform subtraction using a Turing Machine, we represent the numbers on the tape using a series of symbols, typically zeros (0), with a separator between the numbers. For example, if we want to subtract two numbers, x and y, we can represent them on the tape as −
$$\mathrm{0^{x}\: 10^{y}}$$
Here, 0x represents the first number x, 1 is the separator, and 0y represents the second number y.
The subtraction operation, f(x, y) = x - y, will be performed by the Turing Machine in a series of steps, modifying the tape according to the rules defined in the transition function.
Step-by-Step Subtraction Process
The Turing Machine performs subtraction by following these steps −
- Initial Setup − The machine starts at the leftmost end of the tape and moves right, replacing the first 0 of x with a blank B. This indicates that the first number is being processed.
- Traverse the First Number − The machine continues to traverse the tape, moving right through the rest of the zeros in the first number until it reaches the separator 1.
- Processing the Separator − When the machine encounters the 1, it changes state and moves to process the second number y.
- Subtraction Process − The machine starts subtracting by replacing the leftmost 0 of y with 1. This action represents subtracting one unit from x.
- Return to the Start − The machine then moves left, back to the beginning of the first number, to repeat the process until either all of y is subtracted from x, or it detects that y is greater than x.
- Final Steps − If y is subtracted completely and x > y, the remaining zeros represent the result x - y. If y is greater than x, the machine will clear the tape, resulting in 0, indicating that the result is zero.
The transition diagram for this process is shown below −
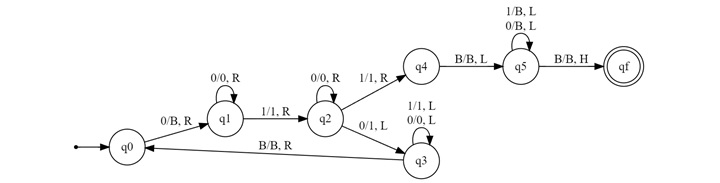
Example 1: Subtracting Two Numbers
Lets work through an example to subtract 5 3 using the Turing Machine. Here is how we would represent this operation on the tape −
Copy code 000001000
This setup represents the numbers 5 and 3 to be subtracted.
The steps are as follows −
- Initial State (q0) − The machine starts in state q0, reading the first 0. It changes the first 0 of x to B, indicating that the number is being processed, and moves to the right, transitioning to state q1.
- Traverse First Number − The machine continues to move right through the remaining zeros of x, staying in state q1 until it encounters 1.
- Processing Separator (q2) − Upon encountering the separator 1, the machine moves right into state q2 and starts processing the second number y.
- Subtracting (q3) − The machine replaces the leftmost 0 of y with 1, indicating that one unit has been subtracted from x, and moves left to start the process over.
- Repeat Process − The machine repeats the process until all 0s in y have been processed, leaving the tape as 00, which represents 2, the result of 5 - 3.
- Final State − The machine halts in state q6 when the subtraction is complete, and the final tape configuration is 00, representing the result 2.
Example 2
Construct a Turing machine (TM) for subtraction of two unary integers.
Solution
Subtraction of two unary integers
$$\mathrm{3 \:-\: 2 \:=\: 1}$$
In Turing Machine 3 represents: 111 and 2 represents: 11
Let "M" be a symbol used to separate two integers
| B | 1 | 1 | 1 | M | 1 | 1 | B |
Here B = blank
M = Symbol used two separate two integers

Algorithm
Follow the step wise algorithm given below to construct a TM for subtraction −
Step 1 − Let's take two unary integers as an input. We start from the initial state q0.
Step 2 − If we find the 1 in the string then go to the same state without changing the value of 1, and go to the right of the string.
Step 3 − If we find the m symbol then ignore this symbol without changing the symbol and go to the right of the string.
Step 4 − If we find the 1 after the pass the M symbol then change the value of 1 into the X and go to the left of the string.
Step 5 − Then pass the symbol of M and go to the left and if we find the 1 then change the value of 1 to X and go to the right.
Step 6 − So, this type after the symbol(M) we change all values of 1's into X and the same total number of 1's change into the X before the symbol M.
Step 7 − Apply these steps and get the Turing machine subtraction of two unary integers.
While working with subtraction, the Turing machine considers any of the three cases based on input given by the user.
If "a" and "b" are two integers, we have two consider whether −
$$\mathrm{a \: \gt \: b}$$
$$\mathrm{a \: \lt \: b}$$
$$\mathrm{a \: = \: b}$$
By consider all the three conditions, the final Turing machine is as follows −

Explanation of the Diagram
Step 1 − Consider an input string as 110111
i.e. a = 11 and b = 111, according to given input a
Step 2 − Scan string from left to right.
Step 3 − Mark '1' as 'X' and then move to the right.
Step 4 − Reaching to the right of '0' and marking '1' as 'X' and moving left.
Step 5 − Reaching 'X' on left of '0' and moving one step right.
Step 6 − Again mark '1' as 'X' and then move to the right.
Step 7 − Reaching to the right of '0' and passing 'X', mark '1' as 'X' and move left.
Step 8 − Reach 'X' in the left of '0'and move one step right.
Step 9 − If there is a "0" after 'X' that means all '1's are finished before '0'.
Step 10 − Pass '0', 'X' and there is '1' remaining. That is, the second number is greater than the first one.
Step 11 − And then the final state is "a < b"
Turing Machine for the Function f(x) = x - 2
In this section, we will discuss how a Turing Machine can be used to compute the function f(x) = x - 2. This function involves subtracting 2 from a given number x. The process is straightforward but highlights the flexibility of Turing Machines in performing simple arithmetic operations.
Representation of the Input
To represent the integer x on the Turing Machines tape, we use a sequence of zeros (0). The input for the function f(x) = x 2 is written as −
$$\mathrm{0^{x} B}$$
Here, 0x represents the integer xxx, and B is the blank space following the number.
Step-by-Step Process to Compute f(x) = x 2
The Turing Machine computes result using the following these steps −
- Traverse the Input Number − The machine starts at the leftmost end of the tape and moves right, traversing the sequence of zeros (0x) that represent the number x.
- Subtract the First Zero − When the machine reaches the end of the sequence of zeros, just before the blank B, it changes the state and replaces the last 0 with B, effectively subtracting one zero from x.
- Subtract the Second Zero − The machine moves left to find the next 0 and replaces this 0 with another B, thereby subtracting the second zero.
- Handle Small Values of xxx − If x is less than or equal to 2, the machine will encounter a situation where it cannot subtract two zeros. In such cases, the machine will clear the tape, leaving only a blank to indicate that the result is zero.
- Halt − The machine halts after subtracting two zeros. The final state of the tape represents x 2.
Shown below is the transition diagram that illustrates these steps −

Conclusion
In this chapter, we explained in detail how you can perform the subtraction operation using a Turing Machine. We presented the basic concept along with the state transition diagrams for a better understanding.