
- Design and Analysis of Algorithms
- Home
- Basics of Algorithms
- DAA - Introduction to Algorithms
- DAA - Analysis of Algorithms
- DAA - Methodology of Analysis
- DAA - Asymptotic Notations & Apriori Analysis
- DAA - Time Complexity
- DAA - Master's Theorem
- DAA - Space Complexities
- Divide & Conquer
- DAA - Divide & Conquer Algorithm
- DAA - Max-Min Problem
- DAA - Merge Sort Algorithm
- DAA - Strassen's Matrix Multiplication
- DAA - Karatsuba Algorithm
- DAA - Towers of Hanoi
- Greedy Algorithms
- DAA - Greedy Algorithms
- DAA - Travelling Salesman Problem
- DAA - Prim's Minimal Spanning Tree
- DAA - Kruskal's Minimal Spanning Tree
- DAA - Dijkstra's Shortest Path Algorithm
- DAA - Map Colouring Algorithm
- DAA - Fractional Knapsack
- DAA - Job Sequencing with Deadline
- DAA - Optimal Merge Pattern
- Dynamic Programming
- DAA - Dynamic Programming
- DAA - Matrix Chain Multiplication
- DAA - Floyd Warshall Algorithm
- DAA - 0-1 Knapsack Problem
- DAA - Longest Common Subsequence Algorithm
- DAA - Travelling Salesman Problem using Dynamic Programming
- Randomized Algorithms
- DAA - Randomized Algorithms
- DAA - Randomized Quick Sort Algorithm
- DAA - Karger's Minimum Cut Algorithm
- DAA - Fisher-Yates Shuffle Algorithm
- Approximation Algorithms
- DAA - Approximation Algorithms
- DAA - Vertex Cover Problem
- DAA - Set Cover Problem
- DAA - Travelling Salesperson Approximation Algorithm
- Sorting Techniques
- DAA - Bubble Sort Algorithm
- DAA - Insertion Sort Algorithm
- DAA - Selection Sort Algorithm
- DAA - Shell Sort Algorithm
- DAA - Heap Sort Algorithm
- DAA - Bucket Sort Algorithm
- DAA - Counting Sort Algorithm
- DAA - Radix Sort Algorithm
- DAA - Quick Sort Algorithm
- Searching Techniques
- DAA - Searching Techniques Introduction
- DAA - Linear Search
- DAA - Binary Search
- DAA - Interpolation Search
- DAA - Jump Search
- DAA - Exponential Search
- DAA - Fibonacci Search
- DAA - Sublist Search
- DAA - Hash Table
- Graph Theory
- DAA - Shortest Paths
- DAA - Multistage Graph
- DAA - Optimal Cost Binary Search Trees
- Heap Algorithms
- DAA - Binary Heap
- DAA - Insert Method
- DAA - Heapify Method
- DAA - Extract Method
- Complexity Theory
- DAA - Deterministic vs. Nondeterministic Computations
- DAA - Max Cliques
- DAA - Vertex Cover
- DAA - P and NP Class
- DAA - Cook's Theorem
- DAA - NP Hard & NP-Complete Classes
- DAA - Hill Climbing Algorithm
- DAA Useful Resources
- DAA - Quick Guide
- DAA - Useful Resources
- DAA - Discussion
Towers of Hanoi
Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs/rods) and more than one rings is as depicted −
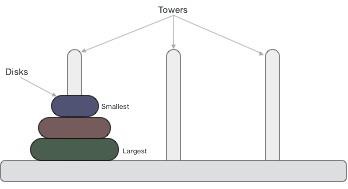
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
Rules in Towers of Hanoi
The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −
Only one disk can be moved among the towers at any given time.
Only the "top" disk can be removed.
No large disk can sit over a small disk.
Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.
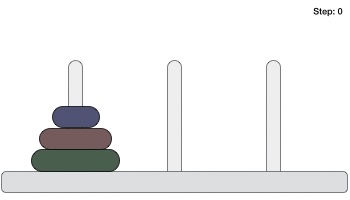
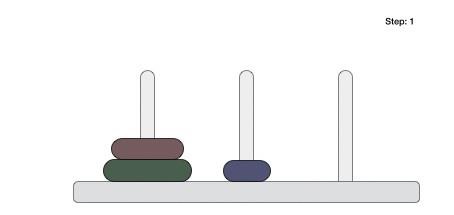
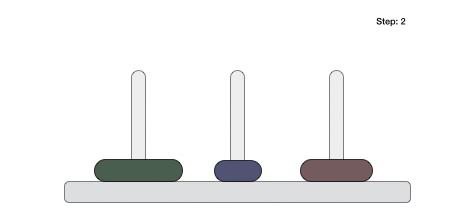
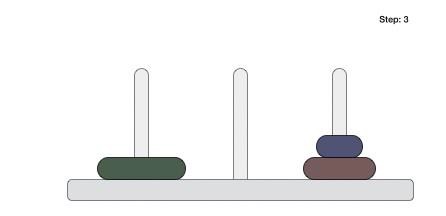
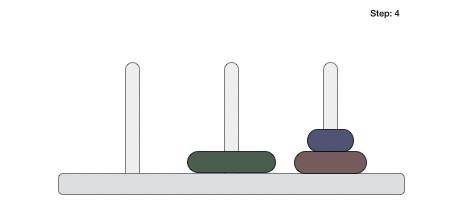
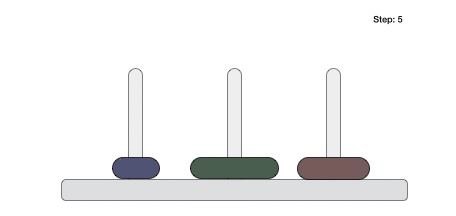
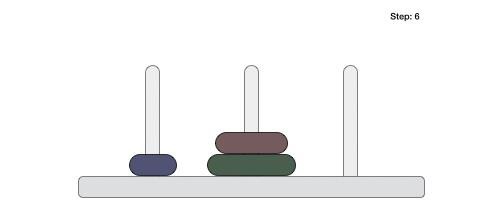
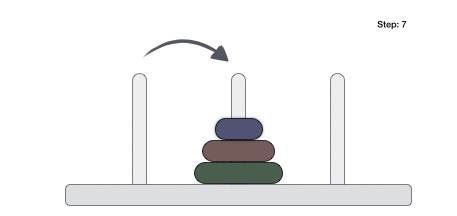
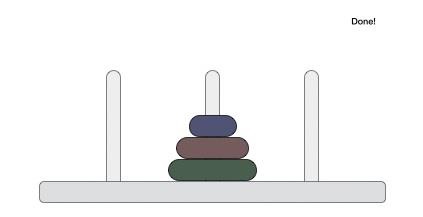
Tower of Hanoi puzzle with n disks can be solved in minimum 2n−1 steps. This presentation shows that a puzzle with 3 disks has taken 23−1 = 7 steps.
Towers of Hanoi Algorithm
To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg.
If we have 2 disks −
First, we move the smaller (top) disk to aux peg.
Then, we move the larger (bottom) disk to destination peg.
And finally, we move the smaller disk from aux to destination peg.
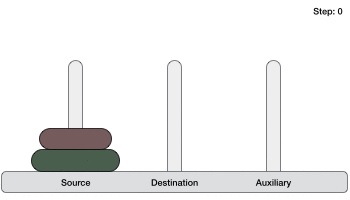
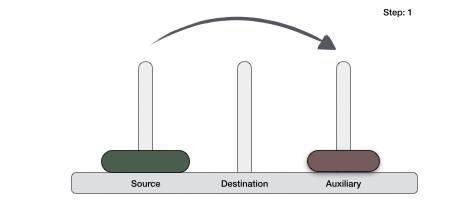
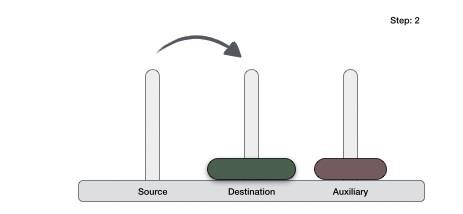
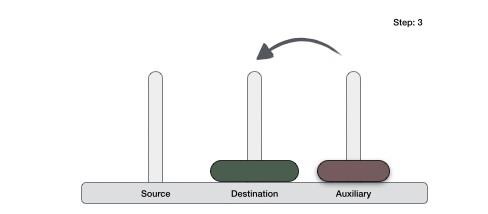
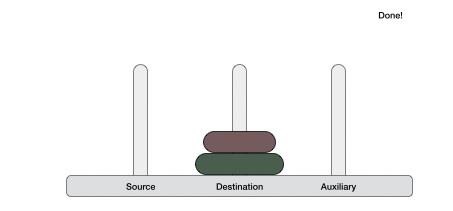
So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part.
Our ultimate aim is to move disk n from source to destination and then put all other (n-1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.
The steps to follow are −
Step 1 − Move n-1 disks from source to aux Step 2 − Move nth disk from source to dest Step 3 − Move n-1 disks from aux to dest
A recursive algorithm for Tower of Hanoi can be driven as follows −
START
Procedure Hanoi(disk, source, dest, aux)
IF disk == 0, THEN
move disk from source to dest
ELSE
Hanoi(disk - 1, source, aux, dest) // Step 1
move disk from source to dest // Step 2
Hanoi(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOP
Example
Following is the iterative approach to implement Towers of Hanoi in various languages.
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <limits.h>
// structure to store data of a stack
struct Stack {
unsigned size;
int top;
int *arr;
};
// function to create a stack of given size.
struct Stack* stack_creation(unsigned size){
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
stack -> size = size;
stack -> top = -1;
stack -> arr = (int*) malloc(stack -> size * sizeof(int));
return stack;
}
// to check if stack is full
int isFull(struct Stack* stack){
return (stack->top == stack->size - 1);
}
// to check if stack is empty
int isEmpty(struct Stack* stack){
return (stack->top == -1);
}
// insertion in stack
void push(struct Stack *stack, int item){
if (isFull(stack))
return;
stack -> arr[++stack -> top] = item;
}
// deletion in stack
int pop(struct Stack* stack){
if (isEmpty(stack))
return INT_MIN;
return stack -> arr[stack -> top--];
}
//printing the movement of disks
void movement(char src, char dest, int disk){
printf("Move the disk %d from \'%c\' to \'%c\'\n",disk, src, dest);
}
//Moving disks between two poles
void DiskMovement(struct Stack *src,
struct Stack *dest, char s, char d){
int pole1Disk1 = pop(src);
int pole2Disk1 = pop(dest);
if (pole1Disk1 == INT_MIN) {
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else if (pole2Disk1 == INT_MIN) {
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
} else if (pole1Disk1 > pole2Disk1) {
push(src, pole1Disk1);
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else {
push(dest, pole2Disk1);
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
}
}
//Towers of Hanoi implementation
void Iterative_TOH(int disk_count, struct Stack *src, struct Stack *aux, struct Stack *dest){
int i, total_moves;
char s = 'S', d = 'D', a = 'A';
if (disk_count % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_moves = pow(2, disk_count) - 1;
for (i = disk_count; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_moves; i++) {
if (i % 3 == 1)
DiskMovement(src, dest, s, d);
else if (i % 3 == 2)
DiskMovement(src, aux, s, a);
else if (i % 3 == 0)
DiskMovement(aux, dest, a, d);
}
}
int main(){
unsigned disk_count = 3;
struct Stack *src, *dest, *aux;
// Three stacks are created with number of buckets equal to number of disks
src = stack_creation(disk_count);
aux = stack_creation(disk_count);
dest = stack_creation(disk_count);
Iterative_TOH(disk_count, src, aux, dest);
return 0;
}
Output
Move the disk 1 from 'S' to 'D' Move the disk 2 from 'S' to 'A' Move the disk 1 from 'D' to 'A' Move the disk 3 from 'S' to 'D' Move the disk 1 from 'A' to 'S' Move the disk 2 from 'A' to 'D' Move the disk 1 from 'S' to 'D'
#include <iostream>
#include <cmath>
#include <climits>
using namespace std;
// structure to store data of a stack
struct Stack {
unsigned size;
int top;
int *arr;
};
// function to create a stack of given size.
struct Stack* stack_creation(unsigned size){
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
stack -> size = size;
stack -> top = -1;
stack -> arr = (int*) malloc(stack -> size * sizeof(int));
return stack;
}
// to check if stack is full
int isFull(struct Stack* stack){
return (stack->top == stack->size - 1);
}
// to check if stack is empty
int isEmpty(struct Stack* stack){
return (stack->top == -1);
}
// insertion in stack
void push(struct Stack *stack, int item){
if (isFull(stack))
return;
stack -> arr[++stack -> top] = item;
}
// deletion in stack
int pop(struct Stack* stack){
if (isEmpty(stack))
return INT_MIN;
return stack -> arr[stack -> top--];
}
//printing the movement of disks
void movement(char src, char dest, int disk){
cout << "Move the disk " << disk << " from " << src << " to " << dest <<endl;
}
//Moving disks between two poles
void DiskMovement(struct Stack *src,
struct Stack *dest, char s, char d){
int pole1Disk1 = pop(src);
int pole2Disk1 = pop(dest);
if (pole1Disk1 == INT_MIN) {
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else if (pole2Disk1 == INT_MIN) {
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
} else if (pole1Disk1 > pole2Disk1) {
push(src, pole1Disk1);
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else {
push(dest, pole2Disk1);
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
}
}
//Towers of Hanoi implementation
void Iterative_TOH(int disk_count, struct Stack *src, struct Stack *aux, struct Stack *dest){
int i, total_moves;
char s = 'S', d = 'D', a = 'A';
if (disk_count % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_moves = pow(2, disk_count) - 1;
for (i = disk_count; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_moves; i++) {
if (i % 3 == 1)
DiskMovement(src, dest, s, d);
else if (i % 3 == 2)
DiskMovement(src, aux, s, a);
else if (i % 3 == 0)
DiskMovement(aux, dest, a, d);
}
}
int main(){
unsigned disk_count = 3;
struct Stack *src, *dest, *aux;
// Three stacks are created with number of buckets equal to number of disks
src = stack_creation(disk_count);
aux = stack_creation(disk_count);
dest = stack_creation(disk_count);
Iterative_TOH(disk_count, src, aux, dest);
return 0;
}
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D
import java.util.*;
import java.lang.*;
import java.io.*;
// Tower of Hanoi
public class Iterative_TOH {
//Stack
class Stack {
int size;
int top;
int arr[];
}
// Creating Stack
Stack stack_creation(int size) {
Stack stack = new Stack();
stack.size = size;
stack.top = -1;
stack.arr = new int[size];
return stack;
}
//to check if stack is full
boolean isFull(Stack stack) {
return (stack.top == stack.size - 1);
}
//to check if stack is empty
boolean isEmpty(Stack stack) {
return (stack.top == -1);
}
//Insertion in Stack
void push(Stack stack, int item) {
if (isFull(stack))
return;
stack.arr[++stack.top] = item;
}
//Deletion from Stack
int pop(Stack stack) {
if (isEmpty(stack))
return Integer.MIN_VALUE;
return stack.arr[stack.top--];
}
// Function to movement disks between the poles
void Diskmovement(Stack src, Stack dest, char s, char d) {
int pole1 = pop(src);
int pole2 = pop(dest);
// When pole 1 is empty
if (pole1 == Integer.MIN_VALUE) {
push(src, pole2);
movement(d, s, pole2);
}
// When pole2 pole is empty
else if (pole2 == Integer.MIN_VALUE) {
push(dest, pole1);
movement(s, d, pole1);
}
// When top disk of pole1 > top disk of pole2
else if (pole1 > pole2) {
push(src, pole1);
push(src, pole2);
movement(d, s, pole2);
}
// When top disk of pole1 < top disk of pole2
else {
push(dest, pole2);
push(dest, pole1);
movement(s, d, pole1);
}
}
//Function to show the movementment of disks
void movement(char source, char destination, int disk) {
System.out.println("Move the disk " + disk + " from " + source + " to " + destination);
}
// Implementation
void Iterative(int num, Stack src, Stack aux, Stack dest) {
int i, total_count;
char s = 'S', d = 'D', a = 'A';
// Rules in algorithm will be followed
if (num % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_count = (int)(Math.pow(2, num) - 1);
// disks with large diameter are pushed first
for (i = num; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_count; i++) {
if (i % 3 == 1)
Diskmovement(src, dest, s, d);
else if (i % 3 == 2)
Diskmovement(src, aux, s, a);
else if (i % 3 == 0)
Diskmovement(aux, dest, a, d);
}
}
// Main Function
public static void main(String[] args) {
// number of disks
int num = 3;
Iterative_TOH ob = new Iterative_TOH();
Stack src, dest, aux;
src = ob.stack_creation(num);
dest = ob.stack_creation(num);
aux = ob.stack_creation(num);
ob.Iterative(num, src, aux, dest);
}
}
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D
#Iterative Towers of Hanoi
INT_MIN = -723489710
class Stack:
def __init__(self, size):
self.size = size
self.top = -1
self.arr = []
# to check if the stack is full
def isFull(self, stack):
return stack.top == stack.size - 1
# to check if the stack is empty
def isEmpty(self, stack):
return stack.top == -1
# Insertion in Stack
def push(self, stack, item):
if self.isFull(stack):
return
stack.top+=1
stack.arr.append(item)
# Deletion from Stack
def pop(self, stack):
if self.isEmpty(stack):
return INT_MIN
stack.top-=1
return stack.arr.pop()
def DiskMovement(self, src, dest, s, d):
pole1 = self.pop(src);
pole2 = self.pop(dest);
# When pole 1 is empty
if(pole1 == INT_MIN):
self.push(src, pole2)
self.Movement(d, s, pole2)
# When pole2 pole is empty
elif (pole2 == INT_MIN):
self.push(dest, pole1)
self.Movement(s, d, pole1)
# When top disk of pole1 > top disk of pole2
elif (pole1 > pole2):
self.push(src, pole1)
self.push(src, pole2)
self.Movement(d, s, pole2)
# When top disk of pole1 < top disk of pole2
else:
self.push(dest, pole2)
self.push(dest, pole1)
self.Movement(s, d, pole1)
# Function to show the Movementment of disks
def Movement(self, source, destination, disk):
print("Move the disk "+str(disk)+" from "+source+" to " + destination)
# Implementation
def Iterative(self, num, src, aux, dest):
s, d, a = 'S', 'D', 'A'
# Rules in algorithm will be followed
if num % 2 == 0:
temp = d
d = a
a = temp
total_count = int(pow(2, num) - 1)
# disks with large diameter are pushed first
i = num
while(i>=1):
self.push(src, i)
i-=1
i = 1
while(i <= total_count):
if (i % 3 == 1):
self.DiskMovement(src, dest, s, d)
elif (i % 3 == 2):
self.DiskMovement(src, aux, s, a)
elif (i % 3 == 0):
self.DiskMovement(aux, dest, a, d)
i+=1
# number of disks
num = 3
# stacks created for src , dest, aux
src = Stack(num)
dest = Stack(num)
aux = Stack(num)
# solution for 3 disks
sol = Stack(0)
sol.Iterative(num, src, aux, dest)
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D

To Continue Learning Please Login