
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Exponential Search Algorithm
Exponential search algorithm targets a range of an input array in which it assumes that the required element must be present in and performs a binary search on that particular small range. This algorithm is also known as doubling search or finger search.
It is similar to jump search in dividing the sorted input into multiple blocks and conducting a smaller scale search. However, the difference occurs while performing computations to divide the blocks and the type of smaller scale search applied (jump search applies linear search and exponential search applies binary search).
Hence, this algorithm jumps exponentially in the powers of 2. In simpler words, the search is performed on the blocks divided using pow(2, k) where k is an integer greater than or equal to 0. Once the element at position pow(2, n) is greater than the key element, binary search is performed on the current block.
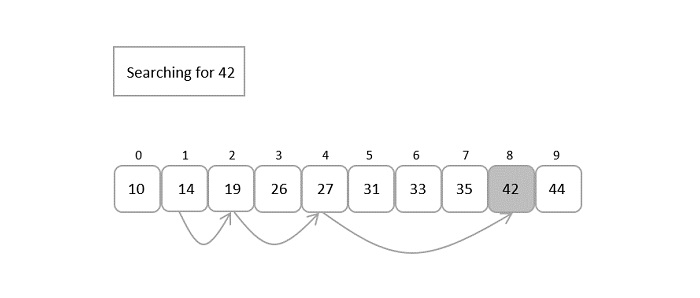
Exponential Search Algorithm
In the exponential search algorithm, the jump starts from the 1st index of the array. So we manually compare the first element as the first step in the algorithm.
Step 1 − Compare the first element in the array with the key, if a match is found return the 0th index.
Step 2 − Initialize i = 1 and compare the ith element of the array with the key to be search. If it matches return the index.
Step 3 − If the element does not match, jump through the array exponentially in the powers of 2. Therefore, now the algorithm compares the element present in the incremental position.
Step 4 − If the match is found, the index is returned. Otherwise Step 2 is repeated iteratively until the element at the incremental position becomes greater than the key to be searched.
Step 5 − Since the next increment has the higher element than the key and the input is sorted, the algorithm applies binary search algorithm on the current block.
Step 6 − The index at which the key is present is returned if the match is found; otherwise it is determined as an unsuccessful search.
Pseudocode
Begin
m := pow(2, k) // m is the block size
start := 1
low := 0
high := size – 1 // size is the size of input
if array[0] == key
return 0
while array[m] <= key AND m < size do
start := start + 1
m := pow(2, start)
while low <= high do:
mid = low + (high - low) / 2
if array[mid] == x
return mid
if array[mid] < x
low = mid + 1
else
high = mid - 1
done
return invalid location
End
Analysis
Even though it is called Exponential search it does not perform searching in exponential time complexity. But as we know, in this search algorithm, the basic search being performed is binary search. Therefore, the time complexity of the exponential search algorithm will be the same as the binary search algorithm’s, O(log n).
Example
To understand the exponential search algorithm better and in a simpler way, let us search for an element in an example input array using the exponential search algorithm −
The sorted input array given to the search algorithm is −

Let us search for the position of element 81 in the given array.
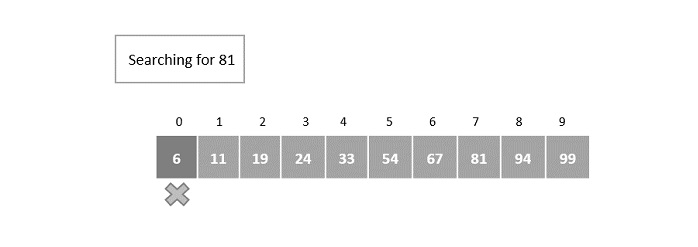
Step 1
Compare the first element of the array with the key element 81.
The first element of the array is 6, but the key element to be searched is 81; hence, the jump starts from the 1st index as there is no match found.
Step 2
After initializing i = 1, the key element is compared with the element in the first index. Here, the element in the 1st index does not match with the key element. So it is again incremented exponentially in the powers of 2.
The index is incremented to 2m = 21 = the element in 2nd index is compared with the key element.
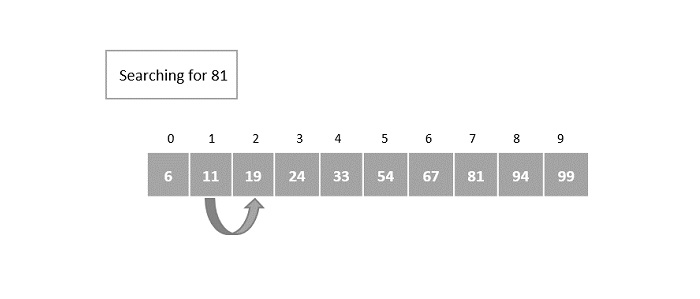
It is still not a match so it is once again incremented.
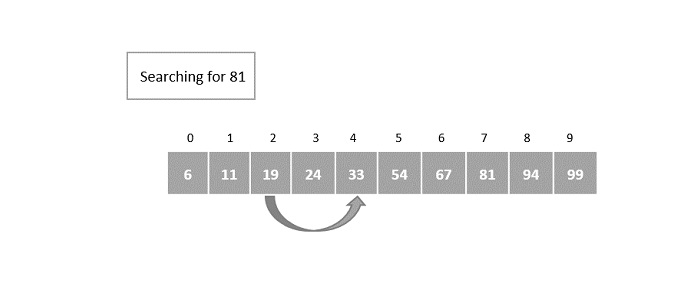
Step 3
The index is incremented in the powers of 2 again.
22 = 4 = the element in 4th index is compared with the key element and a match is not found yet.
Step 4
The index is incremented exponentially once again. This time the element in the 8th index is compared with the key element and a match is not found.
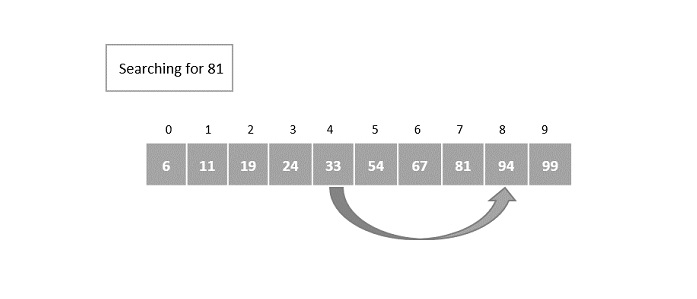
However, the element in the 8th index is greater than the key element. Hence, the binary search algorithm is applied on the current block of elements.
Step 5
The current block of elements includes the elements in the indices [4, 5, 6, 7].
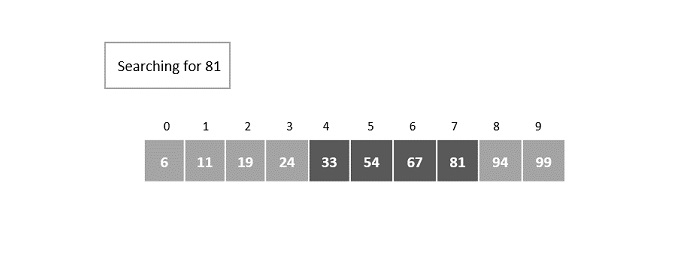
Small scale binary search is applied on this block of elements, where the mid is calculated to be the 5th element.
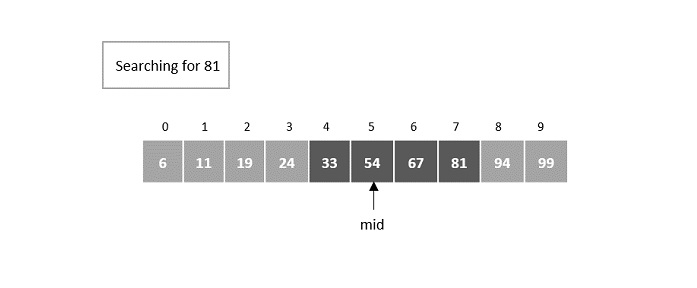
Step 6
The match is not found at the mid element and figures that the desired element is greater than the mid element. Hence, the search takes place is the right half of the block.
The mid now is set as 6th element −
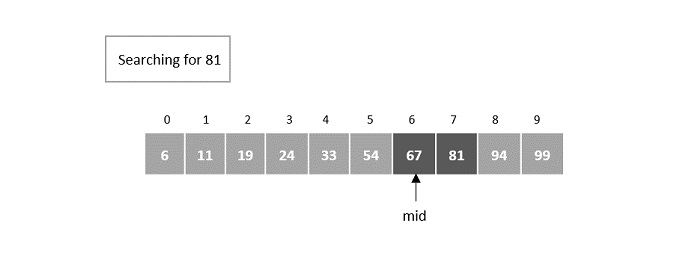
Step 7
The element is still not found at the 6th element so it now searches in the right half of the mid element.
The next mid is set as 7th element.
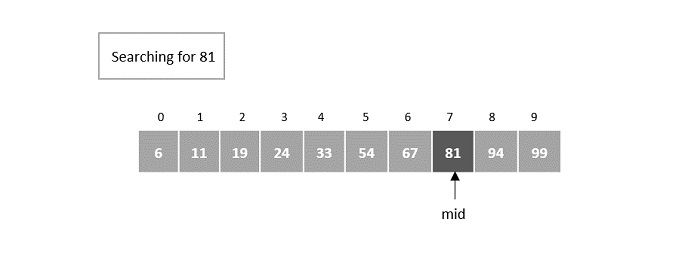
Here, the element is found at the 7th index.
Implementation
In the implementation of the exponential search algorithm, the program checks for the matches at every exponential jump in the powers of 2. If the match is found the location of the element is returned otherwise the program returns an unsuccessful search.
Once the element at an exponential jump becomes greater than the key element, a binary search is performed on the current block of elements.
In this chapter, we will look into the implementation of exponential search in four different languages.
#include <stdio.h>
#include <math.h>
int exponential_search(int[], int, int);
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
printf("Array elements are: ");
int len = sizeof(arr) / sizeof(arr[0]);
for(int j = 0; j<len; j++){
printf("%d ", arr[j]);
}
key = 67;
printf("\nThe element to be searched: %d", key);
pos = exponential_search(arr, n, key);
if(pos >= 0)
printf("\nThe element is found at %d", pos);
else
printf("\nUnsuccessful Search");
}
int exponential_search(int a[], int n, int key){
int i, m, low = 0, high = n - 1, mid;
i = 1;
m = pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = pow(2,i);
while (low <= high) {
mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
Output
Array elements are: 6 11 19 24 33 54 67 81 94 99 The element to be searched: 67 The element is found at 6
#include <iostream>
#include <cmath>
using namespace std;
int exponential_search(int[], int, int);
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
cout<<"Array elements are: ";
for(auto j : arr){
cout<<j<<" ";
}
n = 10;
key = 67;
cout<<"\nThe element to be searched: "<<key;
pos = exponential_search(arr, n, key);
if(pos >= 0)
cout << "\nThe element is found at " << pos;
else
cout << "\nUnsuccessful Search";
}
int exponential_search(int a[], int n, int key){
int i, m, low = 0, high = n - 1, mid;
i = 1;
m = pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = pow(2,i);
while (low <= high) {
mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
Output
Array elements are: 6 11 19 24 33 54 67 81 94 99 The element to be searched: 67 The element is found at 6
import java.io.*;
import java.util.Scanner;
import java.lang.Math;
public class ExponentialSearch {
public static void main(String args[]) {
int i, n, key;
int arr[] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
System.out.print("Array elements are: ");
for(int j = 0; j<arr.length; j++){
System.out.print(arr[j] + " ");
}
n = 10;
key = 67;
System.out.print("\nThe element to be searched: " + key);
int pos = exponential_search(arr, n, key);
if(pos >= 0)
System.out.print("\nThe element is found at " + pos);
else
System.out.print("\nUnsuccessful Search");
}
static int exponential_search(int a[], int n, int key) {
int i = 1;
int m = (int)Math.pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = (int)Math.pow(2,i);
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
}
Output
Array elements are: 6 11 19 24 33 54 67 81 94 99 The element to be searched: 67 The element is found at 6
import math
def exponential_search(a, n, key):
i = 1
m = int(math.pow(2, i))
if(a[0] == key):
return 0
while(a[m] <= key and m < n):
i = i + 1
m = int(math.pow(2, i))
low = 0
high = n - 1
while (low <= high):
mid = (low + high) // 2
if(a[mid] == key):
return mid
elif(a[mid] < key):
low = mid + 1
else:
high = mid - 1
return -1
arr = [6, 11, 19, 24, 33, 54, 67, 81, 94, 99]
n = len(arr);
print("Array elements are: ")
for i in range(len(arr)):
print(arr[i], end = " ")
key = 67
print("\nThe element to be searched: ", key)
index = exponential_search(arr, n, key)
if(index >= 0):
print("The element is found at index: ", (index))
else:
print("\nUnsuccessful Search")
Output
Array elements are: 6 11 19 24 33 54 67 81 94 99 The element to be searched: 67 The element is found at index: 6

To Continue Learning Please Login