Fisher-Yates Shuffle Algorithm

The Fisher-Yates Shuffle algorithm shuffles a finite sequence of elements by generating a random permutation. The possibility of every permutation occurring is equally likely. The algorithm is performed by storing the elements of the sequence in a sack and drawing each element randomly from the sack to form the shuffled sequence.

Coined after Ronald Fisher and Frank Yates, for designing the original method of the shuffle, the algorithm is unbiased. It generates all permutations in same conditions so the output achieved is nowhere influenced. However, the modern version of the Fisher-Yates Algorithm is more efficient than that of the original one.

Fisher-Yates Algorithm

The Original Method

The original method of Shuffle algorithm involved a pen and paper to generate a random permutation of a finite sequence. The algorithm to generate the random permutation is as follows −

Step 1 − Write down all the elements in the finite sequence. Declare a separate list to store the output achieved.

Step 2 − Choose an element i randomly in the input sequence and add it onto the output list. Mark the element i as visited.

Step 3 − Repeat Step 2 until all the element in the finite sequence is visited and added onto the output list randomly.

Step 4 − The output list generated after the process terminates is the random permutation generated.

The Modern Algorithm

The modern algorithm is a slightly modified version of the original fisher-yates shuffle algorithm. The main goal of the modification is to computerize the original algorithm by reducing the time complexity of the original method. The modern method is developed by Richard Durstenfeld and was popularized by Donald E. Knuth.

Therefore, the modern method makes use of swapping instead of maintaining another output list to store the random permutation generated. The time complexity is reduced to O(n) rather than O(n²). The algorithm goes as follows −

Step 1 − Write down the elements 1 to n in the finite sequence.

Step 2 − Choose an element i randomly in the input sequence and swap it with the last unvisited element in the list.

Step 3 − Repeat Step 2 until all the element in the finite sequence is visited and swapped.

Step 4 − The list generated after the process terminates is the random permutation sequence.

Pseudocode

Shuffling is done from highest index to the lowest index of the array in the following modern method pseudocode.

Fisher-Yates Shuffle (array of n elements):
for i from n−1 downto 1 do
   j ← random integer such that 0 ≤ j ≤ i
   exchange a[j] and a[i]

Shuffling is done from lowest index to the highest index of the array in the following modern method pseudocode.

Fisher-Yates Shuffle (array of n elements):
for i from 0 to n−2 do
   j ← random integer such that i ≤ j < n
   exchange a[i] and a[j]

Original Method Example

To describe the algorithm better, let us permute the the given finite sequence of the first six letters of the alphabet. Input sequence: A B C D E F.

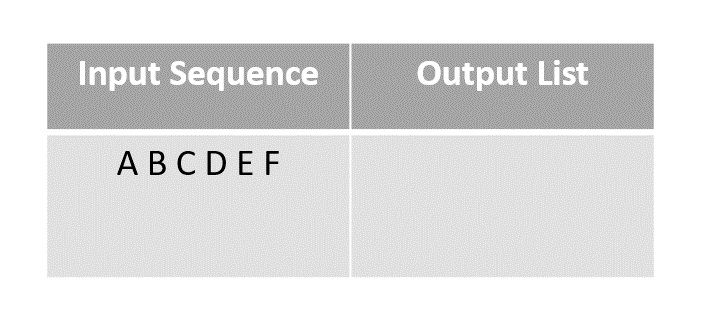
Step 1

This is called the pen and paper method. We consider an input array with the finite sequence stored and an output array to store the result.

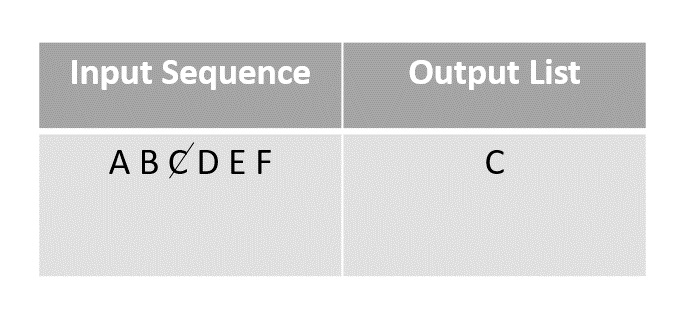
Step 2

Choose any element randomly and add it onto the output list after marking it checked. In this case, we choose element C.

Step 3

The next element chosen randomly is E which is marked and added to the output list.

Step 4

The random function then picks the next element A and adds it onto the output array after marking it visited.

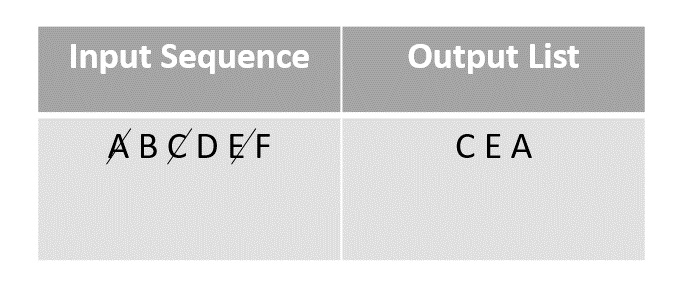
Step 5

Then F is selected from the remaining elements in the input sequence and added to the output after marking it visited.

Step 6

The next element chosen to add onto the random permutation is D. It is marked and added to the output array.

Step 7

The last element present in the input list would be B, so it is marked and added onto the output list finally.

Modern Method Example

In order to reduce time complexity of the original method, the modern algorithm is introduced. The modern method uses swapping to shuffle the sequences – for example, the algorithm works like shuffling a pack of cards by swapping their places in the original deck. Let us look at an example to understand how modern version of the Fisher-Yates algorithm works.

Step 1

Consider first few letters of the alphabet as an input and shuffle them using the modern method.

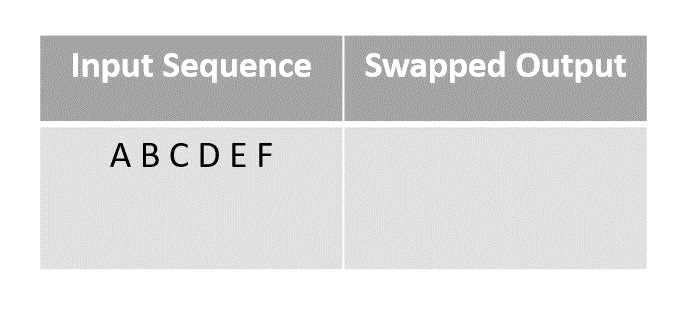
Step 2

Randomly choosing the element D and swapping it with the last unmarked element in the sequence, in this case F.

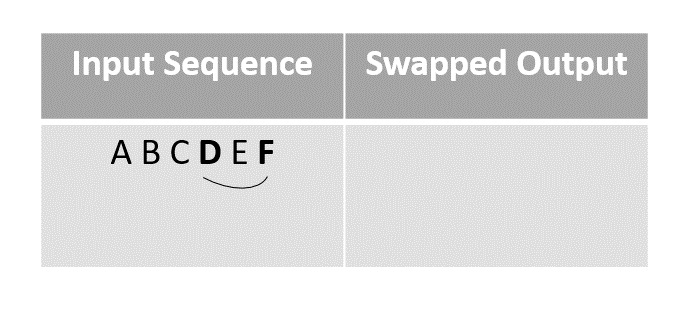
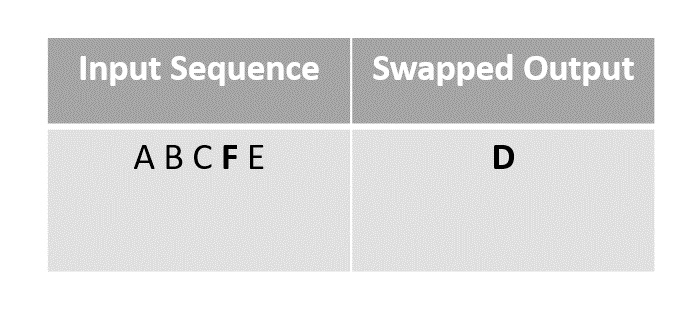
Step 3

For the next step we choose element B to swap with the last unmarked element ‘E’ since F had been moved to D’s place after swapping in the previous step.

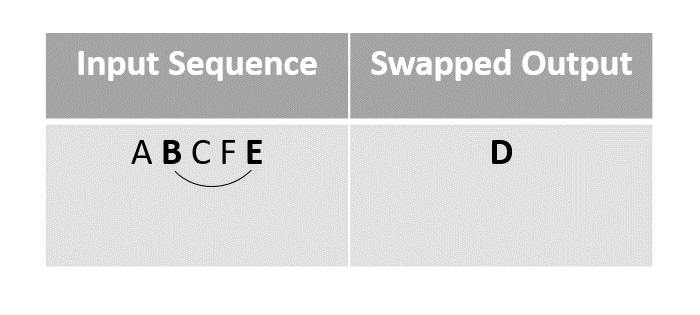
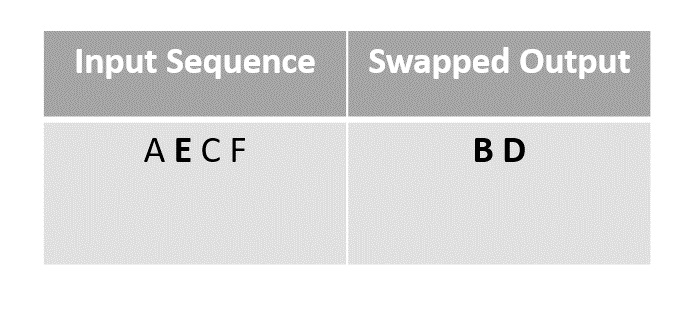
Step 4

We next swap the element A with F, since it is the last unmarked element in the list.

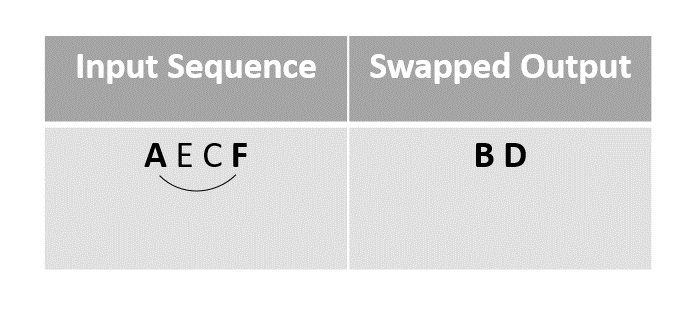
Step 5

Then the element F is swapped with the last unmarked element C.

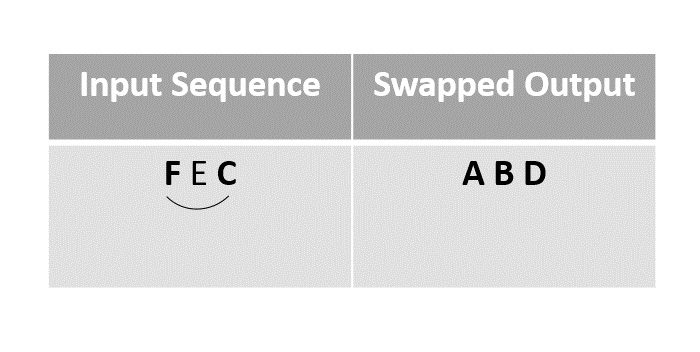
Step 6

The remaining elements in the sequence could be swapped finally, but since the random function chose E as the element it is left as it is.

Step 7

The remaining element C is left as it is without swapping.

The array obtained after swapping is the final output array.

Example

Following are the implementations of the above approach in various programming langauges −

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(char arr[], char n) {
    char output[n];  // Create an output array to store the shuffled elements
    char visited[n]; // Create a boolean array to keep track of visited elements
    // Initialize the visited array with zeros (false)
    for (char i = 0; i < n; i++) {
        visited[i] = 0;
    }
    // Perform the shuffle algorithm
    for (char i = 0; i < n; i++) {
        char j = rand() % n; // Generate a random index in the input array
        while (visited[j]) { // Find the next unvisited index
            j = rand() % n;
        }
        output[i] = arr[j]; // Add the element at the chosen index to the output array
        visited[j] = 1;     // Mark the element as visited
    }
    // Copy the shuffled elements back to the original array
    for (char i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}
int main() {
    char arr[] = {'A', 'B', 'C', 'D', 'E', 'F'};
    char n = sizeof(arr) / sizeof(arr[0]);

    srand(time(NULL)); // Seed the random number generator with the current time
    fisherYatesShuffle(arr, n); // Call the shuffle function
    printf("Shuffled array: ");
    for (char i = 0; i < n; i++) {
        printf("%c ", arr[i]); // Print the shuffled array
    }
    printf("\n");
    return 0;
}

Shuffled array: A B F D E C 

#include <iostream>
#include <vector>
#include <algorithm>
#include <random>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(std::vector<char>& arr) {
    std::vector<char> output; // Create an output vector to store the shuffled elements
    std::vector<bool> visited(arr.size(), false); // Create a boolean vector to keep track of visited elements
    // Perform the shuffle algorithm
    for (char i = 0; i < arr.size(); i++) {
        char j = rand() % arr.size(); // Generate a random index in the input vector
        while (visited[j]) { // Find the next unvisited index
            j = rand() % arr.size();
        }
        output.push_back(arr[j]); // Add the element at the chosen index to the output vector
        visited[j] = true; // Mark the element as visited
    }
    arr = output; // Copy the shuffled elements back to the original vector
}
int main() {
    std::vector<char> arr = {'A', 'B', 'C', 'D', 'E', 'F'};
    srand(time(NULL)); // Seed the random number generator with the current time
    fisherYatesShuffle(arr); // Call the shuffle function
    std::cout << "Shuffled array: ";
    for (char c : arr) {
        std::cout << c << " "; // Print the shuffled array
    }
    std::cout << std::endl;
    return 0;
}

Shuffled array: D B A F C E

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class FisherYatesShuffle {
    // Function to perform Fisher-Yates Shuffle using the original method
    public static List<Character> fisherYatesShuffle(List<Character> arr) {
        List<Character> output = new ArrayList<>(); // Create an output list to store the shuffled elements
        boolean[] visited = new boolean[arr.size()]; // Create a boolean array to keep track of visited elements
        // Perform the shuffle algorithms
        for (int i = 0; i < arr.size(); i++) {
            int j = new Random().nextInt(arr.size()); // Generate a random index in the input list
            while (visited[j]) { // Find the next unvisited index
                j = new Random().nextInt(arr.size());
            }
            output.add(arr.get(j)); // Add the element at the chosen index to the output list
            visited[j] = true; // Mark the element as visited
        }
        return output;
    }
    public static void main(String[] args) {
        List<Character> arr = List.of('A', 'B', 'C', 'D', 'E', 'F');
        Random rand = new Random(); // Seed the random number generator with the current time
        List<Character> shuffledArray = fisherYatesShuffle(arr); // Call the shuffle function
        System.out.print("Shuffled array: ");
        for (char c : shuffledArray) {
            System.out.print(c + " "); // Print the shuffled array
        }
        System.out.println();
    }
}

Shuffled array: D B E C A F 

import random
# Function to perform Fisher-Yates Shuffle using the original method
def fisherYatesShuffle(arr):
    output = []  # Create an output list to store the shuffled elements
    visited = [False] * len(
        arr)  # Create a boolean list to keep track of visited elements
    # Perform the shuffle algorithm
    for i in range(len(arr)):
        j = random.randint(0,
                           len(arr) -
                           1)  # Generate a random index in the input list
        while visited[j]:  # Find the next unvisited index
            j = random.randint(0, len(arr) - 1)
        output.append(
            arr[j])  # Add the element at the chosen index to the output list
        visited[j] = True  # Mark the element as visited
    return output
if __name__ == "__main__":
    arr = ['A', 'B', 'C', 'D', 'E', 'F']
    random.seed()  # Seed the random number generator with the current time
    shuffled_array = fisherYatesShuffle(arr)  # Call the shuffle function
    print("Shuffled array:", shuffled_array)  # Print the shuffled array

Shuffled array: ['D', 'C', 'A', 'B', 'F', 'E']