Design and Analysis - Interpolation Search

Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.

Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of Ο(n) whereas binary search has Ο(log n).

There are cases where the location of target data may be known in advance. For example, in case of a telephone directory, if we want to search the telephone number of “Morpheus”. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored.

Positioning in Binary Search

In binary search, if the desired data is not found then the rest of the list is divided in two parts, lower and higher. The search is carried out in either of them.

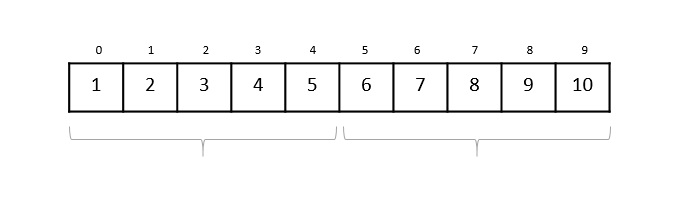
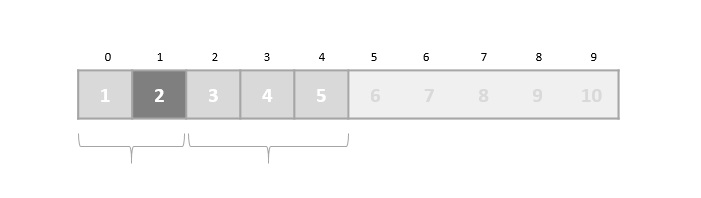
Even when the data is sorted, binary search does not take advantage to probe the position of the desired data.

Position Probing in Interpolation Search

Interpolation search finds a particular item by computing the probe position. Initially, the probe position is the position of the middle most item of the collection.

If a match occurs, then the index of the item is returned. To split the list into two parts, we use the following method −

$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$

where −

A = list
Lo = Lowest index of the list
Hi = Highest index of the list
A[n] = Value stored at index n in the list

If the middle item is greater than the item, then the probe position is again calculated in the sub-array to the right of the middle item. Otherwise, the item is searched in the sub-array to the left of the middle item. This process continues on the sub-array as well until the size of subarray reduces to zero.

Interpolation Search Algorithm

As it is an improvisation of the existing BST algorithm, we are mentioning the steps to search the 'target' data value index, using position probing −

Step 1 − Start searching data from middle of the list.

Step 2 − If it is a match, return the index of the item, and exit.

Step 3 − If it is not a match, probe position.

Step 4 − Divide the list using probing formula and find the new middle.

Step 5 − If data is greater than middle, search in higher sub-list.

Step 6 − If data is smaller than middle, search in lower sub-list.

Step 7 − Repeat until match.

Pseudocode

A → Array list
N → Size of A
X → Target Value

Procedure Interpolation_Search()

   Set Lo → 0
   Set Mid → -1
   Set Hi → N-1

   While X does not match
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if

      Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])

      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While
End Procedure

Analysis

Runtime complexity of interpolation search algorithm is Ο(log (log n)) as compared to Ο(log n) of BST in favorable situations.

Example

To understand the step-by-step process involved in the interpolation search, let us look at an example and work around it.

Consider an array of sorted elements given below −

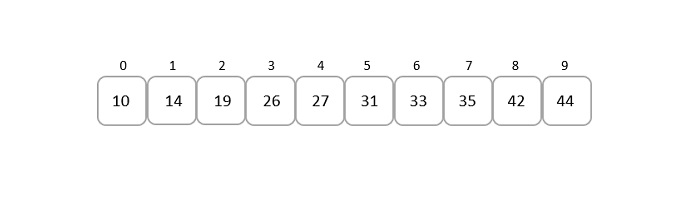
Let us search for the element 19.

Solution

Unlike binary search, the middle point in this approach is chosen using the formula −

$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$

So in this given array input,

Lo = 0, A[Lo] = 10
Hi = 9, A[Hi] = 44
X = 19

Applying the formula to find the middle point in the list, we get

$$mid\, =\, 0\, +\, \frac{\left ( 9\, -\, 0 \right )\ast \left ( 19\, -\, 10 \right )}{44\, -\, 10}$$

$$mid\, =\, \frac{9\ast 9}{34}$$

$$mid\, =\, \frac{81}{34}\,=\,2.38$$

Since, mid is an index value, we only consider the integer part of the decimal. That is, mid = 2.

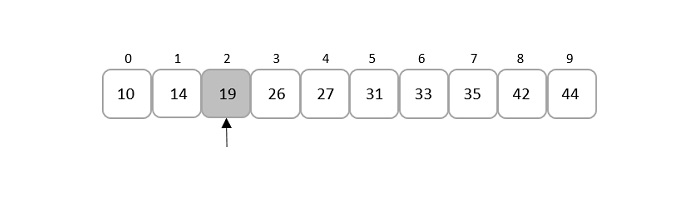
Comparing the key element given, that is 19, to the element present in the mid index, it is found that both the elements match.

Therefore, the element is found at index 2.

Example

Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in sorted and equally distributed form.

#include<stdio.h>
#define MAX 10

// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
   int lo = 0;
   int hi = MAX - 1;
   int mid = -1;
   int comparisons = 1;
   int index = -1;
   while(lo <= hi) {
      printf("\nComparison %d \n" , comparisons ) ;
      printf("lo : %d, list[%d] = %d\n", lo, lo, list[lo]);
      printf("hi : %d, list[%d] = %d\n", hi, hi, list[hi]);
      comparisons++;
      
      // probe the mid point
      mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
      printf("mid = %d\n",mid);
      
      // data found
      if(list[mid] == data) {
         index = mid;
         break;
      } else {
         if(list[mid] < data) {
            
            // if data is larger, data is in upper half
            lo = mid + 1;
         } else {
            
            // if data is smaller, data is in lower half
            hi = mid - 1;
         }
      }
   }
   printf("\nTotal comparisons made: %d", --comparisons);
   return index;
}
int main(){
   
   //find location of 33
   int location = interpolation_search(33);
   
   // if element was found
   if(location != -1)
      printf("\nElement found at location: %d" ,(location+1));
   else
      printf("Element not found.");
   return 0;
}

Comparison 1 
lo : 0, list[0] = 10
hi : 9, list[9] = 44
mid = 6

Total comparisons made: 1
Element found at location: 7

#include<iostream>
using namespace std;
#define MAX 10

// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
   int lo = 0;
   int hi = MAX - 1;
   int mid = -1;
   int comparisons = 1;
   int index = -1;
   while(lo <= hi) {
      cout << "\nComparison " << comparisons << endl;
      cout << "lo : " << lo << " list[" << lo << "] = " << list[lo] << endl;
      cout << "hi : " << hi << " list[" << hi << "] = " << list[hi] << endl;
      comparisons++;
      
      // probe the mid point
      mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
      cout << "mid = " << mid;
      
      // data found
      if(list[mid] == data) {
         index = mid;
         break;
      } else {
         if(list[mid] < data) {
            
            // if data is larger, data is in upper half
            lo = mid + 1;
         } else {
            
            // if data is smaller, data is in lower half
            hi = mid - 1;
         }
      }
   }
   cout << "\nTotal comparisons made: " << (--comparisons);
   return index;
}
int main(){
   
   //find location of 33
   int location = interpolation_search(33);
   
   // if element was found
   if(location != -1)
      cout << "\nElement found at location: " << (location+1);
   else
      cout << "Element not found.";
   return 0;
}

Comparison 1
lo : 0 list[0] = 10
hi : 9 list[9] = 44
mid = 6
Total comparisons made: 1
Element found at location: 7

import java.io.*;
public class InterpolationSearch {
   static int interpolation_search(int data, int[] list) {
      int lo = 0;
      int hi = list.length - 1;
      int mid = -1;
      int comparisons = 1;
      int index = -1;
      while(lo <= hi) {
         System.out.println("\nComparison " + comparisons);
         System.out.println("lo : " + lo + " list[" + lo + "] = " + list[lo]);
         System.out.println("hi : " + hi + " list[" + hi + "] = " + list[hi]);
         comparisons++;
         
         // probe the mid point
         mid = lo + (((hi - lo) * (data - list[lo])) / (list[hi] - list[lo]));
         System.out.println("mid = " + mid);
         
         // data found
         if(list[mid] == data) {
            index = mid;
            break;
         } else {
            if(list[mid] < data) {
               
               // if data is larger, data is in upper half
               lo = mid + 1;
            } else {
               
               // if data is smaller, data is in lower half
               hi = mid - 1;
            }
         }
      }
      System.out.println("\nTotal comparisons made: " + (--comparisons));
      return index;
   }
   public static void main(String args[]) {
      int[] list = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
      
      //find location of 33
      int location = interpolation_search(33, list);
      
      // if element was found
      if(location != -1)
         System.out.println("\nElement found at location: " + (location+1));
      else
         System.out.println("Element not found.");
   }
}

Comparison 1
lo : 0 list[0] = 10
hi : 9 list[9] = 44
mid = 6
Total comparisons made: 1
Element found at location: 7

def interpolation_search( data, arr):
   lo = 0
   hi = len(arr) - 1
   mid = -1
   comparisons = 1
   index = -1
   while(lo <= hi):
      print("\nComparison ", comparisons)
      print("lo : ", lo)
      print("list[", lo, "] = ")
      print(arr[lo])
      print("hi : ", hi)
      print("list[", hi, "] = ")
      print(arr[hi])
      comparisons = comparisons + 1

      #probe the mid point
      mid = lo + (((hi - lo) * (data - arr[lo])) // (arr[hi] - arr[lo]))
      print("mid = ", mid)

      #data found
      if(arr[mid] == data):
         index = mid
         break
      else:
         if(arr[mid] < data):
            
            #if data is larger, data is in upper half
            lo = mid + 1
         else:

            #if data is smaller, data is in lower half
            hi = mid - 1
   print("\nTotal comparisons made: ")
   print(comparisons-1)
   return index

arr = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
#find location of 33
location = interpolation_search(33, arr)

#if element was found
if(location != -1):
   print("\nElement found at location: ", (location+1))
else:
   print("Element not found.")

Comparison  1
lo :  0
list[ 0 ] = 
10
hi :  9
list[ 9 ] = 
44
mid =  6

Total comparisons made: 
1

Element found at location:  7

Kickstart Your Career

Get certified by completing the course

Get Started