
- Design and Analysis of Algorithms
- Home
- Basics of Algorithms
- DAA - Introduction to Algorithms
- DAA - Analysis of Algorithms
- DAA - Methodology of Analysis
- DAA - Asymptotic Notations & Apriori Analysis
- DAA - Time Complexity
- DAA - Master's Theorem
- DAA - Space Complexities
- Divide & Conquer
- DAA - Divide & Conquer Algorithm
- DAA - Max-Min Problem
- DAA - Merge Sort Algorithm
- DAA - Strassen's Matrix Multiplication
- DAA - Karatsuba Algorithm
- DAA - Towers of Hanoi
- Greedy Algorithms
- DAA - Greedy Algorithms
- DAA - Travelling Salesman Problem
- DAA - Prim's Minimal Spanning Tree
- DAA - Kruskal's Minimal Spanning Tree
- DAA - Dijkstra's Shortest Path Algorithm
- DAA - Map Colouring Algorithm
- DAA - Fractional Knapsack
- DAA - Job Sequencing with Deadline
- DAA - Optimal Merge Pattern
- Dynamic Programming
- DAA - Dynamic Programming
- DAA - Matrix Chain Multiplication
- DAA - Floyd Warshall Algorithm
- DAA - 0-1 Knapsack Problem
- DAA - Longest Common Subsequence Algorithm
- DAA - Travelling Salesman Problem using Dynamic Programming
- Randomized Algorithms
- DAA - Randomized Algorithms
- DAA - Randomized Quick Sort Algorithm
- DAA - Karger's Minimum Cut Algorithm
- DAA - Fisher-Yates Shuffle Algorithm
- Approximation Algorithms
- DAA - Approximation Algorithms
- DAA - Vertex Cover Problem
- DAA - Set Cover Problem
- DAA - Travelling Salesperson Approximation Algorithm
- Sorting Techniques
- DAA - Bubble Sort Algorithm
- DAA - Insertion Sort Algorithm
- DAA - Selection Sort Algorithm
- DAA - Shell Sort Algorithm
- DAA - Heap Sort Algorithm
- DAA - Bucket Sort Algorithm
- DAA - Counting Sort Algorithm
- DAA - Radix Sort Algorithm
- DAA - Quick Sort Algorithm
- Searching Techniques
- DAA - Searching Techniques Introduction
- DAA - Linear Search
- DAA - Binary Search
- DAA - Interpolation Search
- DAA - Jump Search
- DAA - Exponential Search
- DAA - Fibonacci Search
- DAA - Sublist Search
- DAA - Hash Table
- Graph Theory
- DAA - Shortest Paths
- DAA - Multistage Graph
- DAA - Optimal Cost Binary Search Trees
- Heap Algorithms
- DAA - Binary Heap
- DAA - Insert Method
- DAA - Heapify Method
- DAA - Extract Method
- Complexity Theory
- DAA - Deterministic vs. Nondeterministic Computations
- DAA - Max Cliques
- DAA - Vertex Cover
- DAA - P and NP Class
- DAA - Cook's Theorem
- DAA - NP Hard & NP-Complete Classes
- DAA - Hill Climbing Algorithm
- DAA Useful Resources
- DAA - Quick Guide
- DAA - Useful Resources
- DAA - Discussion
Shortest Path Algorithms
Dijkstra’s Algorithm
Dijkstra’s algorithm solves the single-source shortest-paths problem on a directed weighted graph G = (V, E), where all the edges are non-negative (i.e., w(u, v) ≥ 0 for each edge (u, v) Є E).
In the following algorithm, we will use one function Extract-Min(), which extracts the node with the smallest key.
Algorithm: Dijkstra’s-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
S := Ф
Q := G.V
while Q ≠ Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v.∏ := u
Analysis
The complexity of this algorithm is fully dependent on the implementation of Extract-Min function. If extract min function is implemented using linear search, the complexity of this algorithm is O(V2 + E).
In this algorithm, if we use min-heap on which Extract-Min() function works to return the node from Q with the smallest key, the complexity of this algorithm can be reduced further.
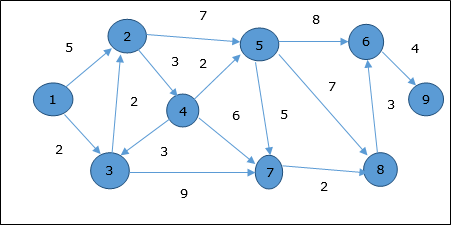
Example
Let us consider vertex 1 and 9 as the start and destination vertex respectively. Initially, all the vertices except the start vertex are marked by ∞ and the start vertex is marked by 0.
| Vertex | Initial | Step1 V1 | Step2 V3 | Step3 V2 | Step4 V4 | Step5 V5 | Step6 V7 | Step7 V8 | Step8 V6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
Hence, the minimum distance of vertex 9 from vertex 1 is 20. And the path is
1→ 3→ 7→ 8→ 6→ 9
This path is determined based on predecessor information.
Example
Following are the implementations of the above approach in various programming languages −
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#include <string.h>
#define MAX_VERTICES 10
// Structure to represent a graph edge
struct Edge {
int dest;
int weight;
};
// Dijkstra's algorithm to find the shortest path from source to all vertices
void dijkstra(int graph[MAX_VERTICES][MAX_VERTICES], int num_vertices, int src, int dist[], int prev[]) {
bool visited[MAX_VERTICES] = {false}; // Array to keep track of visited vertices
// Initialization
for (int i = 0; i < num_vertices; i++) {
dist[i] = INT_MAX; // Set distance of each vertex to infinity
prev[i] = -1; // Initialize the predecessor of each vertex to -1
}
dist[src] = 0; // Distance from source to itself is 0
while (true) {
int u = -1;
int minDist = INT_MAX;
// Find the vertex with the minimum distance from the set of vertices not yet visited
for (int i = 0; i < num_vertices; i++) {
if (!visited[i] && dist[i] < minDist) {
u = i;
minDist = dist[i];
}
}
if (u == -1) {
break; // If all vertices have been visited, exit the loop
}
visited[u] = true; // Mark the vertex as visited
// Update dist[v] for all adjacent vertices of u
for (int v = 0; v < num_vertices; v++) {
if (!visited[v] && graph[u][v] != 0 && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
prev[v] = u; // Update the predecessor of vertex v to u
}
}
}
}
int main() {
// Sample graph represented as an adjacency matrix
int graph[MAX_VERTICES][MAX_VERTICES] = {
{0, 0, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 11, 0, 0, 0},
{0, 2, 0, 2, 7, 9, 0, 0, 0, 0},
{0, 0, 2, 0, 7, 9, 0, 0, 1, 0},
{0, 0, 7, 7, 0, 9, 0, 0, 0, 0},
{0, 0, 9, 9, 9, 0, 2, 0, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 6},
{0, 0, 0, 1, 0, 0, 0, 1, 0, 6},
{0, 0, 0, 0, 0, 0, 0, 6, 6, 0}
};
int num_vertices = 10;
int source_vertex = 0;
int dist[MAX_VERTICES];
int prev[MAX_VERTICES];
dijkstra(graph, num_vertices, source_vertex, dist, prev);
int target_vertex = 8;
int path[MAX_VERTICES];
int current_vertex = target_vertex;
int path_length = 0;
// Construct the path from the source to the target vertex using the predecessor array
while (current_vertex != -1) {
path[path_length++] = current_vertex;
current_vertex = prev[current_vertex];
}
// Print the shortest distance and the path from the source to the target vertex
printf("The minimum distance of vertex %d from vertex %d is %d.\n", target_vertex, source_vertex, dist[target_vertex]);
printf("The path is ");
for (int i = path_length - 1; i >= 0; i--) {
printf("%d->", path[i]);
}
return 0;
}
Output
The minimum distance of vertex 8 from vertex 0 is 5. The path is 0->2->3->8->
#include <iostream>
#include <unordered_map>
#include <vector>
#include <limits>
// Dijkstra's algorithm to find the shortest path from source to all vertices
std::pair<std::unordered_map<std::string, int>, std::unordered_map<std::string, std::string>> dijkstra(std::unordered_map<std::string, std::unordered_map<std::string, int>>& graph, std::string src) {
std::unordered_map<std::string, int> dist; // Dictionary to store the shortest distance from source to vertex
std::unordered_map<std::string, bool> visited; // Dictionary to keep track of visited vertices
std::unordered_map<std::string, std::string> prev; // Dictionary to store the predecessor of each vertex in the shortest path
// Initialization
for (const auto& vertex : graph) {
dist[vertex.first] = std::numeric_limits<int>::max(); // Set distance of each vertex to infinity
visited[vertex.first] = false; // Mark all vertices as not visited
prev[vertex.first] = ""; // Initialize the predecessor of each vertex to an empty string
}
dist[src] = 0; // Distance from source to itself is 0
while (true) {
std::string u;
int minDist = std::numeric_limits<int>::max();
// Find the vertex with the minimum distance from the set of vertices not yet visited
for (const auto& vertex : graph) {
if (!visited[vertex.first] && dist[vertex.first] < minDist) {
u = vertex.first;
minDist = dist[vertex.first];
}
}
visited[u] = true; // Mark the vertex as visited
// Update dist[v] for all adjacent vertices of u
for (const auto& neighbor : graph[u]) {
std::string v = neighbor.first;
int weight = neighbor.second;
if (!visited[v] && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
prev[v] = u; // Update the predecessor of vertex v to u
}
}
// If all vertices have been visited, exit the loop
bool allVisited = true;
for (const auto& vertex : visited) {
if (!vertex.second) {
allVisited = false;
break;
}
}
if (allVisited) {
break;
}
}
return std::make_pair(dist, prev);
}
int main() {
// Sample graph represented as an adjacency list (unordered_map of unordered_maps)
std::unordered_map<std::string, std::unordered_map<std::string, int>> graph = {
{"1", {{"3", 2}}},
{"3", {{"1", 2}, {"7", 11}, {"2", 2}}},
{"2", {{"3", 2}, {"4", 7}, {"5", 9}}},
{"4", {{"2", 7}, {"5", 9}, {"7", 1}}},
{"5", {{"2", 9}, {"4", 9}, {"6", 2}}},
{"7", {{"3", 11}, {"4", 1}, {"8", 1}}},
{"8", {{"7", 1}, {"6", 7}, {"9", 6}}},
{"6", {{"5", 2}, {"8", 7}, {"9", 6}}},
{"9", {{"8", 6}, {"6", 6}}}
};
std::string source_vertex = "1";
auto result = dijkstra(graph, source_vertex);
std::unordered_map<std::string, int> distances = result.first;
std::unordered_map<std::string, std::string> predecessors = result.second;
std::string target_vertex = "9";
std::vector<std::string> path;
std::string current_vertex = target_vertex;
// Construct the path from the source to the target vertex using the predecessor map
while (!current_vertex.empty()) {
path.insert(path.begin(), current_vertex); // Insert the current vertex at the beginning of the path
current_vertex = predecessors[current_vertex]; // Move to the predecessor of the current vertex
}
// Create a string representation of the path
std::string path_string = "";
for (const auto& vertex : path) {
path_string += vertex + "->"; // Append each vertex to the path string followed by "->"
}
path_string = path_string.substr(0, path_string.length() - 2); // Remove the last "->" from the path string
// Print the shortest distance and the path from the source to the target vertex
std::cout << "The minimum distance of vertex 9 from vertex 1 is " << distances[target_vertex] << "." << std::endl;
std::cout << "The path is " << path_string << "." << std::endl;
return 0;
}
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 1->3->2->4->7->8->9.
import java.util.*;
public class DijkstraAlgorithm {
public static Map<String, Integer> dijkstra(Map<String, Map<String, Integer>> graph, String src) {
Map<String, Integer> dist = new HashMap<>();
Map<String, Boolean> visited = new HashMap<>();
Map<String, String> prev = new HashMap<>();
for (String vertex : graph.keySet()) {
dist.put(vertex, Integer.MAX_VALUE);
visited.put(vertex, false);
prev.put(vertex, null);
}
dist.put(src, 0);
while (true) {
String u = null;
int minDistance = Integer.MAX_VALUE;
for (String vertex : graph.keySet()) {
if (!visited.get(vertex) && dist.get(vertex) < minDistance) {
u = vertex;
minDistance = dist.get(vertex);
}
}
if (u == null) {
break; // All vertices have been visited
}
visited.put(u, true);
if (graph.containsKey(u)) {
for (Map.Entry<String, Integer> neighbor : graph.get(u).entrySet()) {
String v = neighbor.getKey();
int weight = neighbor.getValue();
if (!visited.get(v) && dist.get(u) != Integer.MAX_VALUE && dist.get(u) + weight < dist.get(v)) {
dist.put(v, dist.get(u) + weight);
prev.put(v, u);
}
}
}
}
return dist;
}
public static List<String> reconstructPath(Map<String, String> prev, String target) {
List<String> path = new ArrayList<>();
String current = target;
while (current != null) {
path.add(0, current);
current = prev.get(current);
}
return path;
}
public static void main(String[] args) {
// Sample graph represented as an adjacency list (map of maps)
Map<String, Map<String, Integer>> graph = new HashMap<>();
graph.put("1", Map.of("3", 2));
graph.put("3", Map.of("1", 2, "7", 11, "2", 2));
graph.put("2", Map.of("3", 2, "4", 7, "5", 9));
graph.put("4", Map.of("2", 7, "5", 9, "7", 1));
graph.put("5", Map.of("2", 9, "4", 9, "6", 2));
graph.put("7", Map.of("3", 11, "4", 1, "8", 1));
graph.put("8", Map.of("7", 1, "6", 7, "9", 6));
graph.put("6", Map.of("5", 2, "8", 7, "9", 6));
graph.put("9", Map.of("8", 6, "6", 6));
String sourceVertex = "1";
Map<String, Integer> distances = dijkstra(graph, sourceVertex);
Map<String, String> prev = new HashMap<>(); // Store predecessors for path reconstruction
// Print the minimum distance from vertex 1 to vertex 9
String targetVertex = "9";
System.out.println("The minimum distance of vertex 9 from vertex 1 is " + distances.get(targetVertex) + ".");
// Reconstruct and print the path
List<String> path = reconstructPath(prev, targetVertex);
System.out.print("The path is ");
for (int i = 0; i < path.size() - 1; i++) {
System.out.print(path.get(i) + "->");
}
System.out.println(path.get(path.size() - 1) + ".");
}
}
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 9.
# Dijkstra's algorithm to find the shortest path from source to all vertices
def dijkstra(graph, src):
dist = {vertex: float('inf') for vertex in graph} # Dictionary to store the shortest distance from source to vertex
visited = {vertex: False for vertex in graph} # Dictionary to keep track of visited vertices
prev = {vertex: None for vertex in graph} # Dictionary to store the predecessor of each vertex in the shortest path
dist[src] = 0 # Distance from source to itself is 0
while True:
# Find the vertex with the minimum distance from the set of vertices not yet visited
u = min((vertex for vertex in graph if not visited[vertex]), key=lambda vertex: dist[vertex])
# Mark the vertex as visited
visited[u] = True
# Update dist[v] for all adjacent vertices of u
for v, weight in graph[u].items():
if not visited[v] and dist[u] + weight < dist[v]:
dist[v] = dist[u] + weight
prev[v] = u
# If all vertices have been visited, exit the loop
if all(visited.values()):
break
return dist, prev
# Example usage:
if __name__ == "__main__":
# Sample graph represented as an adjacency list (dictionary of dictionaries)
graph = {
'1': {'3': 2},
'3': {'1': 2, '7': 11, '2': 2},
'2': {'3': 2, '4': 7, '5': 9},
'4': {'2': 7, '5': 9, '7': 1},
'5': {'2': 9, '4': 9, '6': 2},
'7': {'3': 11, '4': 1, '8': 1},
'8': {'7': 1, '6': 7, '9': 6},
'6': {'5': 2, '8': 7, '9': 6},
'9': {'8': 6, '6': 6}
}
source_vertex = '1'
distances, predecessors = dijkstra(graph, source_vertex)
# Print the shortest path and distance from vertex 1 to vertex 9
target_vertex = '9'
path = []
current_vertex = target_vertex
while current_vertex is not None:
path.insert(0, current_vertex)
current_vertex = predecessors[current_vertex]
path_string = '->'.join(path)
print(f"The minimum distance of vertex 9 from vertex 1 is {distances[target_vertex]}.")
print(f"The path is {path_string}.")
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 1->3->2->4->7->8->9.
Bellman Ford Algorithm
This algorithm solves the single source shortest path problem of a directed graph G = (V, E) in which the edge weights may be negative. Moreover, this algorithm can be applied to find the shortest path, if there does not exist any negative weighted cycle.
Algorithm: Bellman-Ford-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v.∏ := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
Analysis
The first for loop is used for initialization, which runs in O(V) times. The next for loop runs |V - 1| passes over the edges, which takes O(E) times.
Hence, Bellman-Ford algorithm runs in O(V, E) time.
Example
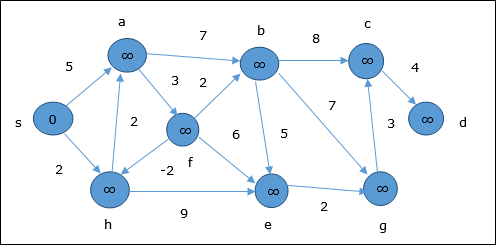
The following example shows how Bellman-Ford algorithm works step by step. This graph has a negative edge but does not have any negative cycle, hence the problem can be solved using this technique.
At the time of initialization, all the vertices except the source are marked by ∞ and the source is marked by 0.
In the first step, all the vertices which are reachable from the source are updated by minimum cost. Hence, vertices a and h are updated.
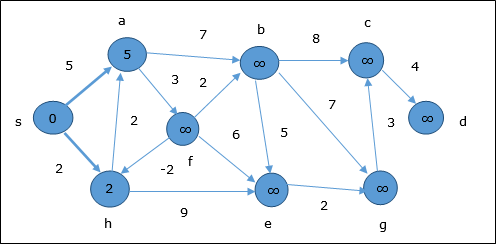
In the next step, vertices a, b, f and e are updated.
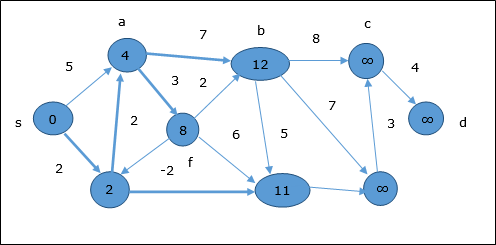
Following the same logic, in this step vertices b, f, c and g are updated.
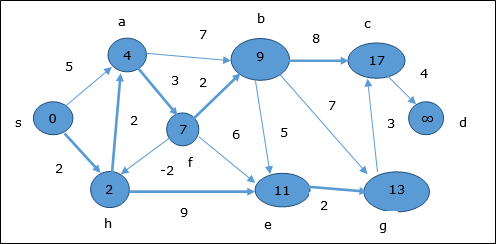
Here, vertices c and d are updated.
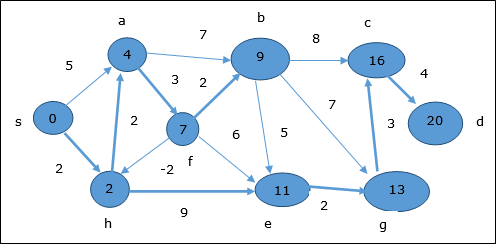
Hence, the minimum distance between vertex s and vertex d is 20.
Based on the predecessor information, the path is s→ h→ e→ g→ c→ d
Example
Following are the implementations of the above approach in various programming languages −
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 6 // Number of vertices
// Function to implement the Bellman-Ford algorithm
bool bellmanFord(int graph[V][V], int src, int distance[], int predecessor[]) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = INT_MAX;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass = 1; pass < V; pass++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
int main() {
int graph[V][V] = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int distance[V];
int predecessor[V];
// Call the bellmanFord function
bool hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
printf("Graph contains negative-weight cycle.\n");
} else {
printf("Shortest distances from vertex %d:\n", source);
for (int i = 0; i < V; i++) {
printf("Vertex %d: Distance = %d, Predecessor = %d\n", i, distance[i], predecessor[i]);
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
printf("Shortest distance from vertex %d to vertex %d: %d\n", source, destination, distance[destination]);
}
return 0;
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
#include <iostream>
#include <limits.h>
#define V 6 // Number of vertices
// Function to implement the Bellman-Ford algorithm
bool bellmanFord(int graph[V][V], int src, int distance[], int predecessor[]) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = INT_MAX;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass = 1; pass < V; pass++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
int main() {
int graph[V][V] = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int distance[V];
int predecessor[V];
// Call the bellmanFord function
bool hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
std::cout << "Graph contains negative-weight cycle." << std::endl;
} else {
std::cout << "Shortest distances from vertex " << source << ":" << std::endl;
for (int i = 0; i < V; i++) {
std::cout << "Vertex " << i << ": Distance = " << distance[i] << ", Predecessor = " << predecessor[i] << std::endl;
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
std::cout<< "Shortest distance from vertex " << source << " to vertex " << destination << ": " << distance[destination]<<std::endl;
}
return 0;
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
import java.util.Arrays;
public class BellmanFordAlgorithm {
static final int V = 6; // Number of vertices
// Function to implement the Bellman-Ford algorithm
static boolean bellmanFord(int[][] graph, int src, int[] distance, int[] predecessor) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = Integer.MAX_VALUE;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass_num = 1; pass_num < V; pass_num++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
public static void main(String[] args) {
int[][] graph = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int[] distance = new int[V];
int[] predecessor = new int[V];
// Call the bellmanFord function
boolean hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
System.out.println("Graph contains negative-weight cycle.");
} else {
System.out.println("Shortest distances from vertex " + source + ":");
for (int i = 0; i < V; i++) {
System.out.println("Vertex " + i + ": Distance = " + distance[i] + ", Predecessor = " + predecessor[i]);
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
System.out.println("Shortest distance from vertex " + source + " to vertex " + destination + ": " + distance[destination]);
}
}
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
V = 6 # Number of vertices
# Function to implement the Bellman-Ford algorithm
def bellman_ford(graph, src, distance, predecessor):
# Step 1: Initialization
for i in range(V):
distance[i] = float('inf')
predecessor[i] = -1
distance[src] = 0
# Step 2: Relaxation of edges for |V-1| passes
for pass_num in range(V - 1):
for u in range(V):
for v in range(V):
if graph[u][v] != 0 and distance[u] != float('inf') and distance[v] > distance[u] + graph[u][v]:
distance[v] = distance[u] + graph[u][v]
predecessor[v] = u
# Step 3: Check for negative-weight cycles
for u in range(V):
for v in range(V):
if graph[u][v] != 0 and distance[u] != float('inf') and distance[v] > distance[u] + graph[u][v]:
return False # Negative-weight cycle found
return True # No negative-weight cycle
if __name__ == "__main__":
graph = [
[0, -1, 4, 0, 0, 0],
[0, 0, 3, 2, 2, 0],
[0, 0, 0, 0, 0, 2],
[0, 1, 5, 0, 0, 0],
[0, 0, 0, -3, 0, 0],
[0, 0, 0, 0, 1, 0]
]
source = 0
distance = [0] * V
predecessor = [-1] * V
# Call the bellman_ford function
has_negative_cycle = bellman_ford(graph, source, distance, predecessor)
if not has_negative_cycle:
print("Graph contains negative-weight cycle.")
else:
print(f"Shortest distances from vertex {source}:")
for i in range(V):
print(f"Vertex {i}: Distance = {distance[i]}, Predecessor = {predecessor[i]}")
# Print the shortest distance from vertex 0 to vertex 5
destination = 5
print(f"Shortest distance from vertex {source} to vertex {destination}: {distance[destination]}")
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
