Karger’s Minimum Cut Algorithm

Considering the real-world applications like image segmentation where objects that are focused by the camera need to be removed from the image. Here, each pixel is considered as a node and the capacity between these pixels is reduced. The algorithm that is followed is the minimum cut algorithm.

Minimum Cut is the removal of minimum number of edges in a graph (directed or undirected) such that the graph is divided into multiple separate graphs or disjoint set of vertices.

Let us look at an example for a clearer understanding of disjoint sets achieved

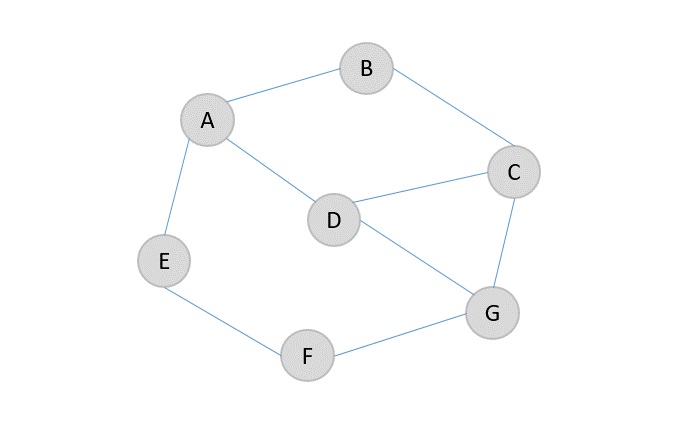
Edges {A, E} and {F, G} are the only ones loosely bonded to be removed easily from the graph. Hence, the minimum cut for the graph would be 2.

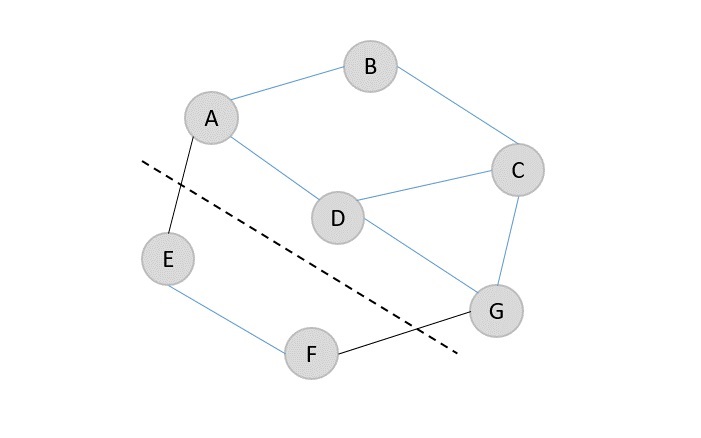
The resultant graphs after removing the edges A → E and F → G are {A, B, C, D, G} and {E, F}.

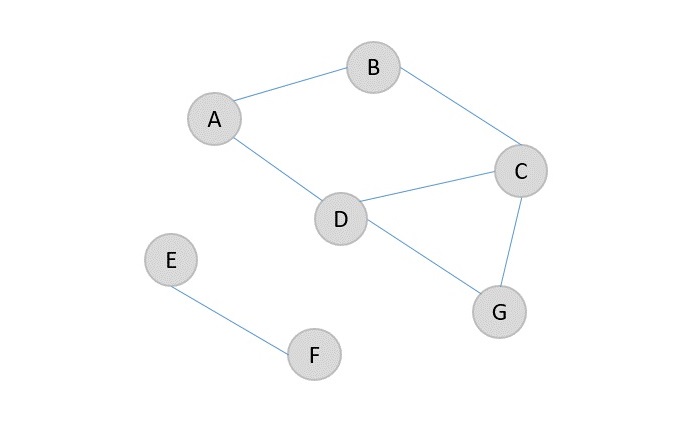
Karger’s Minimum Cut algorithm is a randomized algorithm to find the minimum cut of a graph. It uses the monte carlo approach so it is expected to run within a time constraint and have a minimal error in achieving output. However, if the algorithm is executed multiple times the probability of the error is reduced. The graph used in karger’s minimum cut algorithm is undirected graph with no weights.

Karger’s Minimum Cut Algorithm

The karger’s algorithm merges any two nodes in the graph into one node which is known as a supernode. The edge between the two nodes is contracted and the other edges connecting other adjacent vertices can be attached to the supernode.

Algorithm

Step 1 − Choose any random edge [u, v] from the graph G to be contracted.

Step 2 − Merge the vertices to form a supernode and connect the edges of the other adjacent nodes of the vertices to the supernode formed. Remove the self nodes, if any.

Step 3 − Repeat the process until there’s only two nodes left in the contracted graph.

Step 4 − The edges connecting these two nodes are the minimum cut edges.

The algorithm does not always the give the optimal output so the process is repeated multiple times to decrease the probability of error.

Pseudocode

Kargers_MinCut(edge, V, E):
   v = V
   while(v > 2):
      i=Random integer in the range [0, E-1]
      s1=find(edge[i].u)
      s2=find(edge[i].v)
      if(s1 != s2):
         v = v-1
         union(u, v)
   mincut=0
   for(i in the range 0 to E-1):
      s1=find(edge[i].u)
      s2=find(edge[i].v)
      if(s1 != s2):
         mincut = mincut + 1
   return mincut

Example

Applying the algorithm on an undirected unweighted graph G {V, E} where V and E are sets of vertices and edges present in the graph, let us find the minimum cut −

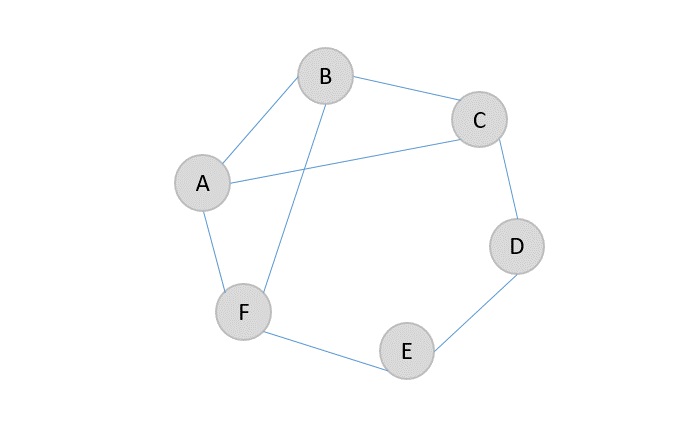
Step 1

Choose any edge, say A → B, and contract the edge by merging the two vertices into one supernode. Connect the adjacent vertex edges to the supernode. Remove the self loops, if any.

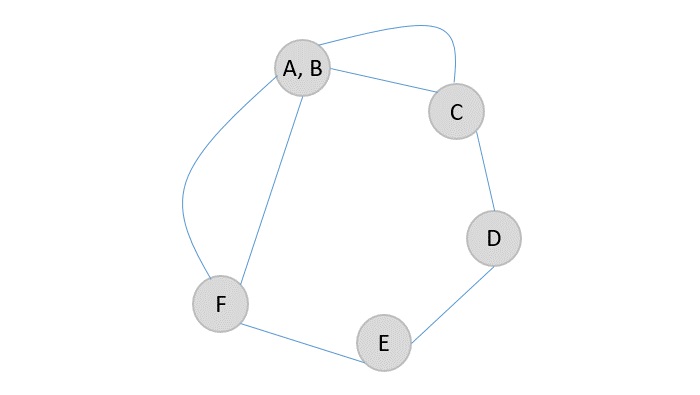
Step 2

Contract another edge (A, B) → C, so the supernode will become (A, B, C) and the adjacent edges are connected to the newly formed bigger supernode.

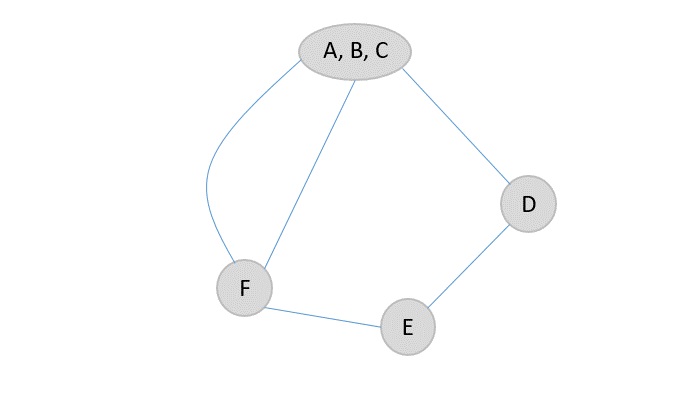
Step 3

The node D only has one edge connected to the supernode and one adjacent edge so it will be easier to contract and connect the adjacent edge to the new supernode formed.

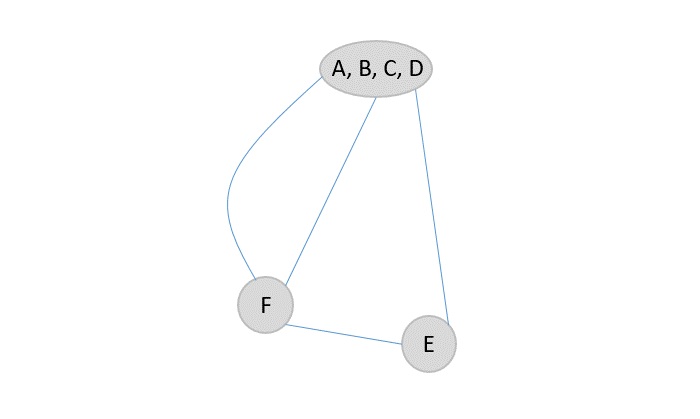
Step 4

Among F and E vertices, F is more strongly bonded to the supernode, so the edges connecting F and (A, B, C, D) are contracted.

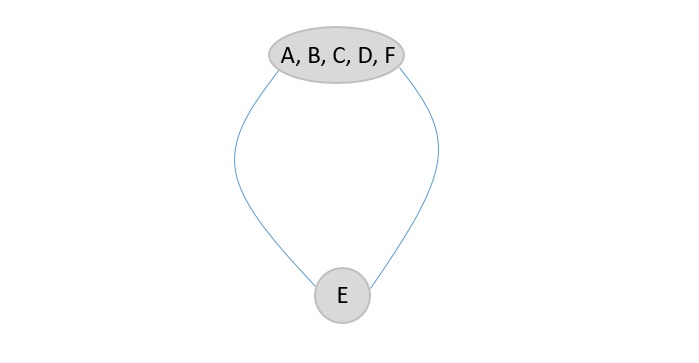
Step 5

Since there are only two nodes present in the graph, the number of edges are the final minimum cut of the graph. In this case, the minimum cut of given graph is 2.

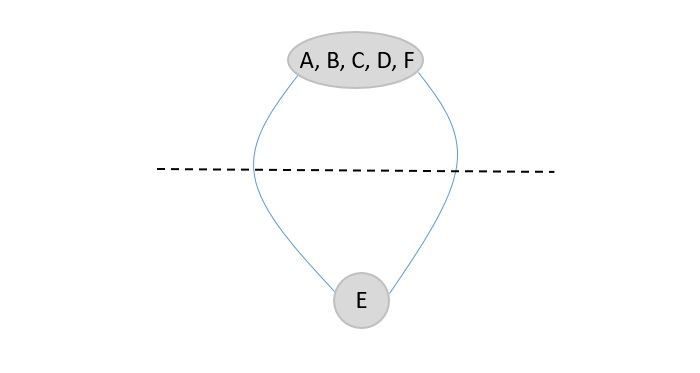
The minimum cut of the original graph is 2 (E → D and E → F).

Implementation

Following are the implementations of the above approach in various programming langauges −

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
struct Edge {
    int u, v;
};
struct Graph {
    int V;
    struct Edge* edges;
};
struct Graph* createGraph(int V, int E) {
    struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
    graph->V = V;
    graph->edges = (struct Edge*)malloc(E * sizeof(struct Edge));
    return graph;
}
int find(int parent[], int i) {
    if (parent[i] == i)
        return i;
    return find(parent, parent[i]);
}
void unionSets(int parent[], int rank[], int x, int y) {
    int xroot = find(parent, x);
    int yroot = find(parent, y);
    if (rank[xroot] < rank[yroot])
        parent[xroot] = yroot;
    else if (rank[xroot] > rank[yroot])
        parent[yroot] = xroot;
    else {
        parent[yroot] = xroot;
        rank[xroot]++;
    }
}
int kargerMinCut(struct Graph* graph) {
    int V = graph->V;
    int E = V * (V - 1) / 2;
    struct Edge* edges = graph->edges;

    int* parent = (int*)malloc(V * sizeof(int));
    int* rank = (int*)malloc(V * sizeof(int));
    for (int i = 0; i < V; i++) {
        parent[i] = i;
        rank[i] = 0;
    }
    int v = V;
    while (v > 2) {
        int randomIndex = rand() % E;
        int u = edges[randomIndex].u;
        int w = edges[randomIndex].v;
        int setU = find(parent, u);
        int setW = find(parent, w);
        if (setU != setW) {
            v--;
            unionSets(parent, rank, setU, setW);
        }
        edges[randomIndex] = edges[E - 1];
        E--;
    }
    int minCut = 0;
    for (int i = 0; i < E; i++) {
        int setU = find(parent, edges[i].u);
        int setW = find(parent, edges[i].v);
        if (setU != setW)
            minCut++;
    }
    free(parent);
    free(rank);
    return minCut;
}
int main() {
    int V = 4;
    int E = 5;
    struct Graph* graph = createGraph(V, E);
    graph->edges[0].u = 0;
    graph->edges[0].v = 1;
    graph->edges[1].u = 0;
    graph->edges[1].v = 2;
    graph->edges[2].u = 0;
    graph->edges[2].v = 3;
    graph->edges[3].u = 1;
    graph->edges[3].v = 3;
    graph->edges[4].u = 2;
    graph->edges[4].v = 3;
    srand(time(NULL));
    int minCut = kargerMinCut(graph);
    printf("Minimum Cut: %d\n", minCut);
    free(graph->edges);
    free(graph);
    return 0;
}

Minimum Cut: 2

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
struct Edge {
    int u, v;
};
class Graph
{
private:
    int V;
    vector<Edge> edges;
    int find(vector<int>& parent, int i)
    {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }
    void unionSets(vector<int>& parent, vector<int>& rank, int x, int y)
    {
        int xroot = find(parent, x);
        int yroot = find(parent, y);

        if (rank[xroot] < rank[yroot])
            parent[xroot] = yroot;
        else if (rank[xroot] > rank[yroot])
            parent[yroot] = xroot;
        else {
            parent[yroot] = xroot;
            rank[xroot]++;
        }
    }
public:
    Graph(int vertices) : V(vertices) {}
    void addEdge(int u, int v)
    {
        edges.push_back({u, v});
    }
    int kargerMinCut()
    {
        vector<int> parent(V);
        vector<int> rank(V);
        for (int i = 0; i < V; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
        int v = V;
        while (v < 2) {
            int randomIndex = rand() % edges.size();
            int u = edges[randomIndex].u;
            int w = edges[randomIndex].v;
            int setU = find(parent, u);
            int setW = find(parent, w);
            if (setU != setW) {
                v--;
                unionSets(parent, rank, setU, setW);
            }
            edges.erase(edges.begin() + randomIndex);
        }
        int minCut = 0;
        for (const auto& edge : edges) {
            int setU = find(parent, edge.u);
            int setW = find(parent, edge.v);
            if (setU != setW)
                minCut++;
        }
        return minCut;
    }
};
int main()
{
    // Create a graph
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(0, 3);
    g.addEdge(1, 3);
    g.addEdge(2, 3);
    // Set seed for random number generation
    srand(time(nullptr));
    // Find the minimum cut
    int minCut = g.kargerMinCut();
    cout << "Minimum Cut: " << minCut << endl;
    return 0;
}

Minimum Cut: 5

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
class Edge {
    int u;
    int v;
    public Edge(int u, int v) {
        this.u = u;
        this.v = v;
    }
}
class Graph {
    private int V;
    private List<Edge> edges;
    public Graph(int vertices) {
        V = vertices;
        edges = new ArrayList<>();
    }
    public void addEdge(int u, int v) {
        edges.add(new Edge(u, v));
    }
    private int find(int[] parent, int i) {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }
    private void union(int[] parent, int[] rank, int x, int y) {
        int xroot = find(parent, x);
        int yroot = find(parent, y);
        if (rank[xroot] < rank[yroot])
            parent[xroot] = yroot;
        else if (rank[xroot] > rank[yroot])
            parent[yroot] = xroot;
        else {
            parent[yroot] = xroot;
            rank[xroot]++;
        }
    }
    public int kargerMinCut() {
        int[] parent = new int[V];
        int[] rank = new int[V];
        for (int i = 0; i < V; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
        int v = V;
        while (v > 2) {
            Random rand = new Random();
            int randomIndex = rand.nextInt(edges.size());
            int u = edges.get(randomIndex).u;
            int w = edges.get(randomIndex).v;
            int setU = find(parent, u);
            int setW = find(parent, w);
            if (setU != setW) {
                v--;
                union(parent, rank, setU, setW);
            }
            edges.remove(randomIndex);
        }
        int minCut = 0;
        for (Edge edge : edges) {
            int setU = find(parent, edge.u);
            int setW = find(parent, edge.v);
            if (setU != setW)
                minCut++;
        }
        return minCut;
    }
}
public class Main {
    public static void main(String[] args) {
        // Create a graph
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(0, 3);
        g.addEdge(1, 3);
        g.addEdge(2, 3);
        // Set seed for random number generation
        Random rand = new Random();
        rand.setSeed(System.currentTimeMillis());
        // Find the minimum cut
        int minCut = g.kargerMinCut();
        System.out.println("Minimum Cut: " + minCut);
    }
}

Minimum Cut: 3

import random
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.edges = []
    def addEdge(self, u, v):
        self.edges.append((u, v))
    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])
    def union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1
    def kargerMinCut(self):
        parent = [i for i in range(self.V)]
        rank = [0] * self.V
        v = self.V
        while v > 2:
            i = random.randint(0, len(self.edges) - 1)
            u, w = self.edges[i]
            setU = self.find(parent, u)
            setW = self.find(parent, w)
            if setU != setW:
                v -= 1
                self.union(parent, rank, setU, setW)
            self.edges.pop(i)
        minCut = 0
        for u, w in self.edges:
            setU = self.find(parent, u)
            setW = self.find(parent, w)
            if setU != setW:
                minCut += 1
        return minCut
# Create a graph
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(0, 3)
g.addEdge(1, 3)
g.addEdge(2, 3)
# Set seed for random number generation
random.seed()
# Find the minimum cut
minCut = g.kargerMinCut()
print("Minimum Cut:", minCut)

Minimum Cut: 2