Kruskal’s Minimal Spanning Tree

Kruskal’s minimal spanning tree algorithm is one of the efficient methods to find the minimum spanning tree of a graph. A minimum spanning tree is a subgraph that connects all the vertices present in the main graph with the least possible edges and minimum cost (sum of the weights assigned to each edge).

The algorithm first starts from the forest – which is defined as a subgraph containing only vertices of the main graph – of the graph, adding the least cost edges later until the minimum spanning tree is created without forming cycles in the graph.

Kruskal’s algorithm has easier implementation than prim’s algorithm, but has higher complexity.

Kruskal’s Algorithm

The inputs taken by the kruskal’s algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S and the minimum spanning tree of graph G is obtained as an output.

Algorithm

• Sort all the edges in the graph in an ascending order and store it in an array edge[].

• Construct the forest of the graph on a plane with all the vertices in it.

• Select the least cost edge from the edge[] array and add it into the forest of the graph. Mark the vertices visited by adding them into the visited[] array.

• Repeat the steps 2 and 3 until all the vertices are visited without having any cycles forming in the graph

• When all the vertices are visited, the minimum spanning tree is formed.

• Calculate the minimum cost of the output spanning tree formed.

Examples

Construct a minimum spanning tree using kruskal’s algorithm for the graph given below −

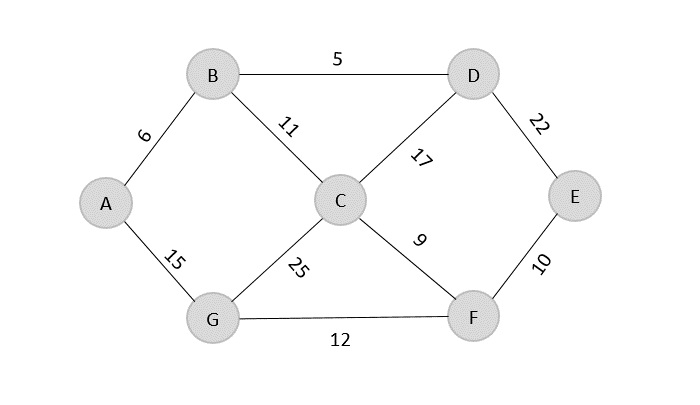
Solution

As the first step, sort all the edges in the given graph in an ascending order and store the values in an array.

Then, construct a forest of the given graph on a single plane.

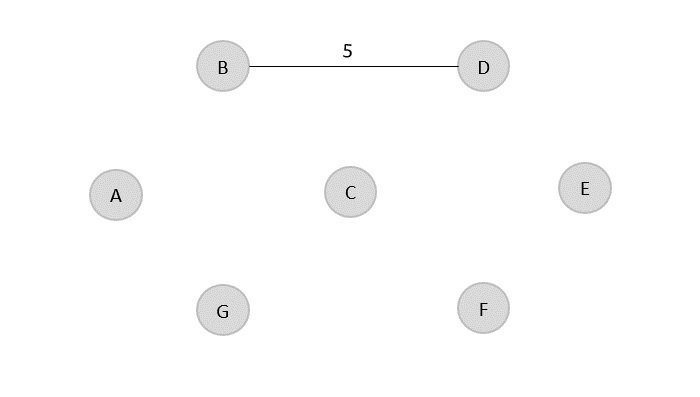
From the list of sorted edge costs, select the least cost edge and add it onto the forest in output graph.

B → D = 5
Minimum cost = 5
Visited array, v = {B, D}

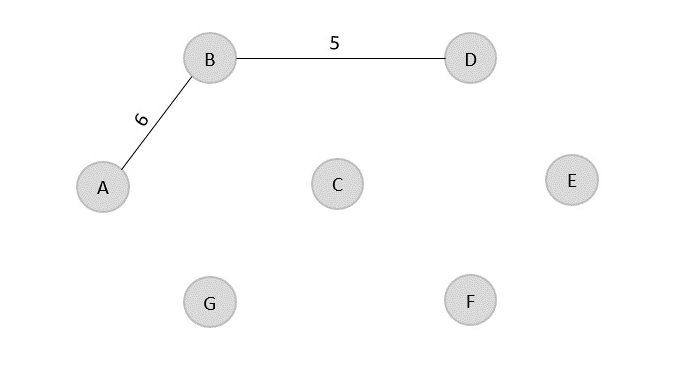
Similarly, the next least cost edge is B → A = 6; so we add it onto the output graph.

Minimum cost = 5 + 6 = 11
Visited array, v = {B, D, A}

The next least cost edge is C → F = 9; add it onto the output graph.

Minimum Cost = 5 + 6 + 9 = 20
Visited array, v = {B, D, A, C, F}

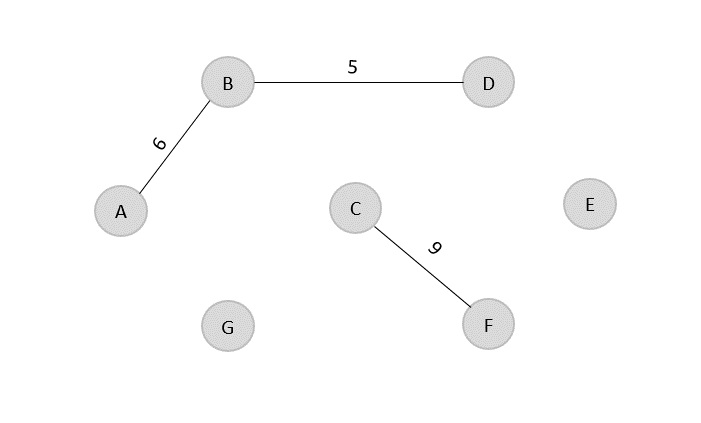
The next edge to be added onto the output graph is F → E = 10.

Minimum Cost = 5 + 6 + 9 + 10 = 30
Visited array, v = {B, D, A, C, F, E}

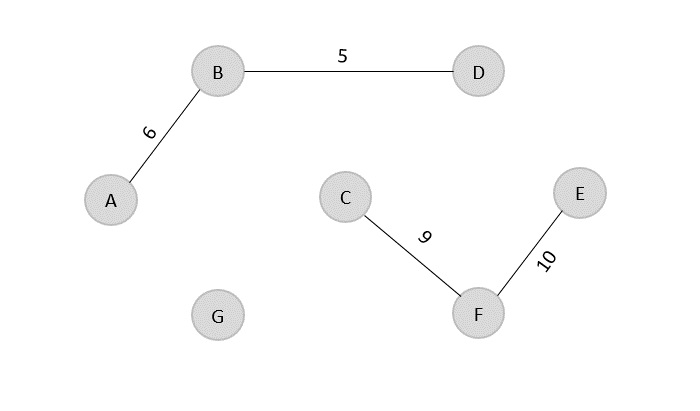
The next edge from the least cost array is B → C = 11, hence we add it in the output graph.

Minimum cost = 5 + 6 + 9 + 10 + 11 = 41
Visited array, v = {B, D, A, C, F, E}

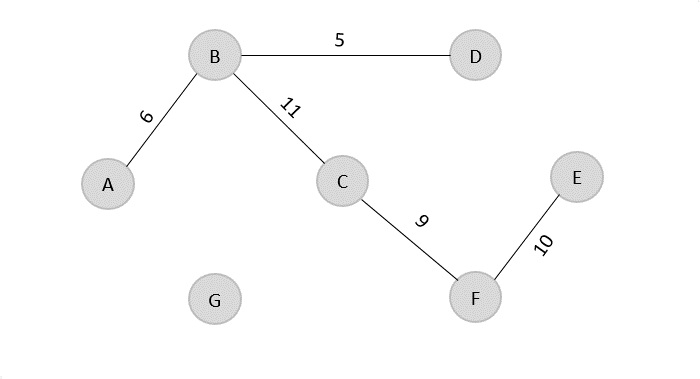
The last edge from the least cost array to be added in the output graph is F → G = 12.

Minimum cost = 5 + 6 + 9 + 10 + 11 + 12 = 53
Visited array, v = {B, D, A, C, F, E, G}

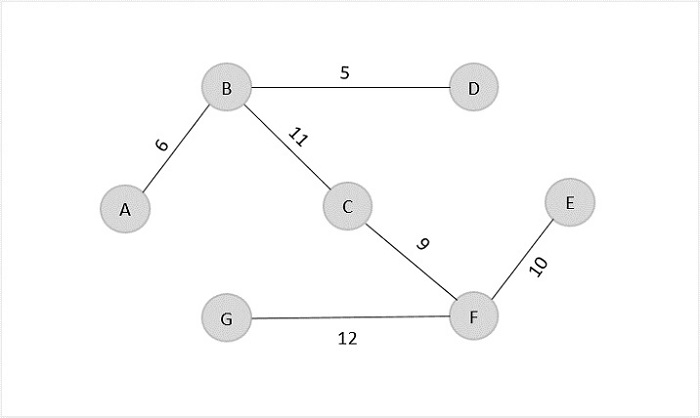
The obtained result is the minimum spanning tree of the given graph with cost = 53.

Example

The final program implements the Kruskal’s minimum spanning tree problem that takes the cost adjacency matrix as the input and prints the shortest path as the output along with the minimum cost.

#include <stdio.h>
#include <stdlib.h>
#define inf 999999
int i,j,k,a,b,u,v,n,ne=1;
int min,mincost=0,p[9];
int cost[9][9] = {
   {0, 10, 20},
   {12, 0, 15},
   {16, 18, 0}
};
int applyfind(int);
int applyunion(int,int);
int applyfind(int i){
   while(p[i])
      i=p[i];
   return i;
}
int applyunion(int i,int j){
   if(i!=j) {
      p[j]=i;
      return 1;
   }
   return 0;
}
int main(){
   n = 3;
   printf("Minimum Cost Spanning Tree: \n");
   while(ne < n) {
      min = inf;
      for(i=1; i<=n; i++) {
         for(j=1; j <= n; j++) {
            if(cost[i][j] < min) {
               min=cost[i][j];
               a=u=i;
               b=v=j;
            }
         }
      }
      u=applyfind(u);
      v=applyfind(v);
      if(applyunion(u,v)) {
         printf("%d -> %d\n",a,b);
         mincost +=min;
      }
      cost[a][b]=cost[b][a]=999;
   }
   printf("\n\tMinimum cost = %d\n",mincost);
   return 0;
}

Enter number of vertices: 3
Enter the cost matrix:
0 10 20
12 0 15
16 18 0
Minimum Cost Spanning Tree: 1 -> 2
2 -> 3

#include <iostream>
#define inf 999999
int i,j,k,a,b,u,v,n,ne=1;
int min,mincost=0,p[9];
int cost[9][9] = {
   {0, 10, 20},
   {12, 0, 15},
   {16, 18, 0}
};
int applyfind(int);
int applyunion(int,int);
int applyfind(int i){
   while(p[i])
      i=p[i];
   return i;
}
int applyunion(int i,int j){
   if(i!=j) {
      p[j]=i;
      return 1;
   }
   return 0;
}
int main(){
   n = 3;
   printf("Minimum Cost Spanning Tree: \n");
   while(ne < n) {
      min = inf;
      for(i=1; i<=n; i++) {
         for(j=1; j <= n; j++) {
            if(cost[i][j] < min) {
               min=cost[i][j];
               a=u=i;
               b=v=j;
            }
         }
      }
      u=applyfind(u);
      v=applyfind(v);
      if(applyunion(u,v)) {
         printf("%d -> %d\n",a,b);
         mincost +=min;
      }
      cost[a][b]=cost[b][a]=999;
   }
   printf("\n\tMinimum cost = %d\n",mincost);
   return 0;
}

Minimum Cost Spanning Tree: 
1 -> 3
2 -> 3

import java.util.*;
public class Main {
   static int k, a, b, u, v, n, ne=1, min, mincost=0;
   static int cost[][] = {{0, 10, 20},{12, 0, 15},{16, 18, 0}};
   static int p[] = new int[9];
   static int inf = 999999;
   static int applyfind(int i) {
      while(p[i] != 0)
      i=p[i];
      return i;
   }
   static int applyunion(int i,int j) {
      if(i!=j) {
         p[j]=i;
         return 1;
      }
      return 0;
   }
   public static void main(String args[]) {
      int i, j;
      n = 3;

      for(i=0; i<n; i++)
      for(j=0; j<n; j++) {
         if(cost[i][j]==0)
         cost[i][j]= inf;
      }
      System.out.println("Minimum Cost Spanning Tree: \n");
      while(ne < n) {
         min = inf;
         for(i=0; i<n; i++) {
            for(j=0; j<n; j++) {
               if(cost[i][j] < min) {
                  min=cost[i][j];
                  a=u=i;
                  b=v=j;
               }
            }
         }
         u=applyfind(u);
         v=applyfind(v);
         if(applyunion(u,v) != 0) {
            System.out.println(a + " -> " + b);
            mincost +=min;
         }
         cost[a][b]=cost[b][a]=999;
      }
      System.out.println("\n\tMinimum cost = \n" + mincost);
   }
}

Minimum Cost Spanning Tree: 

0 -> 1
1 -> 2
2 -> 0

Kickstart Your Career

Get certified by completing the course

Get Started