Design and Analysis Binary Heap

---

---

There are several types of heaps, however in this chapter, we are going to discuss binary heap. A binary heap is a data structure, which looks similar to a complete binary tree. Heap data structure obeys ordering properties discussed below. Generally, a Heap is represented by an array. In this chapter, we are representing a heap by H.

As the elements of a heap is stored in an array, considering the starting index as 1, the position of the parent node of i^th element can be found at ⌊ i/2 ⌋ . Left child and right child of i^th node is at position 2i and 2i + 1.

A binary heap can be classified further as either a max-heap or a min-heap based on the ordering property.

Max-Heap

In this heap, the key value of a node is greater than or equal to the key value of the highest child.

Hence, H[Parent(i)] ≥ H[i]

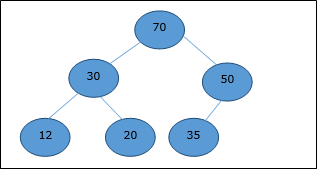
Min-Heap

In mean-heap, the key value of a node is lesser than or equal to the key value of the lowest child.

Hence, H[Parent(i)] ≤ H[i]

In this context, basic operations are shown below with respect to Max-Heap. Insertion and deletion of elements in and from heaps need rearrangement of elements. Hence, Heapify function needs to be called.

Array Representation

A complete binary tree can be represented by an array, storing its elements using level order traversal.

Let us consider a heap (as shown below) which will be represented by an array H.

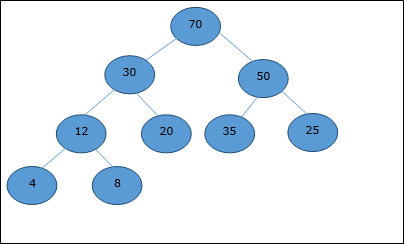
Considering the starting index as 0, using level order traversal, the elements are being kept in an array as follows.

Index	0	1	2	3	4	5	6	7	8	...
elements	70	30	50	12	20	35	25	4	8	...

In this context, operations on heap are being represented with respect to Max-Heap.

To find the index of the parent of an element at index i, the following algorithm Parent (numbers[], i) is used.

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

The index of the left child of an element at index i can be found using the following algorithm, Left-Child (numbers[], i).

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL 

The index of the right child of an element at index i can be found using the following algorithm, Right-Child(numbers[], i).

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL