Data Structures - Searching Algorithms

Table of content

In the previous section, we have discussed various Sorting Techniques and cases in which they can be used. However, the main idea behind performing sorting is to arrange the data in an orderly way, making it easier to search for any element within the sorted data.

Searching is a process of finding a particular record, which can be a single element or a small chunk, within a huge amount of data. The data can be in various forms: arrays, linked lists, trees, heaps, and graphs etc. With the increasing amount of data nowadays, there are multiple techniques to perform the searching operation.

Searching Algorithms in Data Structures

Various searching techniques can be applied on the data structures to retrieve certain data. A search operation is said to be successful only if it returns the desired element or data; otherwise, the searching method is unsuccessful.

There are two categories these searching techniques fall into. They are −

  • Sequential Searching

  • Interval Searching

Sequential Searching

As the name suggests, the sequential searching operation traverses through each element of the data sequentially to look for the desired data. The data need not be in a sorted manner for this type of search.

Example − Linear Search

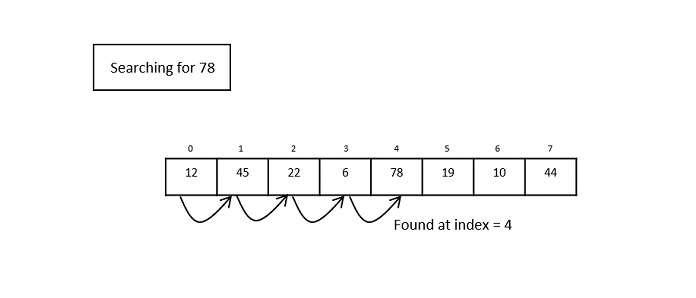
Linear_Search

Fig. 1: Linear Search Operation

Interval Searching

Unlike sequential searching, the interval searching operation requires the data to be in a sorted manner. This method usually searches the data in intervals; it could be done by either dividing the data into multiple sub-parts or jumping through the indices to search for an element.

Example − Binary Search, Jump Search etc.

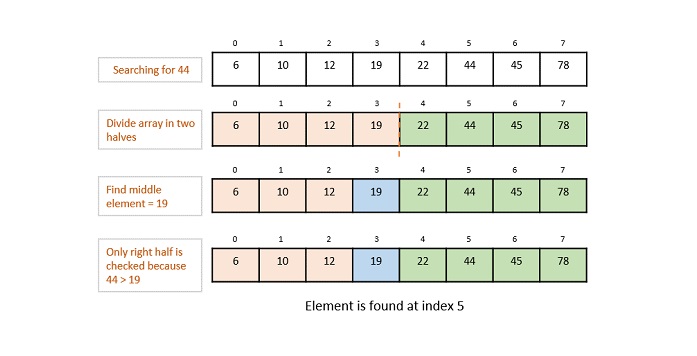
Binary_Search_Operation

Fig. 2: Binary Search Operation

Evaluating Searching Algorithms

Usually, not all searching techniques are suitable for all types of data structures. In some cases, a sequential search is preferable while in other cases interval searching is preferable. Evaluation of these searching techniques is done by checking the running time taken by each searching method on a particular input.

This is where asymptotic notations come into the picture. To learn more about Asymptotic Notations, please click here.

To explain briefly, there are three different cases of time complexity in which a program can run. They are −

  • Best Case

  • Average Case

  • Worst Case

We mostly concentrate on the only best-case and worst-case time complexities, as the average case is difficult to compute. And since the running time is based on the amount of input given to the program, the worst-case time complexity best describes the performance of any algorithm.

For instance, the best case time complexity of a linear search is O(1) where the desired element is found in the first iteration; whereas the worst case time complexity is O(n) when the program traverses through all the elements and still does not find an element. This is labelled as an unsuccessful search. Therefore, the actual time complexity of a linear search is seen as O(n), where n is the number of elements present in the input data structure.

Many types of searching methods are used to search for data entries in various data structures. Some of them include −

We will look at each of these searching methods elaborately in the following chapters.

Advertisements