Fibonacci Search Algorithm

As the name suggests, the Fibonacci Search Algorithm uses Fibonacci numbers to search for an element in a sorted input array.

But first, let us revise our knowledge on Fibonacci numbers −

Fibonacci Series is a series of numbers that have two primitive numbers 0 and 1. The successive numbers are the sum of preceding two numbers in the series. This is an infinite constant series, therefore, the numbers in it are fixed. The first few numbers in this Fibonacci series include −

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

The main idea behind the Fibonacci series is also to eliminate the least possible places where the element could be found. In a way, it acts like a divide & conquer algorithm (logic being the closest to binary search algorithm). This algorithm, like jump search and exponential search, also skips through the indices of the input array in order to perform searching.

Fibonacci Search Algorithm

The Fibonacci Search Algorithm makes use of the Fibonacci Series to diminish the range of an array on which the searching is set to be performed. With every iteration, the search range decreases making it easier to locate the element in the array. The detailed procedure of the searching is seen below −

Step 1 − As the first step, find the immediate Fibonacci number that is greater than or equal to the size of the input array. Then, also hold the two preceding numbers of the selected Fibonacci number, that is, we hold Fm, Fm-1, Fm-2 numbers from the Fibonacci Series.

Step 2 − Initialize the offset value as -1, as we are considering the entire array as the searching range in the beginning.

Step 3 − Until Fm-2 is greater than 0, we perform the following steps −

• Compare the key element to be found with the element at index [min(offset+F_m-2,n-1)]. If a match is found, return the index.

• If the key element is found to be lesser value than this element, we reduce the range of the input from 0 to the index of this element. The Fibonacci numbers are also updated with F_m = F_m-2.

• But if the key element is greater than the element at this index, we remove the elements before this element from the search range. The Fibonacci numbers are updated as F_m = F_m-1. The offset value is set to the index of this element.

Step 4 − As there are two 1s in the Fibonacci series, there arises a case where your two preceding numbers will become 1. So if F_m-1 becomes 1, there is only one element left in the array to be searched. We compare the key element with that element and return the 1st index. Otherwise, the algorithm returns an unsuccessful search.

Pseudocode

Begin Fibonacci Search
   n <- size of the input array
   offset = -1
   Fm2 := 0
   Fm1 := 1
   Fm := Fm2 + Fm1
   while Fm < n do:
      Fm2 = Fm1
      Fm1 = Fm
      Fm = Fm2 + Fm1
   done
   while fm > 1 do:
      i := minimum of (offset + fm2, n – 1)
      if (A[i] < x) then:
         Fm := Fm1
         Fm1 := Fm2
         Fm2 := Fm - Fm1
         offset = i
      end
      else if (A[i] > x) then:
         Fm = Fm2
         Fm1 = Fm1 - Fm2
         Fm2 = Fm - Fm1
      end
      else
         return i;
      end
   done
   if (Fm1 and Array[offset + 1] == x) then:
      return offset + 1
   end
   return invalid location;
end

Analysis

The Fibonacci Search algorithm takes logarithmic time complexity to search for an element. Since it is based on a divide on a conquer approach and is similar to idea of binary search, the time taken by this algorithm to be executed under the worst case consequences is O(log n).

Example

Suppose we have a sorted array of elements {12, 14, 16, 17, 20, 24, 31, 43, 50, 62} and need to identify the location of element 24 in it using Fibonacci Search.

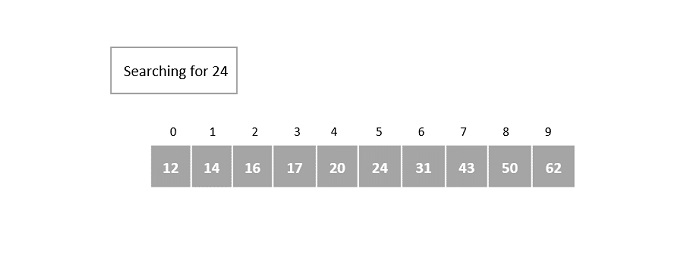
Step 1

The size of the input array is 10. The smallest Fibonacci number greater than 10 is 13.

Therefore, F_m = 13, F_m-1 = 8, F_m-2 = 5.

We initialize offset = -1

Step 2

In the first iteration, compare it with the element at index = minimum (offset + F_m-2, n – 1) = minimum (-1 + 5, 9) = minimum (4, 9) = 4.

The fourth element in the array is 20, which is not a match and is less than the key element.

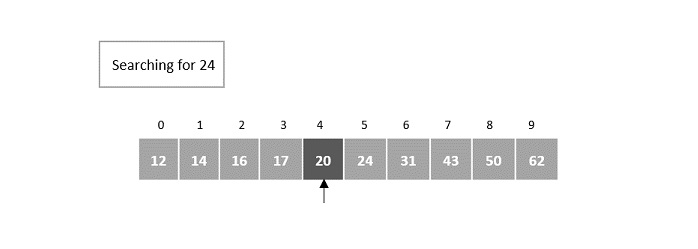
Step 3

In the second iteration, update the offset value and the Fibonacci numbers.

Since the key is greater, the offset value will become the index of the element, i.e. 4. Fibonacci numbers are updated as F_m = F_m-1 = 8.

Fm-1 = 5, Fm-2 = 3.

Now, compare it with the element at index = minimum (offset + F_m-2, n – 1) = minimum (4 + 3, 9) = minimum (7, 9) = 7.

Element at the 7^th index of the array is 43, which is not a match and is also lesser than the key.

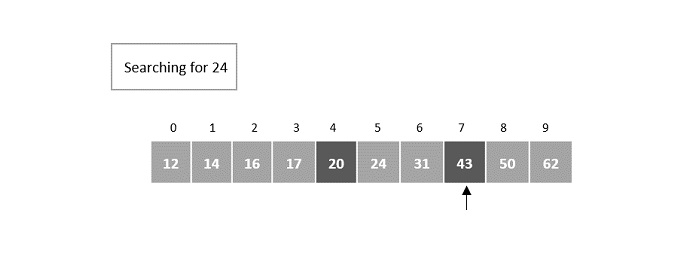
Step 4

We discard the elements after the 7th index, so n = 7 and offset value remains 4.

Fibonacci numbers are pushed two steps backward, i.e. F_m = F_m-2 = 3.

F_m-1 = 2, F_m-2 = 1.

Now, compare it with the element at index = minimum (offset + Fm-2, n – 1) = minimum (4 + 1, 6) = minimum (5, 7) = 5.

The element at index 5 in the array is 24, which is our key element. 5^th index is returned as the output for this example array.

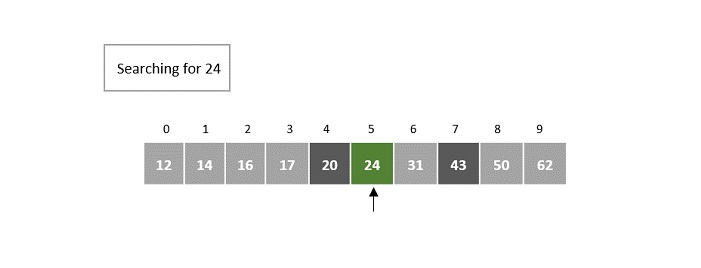
The output is returned as 5.

Implementation

The Fibonacci search algorithm uses the divide and conquer strategy to eliminate the search spaces that are not likely to contain the required element. This elimination is done with the help of the Fibonacci numbers to narrow down the search range within an input array. The implementation for the Fibonacci search method in four different programming languages is shown below −

#include <stdio.h>
int min(int, int);
int fibonacci_search(int[], int, int);
int min(int a, int b){
    return (a > b) ? b : a;
}
int fibonacci_search(int arr[], int n, int key){
    int offset = -1;
    int Fm2 = 0;
    int Fm1 = 1;
    int Fm = Fm2 + Fm1;
    while (Fm < n) {
        Fm2 = Fm1;
        Fm1 = Fm;
        Fm = Fm2 + Fm1;
    }
    while (Fm > 1) {
        int i = min(offset + Fm2, n - 1);
        if (arr[i] < key) {
            Fm = Fm1;
            Fm1 = Fm2;
            Fm2 = Fm - Fm1;
            offset = i;
        } else if (arr[i] > key) {
            Fm = Fm2;
            Fm1 = Fm1 - Fm2;
            Fm2 = Fm - Fm1;
        } else
            return i;
    }
    if (Fm1 && arr[offset + 1] == key)
        return offset + 1;
    return -1;
}
int main(){
   int i, n, key, pos;
   int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
   printf("Array elements are: ");
   int len = sizeof(arr) / sizeof(arr[0]);
   for(int j = 0; j<len; j++){
      printf("%d ", arr[j]);
   }
   n = 10;
   key = 67;
   printf("\nThe element to be searched: %d", key); 
   pos = fibonacci_search(arr, n, key);
    if(pos >= 0)
        printf("\nThe element is found at index %d", pos);
    else
        printf("\nUnsuccessful Search");
}

Array elements are: 6 11 19 24 33 54 67 81 94 99 
The element to be searched: 67
The element is found at index 6

#include <iostream>
using namespace std;
int min(int, int);
int fibonacci_search(int[], int, int);
int min(int a, int b){
   return (a > b) ? b : a;
}
int fibonacci_search(int arr[], int n, int key){
   int offset = -1;
   int Fm2 = 0;
   int Fm1 = 1;
   int Fm = Fm2 + Fm1;
   while (Fm < n) {
      Fm2 = Fm1;
      Fm1 = Fm;
      Fm = Fm2 + Fm1;
   }
   while (Fm > 1) {
      int i = min(offset + Fm2, n - 1);
      if (arr[i] < key) {
         Fm = Fm1;
         Fm1 = Fm2;
         Fm2 = Fm - Fm1;
         offset = i;
      } else if (arr[i] > key) {
         Fm = Fm2;
         Fm1 = Fm1 - Fm2;
         Fm2 = Fm - Fm1;
      } else
         return i;
   }
   if (Fm1 && arr[offset + 1] == key)
      return offset + 1;
   return -1;
}
int main(){
   int i, n, key, pos;
   int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
   cout<<"Array elements are: ";
   for(auto j : arr){
      cout<<j<<" ";
   }
   n = 10;
   key = 67;
   cout<<"\nThe element to be searched: "<<key;
   pos = fibonacci_search(arr, n, key);
   if(pos >= 0)
      cout << "\nThe element is found at index " << pos;
   else
      cout << "\nUnsuccessful Search";
}

Array elements are: 6 11 19 24 33 54 67 81 94 99 
The element to be searched: 67
The element is found at index 6

import java.io.*;
import java.util.Scanner;
public class FibonacciSearch {
   static int min(int a, int b) {
      return (a > b) ? b : a;
   }
   static int fibonacci_search(int arr[], int n, int key) {
      int offset = -1;
      int Fm2 = 0;
      int Fm1 = 1;
      int Fm = Fm2 + Fm1;
      while (Fm < n) {
         Fm2 = Fm1;
         Fm1 = Fm;
         Fm = Fm2 + Fm1;
      }
      while (Fm > 1) {
         int i = min(offset + Fm2, n - 1);
         if (arr[i] < key) {
            Fm = Fm1;
            Fm1 = Fm2;
            Fm2 = Fm - Fm1;
            offset = i;
        } else if (arr[i] > key) {
            Fm = Fm2;
            Fm1 = Fm1 - Fm2;
            Fm2 = Fm - Fm1;
        } else
          return i;
      }
      if (Fm1 == 1 && arr[offset + 1] == key)
         return offset + 1;
      return -1;
   }
   public static void main(String args[]) {
      int i, n, key;
      int arr[] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
	  System.out.print("Array elements are: ");
	  for(int j = 0; j<arr.length; j++){
	     System.out.print(arr[j] + " ");
      }
      n = 10;
      key = 67;
	  System.out.print("\nThe element to be searched: " + key);
      int pos = fibonacci_search(arr, n, key);
      if(pos >= 0)
         System.out.print("\nThe element is found at index " + pos);
      else
         System.out.print("\nUnsuccessful Search");
   }
}

Array elements are: 6 11 19 24 33 54 67 81 94 99 
The element to be searched: 67
The element is found at index 6

def fibonacci_search(arr, n, key):
   offset = -1
   Fm2 = 0
   Fm1 = 1
   Fm = Fm2 + Fm1
   while (Fm < n):
      Fm2 = Fm1
      Fm1 = Fm
      Fm = Fm2 + Fm1
   while (Fm > 1):
      i = min(offset + Fm2, n - 1)
      if (arr[i] < key):
         Fm = Fm1
         Fm1 = Fm2
         Fm2 = Fm - Fm1
         offset = i
      elif (arr[i] > key):
         Fm = Fm2
         Fm1 = Fm1 - Fm2
         Fm2 = Fm - Fm1
      else:
         return i
   if (Fm1 == 1 and arr[offset + 1] == key):
      return offset + 1
   return -1
arr = [12, 14, 16, 17, 20, 24, 31, 43, 50, 62]
print("Array elements are: ")
for j in range(len(arr)):
   print(arr[j], end = " ")
n = len(arr);
key = 20
print("\nThe element to be searched:", key)
index = fibonacci_search(arr, n, key)
if(index >= 0):
   print("The element is found at index: ", (index))
else:
   print("Unsuccessful Search")

Array elements are: 
12 14 16 17 20 24 31 43 50 62 
The element to be searched: 20
The element is found at index:  4