Karatsuba Algorithm

The Karatsuba algorithm is used by the system to perform fast multiplication on two n-digit numbers, i.e. the system compiler takes lesser time to compute the product than the time-taken by a normal multiplication.

The usual multiplication approach takes n² computations to achieve the final product, since the multiplication has to be performed between all digit combinations in both the numbers and then the sub-products are added to obtain the final product. This approach of multiplication is known as Naive Multiplication.

To understand this multiplication better, let us consider two 4-digit integers: 1456 and 6533, and find the product using Naive approach.

So, 1456 × 6533 =?

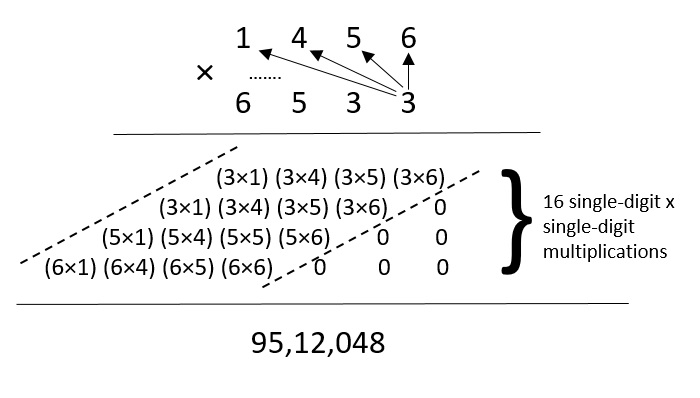
In this method of naive multiplication, given the number of digits in both numbers is 4, there are 16 single-digit × single-digit multiplications being performed. Thus, the time complexity of this approach is O(4²) since it takes 4² steps to calculate the final product.

But when the value of n keeps increasing, the time complexity of the problem also keeps increasing. Hence, Karatsuba algorithm is adopted to perform faster multiplications.

Karatsuba Algorithm

The main idea of the Karatsuba Algorithm is to reduce multiplication of multiple sub problems to multiplication of three sub problems. Arithmetic operations like additions and subtractions are performed for other computations.

For this algorithm, two n-digit numbers are taken as the input and the product of the two number is obtained as the output.

Step 1 − In this algorithm we assume that n is a power of 2.

Step 2 − If n = 1 then we use multiplication tables to find P = XY.

Step 3 − If n > 1, the n-digit numbers are split in half and represent the number using the formulae −

X = 10n/2X1 + X2
Y = 10n/2Y1 + Y2

where, X₁, X₂, Y₁, Y₂ each have n/2 digits.

Step 4 − Take a variable Z = W – (U + V),

where,

U = X1Y1, V = X2Y2
W = (X1 + X2) (Y1 + Y2), Z = X1Y2 + X2Y1.

Step 5 − Then, the product P is obtained after substituting the values in the formula −

P = 10n(U) + 10n/2(Z) + V
P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2.

Step 6 − Recursively call the algorithm by passing the sub problems (X₁, Y₁), (X₂, Y₂) and (X₁ + X₂, Y₁ + Y₂) separately. Store the returned values in variables U, V and W respectively.

Example

Let us solve the same problem given above using Karatsuba method, 1456 × 6533 −

The Karatsuba method takes the divide and conquer approach by dividing the problem into multiple sub-problems and applies recursion to make the multiplication simpler.

Step 1

Assuming that n is the power of 2, rewrite the n-digit numbers in the form of −

X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2

That gives us,

1456 = 102(14) + 56 
6533 = 102(65) + 33

First let us try simplifying the mathematical expression, we get,

(1400 × 6500) + (56 × 33) + (1400 × 33) + (6500 × 56) = 
104 (14 × 65) + 102 [(14 × 33) + (56 × 65)] + (33 × 56)

The above expression is the simplified version of the given multiplication problem, since multiplying two double-digit numbers can be easier to solve rather than multiplying two four-digit numbers.

However, that holds true for the human mind. But for the system compiler, the above expression still takes the same time complexity as the normal naive multiplication. Since it has 4 double-digit × double-digit multiplications, the time complexity taken would be −

14 × 65 → O(4)
14 × 33 → O(4)
65 × 56 → O(4)
56 × 33 → O(4)
= O (16)

Thus, the calculation needs to be simplified further.

Step 2

X = 1456 
Y = 6533

Since n is not equal to 1, the algorithm jumps to step 3.

X = 10n/2X1 + X2 
Y = 10n/2Y1 + Y2

That gives us,

1456 = 102(14) + 56 
6533 = 102(65) + 33

Calculate Z = W – (U + V) −

Z = (X1 + X2) (Y1 + Y2) – (X1Y1 + X2Y2) 
Z = X1Y2 + X2Y1 
Z = (14 × 33) + (65 × 56)

The final product,

P = 10n. U + 10n/2. Z + V 
   = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 
   = 104 (14 × 65) + 102 [(14 × 33) + (65 × 56)] + (56 × 33)

The sub-problems can be further divided into smaller problems; therefore, the algorithm is again called recursively.

Step 3

X₁ and Y₁ are passed as parameters X and Y.

So now, X = 14, Y = 65

X = 10n/2X1 + X2 
Y = 10n/2Y1 + Y2 
14 = 10(1) + 4 
65 = 10(6) + 5

Calculate Z = W – (U + V) −

Z = (X1 + X2) (Y1 + Y2) – (X1Y1 + X2Y2) 
Z = X1Y2 + X2Y1 
Z = (1 × 5) + (6 × 4) = 29 

P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 
   = 102 (1 × 6) + 101 (29) + (4 × 5) 
   = 910

Step 4

X₂ and Y₂ are passed as parameters X and Y.

So now, X = 56, Y = 33

X = 10n/2X1 + X2 
Y = 10n/2Y1 + Y2 
56 = 10(5) + 6 
33 = 10(3) + 3

Calculate Z = W – (U + V) −

Z = (X1 + X2) (Y1 + Y2) – (X1Y1 + X2Y2) 
Z = X1Y2 + X2Y1 
Z = (5 × 3) + (6 × 3) = 33 

P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 
= 102 (5 × 3) + 101 (33) + (6 × 3) 
= 1848

Step 5

X₁ + X₂ and Y₁ + Y₂ are passed as parameters X and Y.

So now, X = 70, Y = 98

X = 10n/2X1 + X2 
Y = 10n/2Y1 + Y2 
70 = 10(7) + 0 
98 = 10(9) + 8

Calculate Z = W – (U + V) −

Z = (X1 + X2) (Y1 + Y2) – (X1Y1 + X2Y2) 
Z = X1Y2 + X2Y1 
Z = (7 × 8) + (0 × 9) = 56 

P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 
= 102 (7 × 9) + 101 (56) + (0 × 8) 
=

Step 6

The final product,

P = 10n. U + 10n/2. Z + V

U = 910 
V = 1848 
Z = W – (U + V) = 6860 – (1848 + 910) = 4102

Substituting the values in equation,

P = 10n. U + 10n/2. Z + V 
P = 104 (910) + 102 (4102) + 1848 
P = 91,00,000 + 4,10,200 + 1848 
P = 95,12,048

Analysis

The Karatsuba algorithm is a recursive algorithm; since it calls smaller instances of itself during execution.

According to the algorithm, it calls itself only thrice on n/2-digit numbers in order to achieve the final product of two n-digit numbers.

Now, if T(n) represents the number of digit multiplications required while performing the multiplication,

T(n) = 3T(n/2)

This equation is a simple recurrence relation which can be solved as −

Apply T(n/2) = 3T(n/4) in the above equation, we get:
T(n) = 9T(n/4)
T(n) = 27T(n/8)
T(n) = 81T(n/16)
.
.
.
.
T(n) = 3i T(n/2i) is the general form of the recurrence relation 
of Karatsuba algorithm.

Recurrence relations can be solved using the master’s theorem, since we have a dividing function in the form of −

T(n) = aT(n/b) + f(n), where, a = 3, b = 2 and f(n) = 0 
which leads to k = 0.

Since f(n) represents work done outside the recursion, which are addition and subtraction arithmetic operations in Karatsuba, these arithmetic operations do not contribute to time complexity.

Check the relation between ‘a’ and ‘b^k’.

a > bk = 3 > 20

According to master’s theorem, apply case 1.

T(n) = O(nlogb a)
T(n) = O(nlog 3)

The time complexity of Karatsuba algorithm for fast multiplication is O(n^{log 3}).

Example

In the complete implementation of Karatsuba Algorithm, we are trying to multiply two higher-valued numbers. Here, since the long data type accepts decimals upto 18 places, we take the inputs as long values. The Karatsuba function is called recursively until the final product is obtained.

#include <stdio.h>
#include <math.h>
int get_size(long);
long karatsuba(long X, long Y){
   
   // Base Case
   if (X < 10 && Y < 10)
      return X * Y;
   
   // determine the size of X and Y
   int size = fmax(get_size(X), get_size(Y));
   if(size < 10)
      return X * Y;
   
   // rounding up the max length
   size = (size/2) + (size%2);
   long multiplier = pow(10, size);
   long b = X/multiplier;
   long a = X - (b * multiplier);
   long d = Y / multiplier;
   long c = Y - (d * size);
   long u = karatsuba(a, c);
   long z = karatsuba(a + b, c + d);
   long v = karatsuba(b, d);
   return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
   int count = 0;
   while (value > 0) {
      count++;
      value /= 10;
   }
   return count;
}
int main(){

   // two numbers
   long x = 145623;
   long y = 653324;
   printf("The final product is: %ld\n", karatsuba(x, y));
   return 0;
}

The final product is: 95139000852

#include <iostream>
#include <cmath>
using namespace std;
int get_size(long);
long karatsuba(long X, long Y){

   // Base Case
   if (X < 10 && Y < 10)
      return X * Y;

   // determine the size of X and Y
   int size = fmax(get_size(X), get_size(Y));
   if(size < 10)
      return X * Y;

   // rounding up the max length
   size = (size/2) + (size%2);
   long multiplier = pow(10, size);
   long b = X/multiplier;
   long a = X - (b * multiplier);
   long d = Y / multiplier;
   long c = Y - (d * size);
   long u = karatsuba(a, c);
   long z = karatsuba(a + b, c + d);
   long v = karatsuba(b, d);
   return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
   int count = 0;
   while (value > 0) {
      count++;
      value /= 10;
   }
   return count;
}
int main(){

   // two numbers
   long x = 145623;
   long y = 653324;
   cout << "The final product is: " << karatsuba(x, y) << endl;
   return 0;
}

The final product is: 95139000852

import java.io.*;
public class Main {
   static long karatsuba(long X, long Y) {
      // Base Case
      if (X < 10 && Y < 10)
         return X * Y;
      // determine the size of X and Y
      int size = Math.max(get_size(X), get_size(Y));
      if(size < 10)
         return X * Y;
      // rounding up the max length
      size = (size/2) + (size%2);
      long multiplier = (long)Math.pow(10, size);
      long b = X/multiplier;
      long a = X - (b * multiplier);
      long d = Y / multiplier;
      long c = Y - (d * size);
      long u = karatsuba(a, c);
      long z = karatsuba(a + b, c + d);
      long v = karatsuba(b, d);
      return u + ((z - u - v) * multiplier) + (v * (long)(Math.pow(10, 2 * size)));
   }
   static int get_size(long value) {
      int count = 0;
      while (value > 0) {
         count++;
         value /= 10;
      }
      return count;
   }
   public static void main(String args[]) {
      // two numbers
      long x = 145623;
      long y = 653324;
      System.out.print("The final product is: ");
      long product = karatsuba(x, y);
      System.out.println(product);
   }
}

The final product is: 95139000852

import math
def karatsuba(X, Y):
    if X < 10 and Y < 10:
        return X * Y
    size = max(get_size(X), get_size(Y))
    if size < 10:
        return X * Y
    size = (size // 2) + (size % 2)
    multiplier = 10 ** size
    b = X // multiplier
    a = X - (b * multiplier)
    d = Y // multiplier
    c = Y - (d * size)
    u = karatsuba(a, c)
    z = karatsuba(a + b, c + d)
    v = karatsuba(b, d)
    return u + ((z - u - v) * multiplier) + (v * (10 ** (2 * size)))
def get_size(value):
    count = 0
    while value > 0:
        count += 1
        value //= 10
    return count
x = 145623
y = 653324
print("The final product is: ", end="")
product = karatsuba(x, y)
print(product)

The final product is: 95139000852