Bucket Sort Algorithm

The Bucket Sort algorithm is similar to the Counting Sort algorithm, as it is just the generalized form of the counting sort. Bucket sort assumes that the input elements are drawn from a uniform distribution over the interval [0, 1).

Hence, the bucket sort algorithm divides the interval [0, 1) into ‘n’ equal parts, and the input elements are added to indexed buckets where the indices based on the lower bound of the (n × element) value. Since the algorithm assumes the values as the independent numbers evenly distributed over a small range, not many elements fall into one bucket only.

For example, let us look at an input list of elements, 0.08, 0.01, 0.19, 0.89, 0.34, 0.07, 0.30, 0.82, 0.39, 0.45, 0.36. The bucket sort would look like −

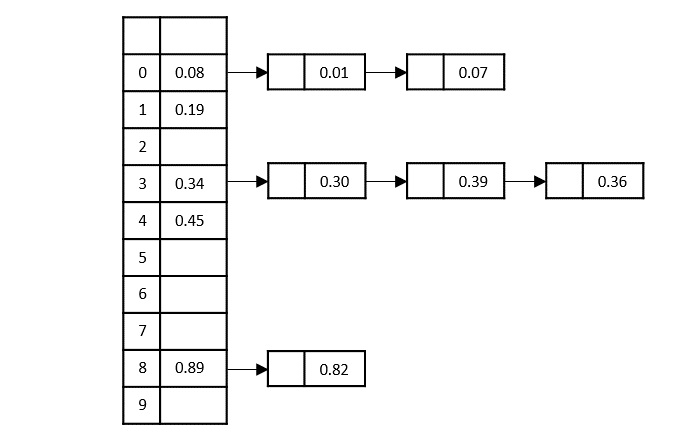
Bucket Sort Algorithm

Let us look at how this algorithm would proceed further below −

Step 1 − Divide the interval in ‘n’ equal parts, each part being referred to as a bucket. Say if n is 10, then there are 10 buckets; otherwise more.

Step 2 − Take the input elements from the input array A and add them to these output buckets B based on the computation formula, B[i]= $\lfloor$n.A[i]$\rfloor$

Step 3 − If there are any elements being added to the already occupied buckets, created a linked list through the corresponding bucket.

Step 4 − Then we apply insertion sort to sort all the elements in each bucket.

Step 5 − These buckets are concatenated together which in turn is obtained as the output.

Pseudocode

BUCKET-SORT(A)
let B[0 … n – 1] be a new array
n = A.length
for i = 0 to n – 1
   make B[i] an empty list
for i = 1 to n
   insert A[i] into list B[$\lfloor$𝑛.𝐴[𝑖]$\rfloor$]
for i = 0 to n – 1
   sort list B[i] with insertion sort
concatenate the lists B[0], B[1]; ………… ; B[n – 1] together in order

Analysis

The bucket sort algorithm assumes the identity of the input, therefore, the average case time complexity of the algorithm is Θ(n)

Example

Consider, an input list of elements, 0.78, 0.17, 0.93, 0.39, 0.26, 0.72, 0.21, 0.12, 0.33, 0.28, to sort these elements using bucket sort −

Solution

Step 1

Linearly insert all the elements from the index ‘0’ of the input array. That is, we insert 0.78 first followed by other elements sequentially. The position to insert the element is obtained using the formula − B[i]= $\lfloor$n.A[i]$\rfloor$, i.e, $\lfloor$10 ×0.78$\rfloor$=7

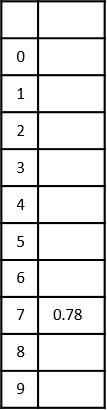
Now, we insert 0.17 at index $\lfloor$10 ×0.17$\rfloor$=1

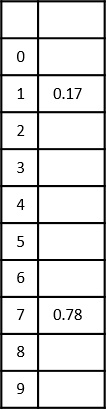
Step 3

Inserting the next element, 0.93 into the output buckets at $\lfloor$10 ×0.93$\rfloor$=9

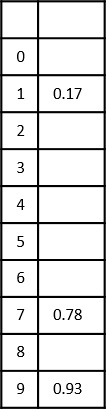
Step 4

Insert 0.39 at index 3 using the formula $\lfloor$10 ×0.39$\rfloor$=3

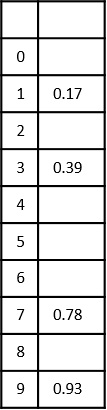
Step 5

Inserting the next element in the input array, 0.26, at position $\lfloor$10 ×0.26$\rfloor$=2

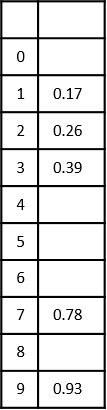
Step 6

Here is where it gets tricky. Now, the next element in the input list is 0.72 which needs to be inserted at index ‘7’ using the formula $\lfloor$10 ×0.72$\rfloor$=7. But there’s already a number in the 7^th bucket. So, a link is created from the 7^th index to store the new number like a linked list, as shown below −

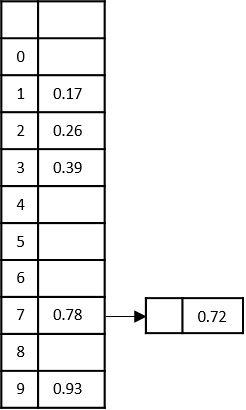
Step 7

Add the remaining numbers to the buckets in the similar manner by creating linked lists from the desired buckets. But while inserting these elements as lists, we apply insertion sort, i.e., compare the two elements and add the minimum value at the front as shown below −

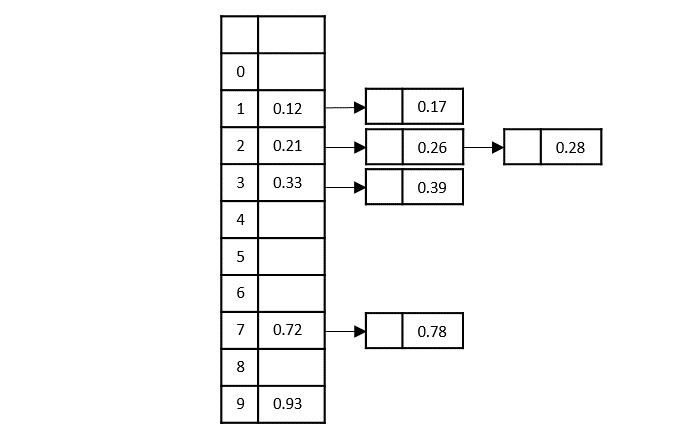
Step 8

Now, to achieve the output, concatenate all the buckets together.

0.12, 0.17, 0.21, 0.26, 0.28, 0.33, 0.39, 0.72, 0.78, 0.93

Implementation

The implementation of the bucket sort algorithm first retrieves the maximum element of the array and decides the bucket size of the output. The elements are inserted into these buckets based on few computations.

In this tutorial, we execute bucket sort in four programming languages.

#include <stdio.h>
void bucketsort(int a[], int n){ // function to implement bucket sort
   int max = a[0]; // get the maximum element in the array
   for (int i = 1; i < n; i++)
      if (a[i] > max)
         max = a[i];
   int b[max], i;
   for (int i = 0; i <= max; i++) {
      b[i] = 0;
   }
   for (int i = 0; i < n; i++) {
      b[a[i]]++;
   }
   for (int i = 0, j = 0; i <= max; i++) {
      while (b[i] > 0) {
         a[j++] = i;
         b[i]--;
      }
   }
}
int main(){
   int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
   int n = sizeof(a) / sizeof(a[0]); // n is the size of array
   printf("Before sorting array elements are: \n");
   for (int i = 0; i < n; ++i)
      printf("%d ", a[i]);
   bucketsort(a, n);
   printf("\nAfter sorting array elements are: \n");
   for (int i = 0; i < n; ++i)
      printf("%d ", a[i]);
}

Before sorting array elements are: 
12 45 33 87 56 9 11 7 67 
After sorting array elements are: 
7 9 11 12 33 45 56 67 87

#include <iostream>
using namespace std;
void bucketsort(int a[], int n){ // function to implement bucket sort
   int max = a[0]; // get the maximum element in the array
   for (int i = 1; i < n; i++)
      if (a[i] > max)
         max = a[i];
   int b[max], i;
   for (int i = 0; i <= max; i++) {
      b[i] = 0;
   }
   for (int i = 0; i < n; i++) {
      b[a[i]]++;
   }
   for (int i = 0, j = 0; i <= max; i++) {
      while (b[i] > 0) {
         a[j++] = i;
         b[i]--;
      }
   }
}
int main(){
   int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
   int n = sizeof(a) / sizeof(a[0]); // n is the size of array
   cout << "Before sorting array elements are: \n";
   for (int i = 0; i < n; ++i)
      cout << a[i] << " ";
   bucketsort(a, n);
   cout << "\nAfter sorting array elements are: \n";
   for (int i = 0; i < n; ++i)
      cout << a[i] << " ";
}

Before sorting array elements are: 
12 45 33 87 56 9 11 7 67 
After sorting array elements are: 
7 9 11 12 33 45 56 67 87

import java.io.*;
import java.util.*;
public class BucketSort {
   static void bucketsort(int a[], int n) { // function to implement bucket sort
      int max = a[0]; // get the maximum element in the array
      for (int i = 1; i < n; i++)
         if (a[i] > max)
            max = a[i];
      int b[] = new int[max+1];
      for (int i = 0; i <= max; i++) {
         b[i] = 0;
      }
      for (int i = 0; i < n; i++) {
         b[a[i]]++;
      }
      for (int i = 0, j = 0; i <= max; i++) {
         while (b[i] > 0) {
            a[j++] = i;
            b[i]--;
         }
      }
   }
   public static void main(String args[]) {
      int n = 9;
      int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
      System.out.println("Before sorting array elements are: ");
      for (int i = 0; i < n; ++i)
         System.out.print(a[i] + " ");
      bucketsort(a, n);
      System.out.println("\nAfter sorting array elements are: ");
      for (int i = 0; i < n; ++i)
         System.out.print(a[i] + " ");
   }
}

Before sorting array elements are: 
12 45 33 87 56 9 11 7 67 
After sorting array elements are: 
7 9 11 12 33 45 56 67 87 

def bucketsort(a, n):
    max_val = max(a)
    b = [0] * (max_val + 1)
    for i in range(n):
        b[a[i]] += 1
    j = 0
    for i in range(max_val + 1):
        while b[i] > 0:
            a[j] = i
            j += 1
            b[i] -= 1
a = [12, 45, 33, 87, 56, 9, 11, 7, 67]
n = len(a)
print("Before sorting array elements are: ")
print(a)
bucketsort(a, n)
print("\nAfter sorting array elements are: ")
print(a)

Before sorting array elements are: 
[12, 45, 33, 87, 56, 9, 11, 7, 67]

After sorting array elements are: 
[7, 9, 11, 12, 33, 45, 56, 67, 87]