Optimal Merge Pattern Algorithm

Merge a set of sorted files of different length into a single sorted file. We need to find an optimal solution, where the resultant file will be generated in minimum time.

If the number of sorted files are given, there are many ways to merge them into a single sorted file. This merge can be performed pair wise. Hence, this type of merging is called as 2-way merge patterns.

As, different pairings require different amounts of time, in this strategy we want to determine an optimal way of merging many files together. At each step, two shortest sequences are merged.

To merge a p-record file and a q-record file requires possibly p + q record moves, the obvious choice being, merge the two smallest files together at each step.

Two-way merge patterns can be represented by binary merge trees. Let us consider a set of n sorted files {f₁, f₂, f₃, …, f_n}. Initially, each element of this is considered as a single node binary tree. To find this optimal solution, the following algorithm is used.

Pseudocode

Following is the pseudocode of the Optimal Merge Pattern Algorithm −

 for i := 1 to n – 1 do  
   declare new node  
   node.leftchild := least (list) 
   node.rightchild := least (list) 
   node.weight) := ((node.leftchild).weight)+
   ((node.rightchild).weight)  
   insert (list, node);  
return least (list); 

At the end of this algorithm, the weight of the root node represents the optimal cost.

Examples

Let us consider the given files, f₁, f₂, f₃, f₄ and f₅ with 20, 30, 10, 5 and 30 number of elements respectively.

If merge operations are performed according to the provided sequence, then

M₁ = merge f₁ and f₂ => 20 + 30 = 50

M₂ = merge M₁ and f₃ => 50 + 10 = 60

M₃ = merge M₂ and f₄ => 60 + 5 = 65

M₄ = merge M₃ and f₅ => 65 + 30 = 95

Hence, the total number of operations is

50 + 60 + 65 + 95 = 270

Now, the question arises is there any better solution?

Sorting the numbers according to their size in an ascending order, we get the following sequence −

f₄, f₃, f₁, f₂, f₅

Hence, merge operations can be performed on this sequence

M₁ = merge f₄ and f₃ => 5 + 10 = 15

M₂ = merge M₁ and f₁ => 15 + 20 = 35

M₃ = merge M₂ and f₂ => 35 + 30 = 65

M₄ = merge M₃ and f₅ => 65 + 30 = 95

Therefore, the total number of operations is

15 + 35 + 65 + 95 = 210

Obviously, this is better than the previous one.

In this context, we are now going to solve the problem using this algorithm.

Initial Set

Step 1

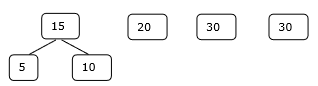
Step 2

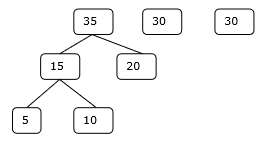
Step 3

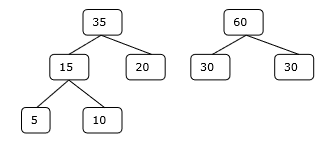
Step 4

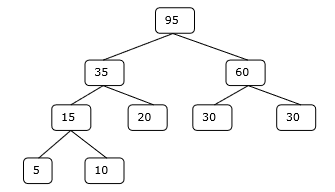
Hence, the solution takes 15 + 35 + 60 + 95 = 205 number of comparisons.

Example

Following are the implementations of the above approach in various programming languages −

#include <stdio.h>
#include <stdlib.h>
int optimalMerge(int files[], int n)
{
    // Sort the files in ascending order
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (files[j] > files[j + 1]) {
                int temp = files[j];
                files[j] = files[j + 1];
                files[j + 1] = temp;
            }
        }
    }
    int cost = 0;
    while (n > 1) {
        // Merge the smallest two files
        int mergedFileSize = files[0] + files[1];
        cost += mergedFileSize;
        // Replace the first file with the merged file size
        files[0] = mergedFileSize;
        // Shift the remaining files to the left
        for (int i = 1; i < n - 1; i++) {
            files[i] = files[i + 1];
        }
        n--; // Reduce the number of files
        // Sort the files again
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (files[j] > files[j + 1]) {
                    int temp = files[j];
                    files[j] = files[j + 1];
                    files[j + 1] = temp;
                }
            }
        }
    }
    return cost;
}
int main()
{
    int files[] = {5, 10, 20, 30, 30};
    int n = sizeof(files) / sizeof(files[0]);
    int minCost = optimalMerge(files, n);
    printf("Minimum cost of merging is: %d Comparisons\n", minCost);
    return 0;
}

Minimum cost of merging is: 205 Comparisons

#include <iostream>
#include <algorithm>
int optimalMerge(int files[], int n) {
    // Sort the files in ascending order
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (files[j] > files[j + 1]) {
                std::swap(files[j], files[j + 1]);
            }
        }
    }
    int cost = 0;
    while (n > 1) {
        // Merge the smallest two files
        int mergedFileSize = files[0] + files[1];
        cost += mergedFileSize;
        // Replace the first file with the merged file size
        files[0] = mergedFileSize;
        // Shift the remaining files to the left
        for (int i = 1; i < n - 1; i++) {
            files[i] = files[i + 1];
        }
        n--; // Reduce the number of files
        // Sort the files again
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (files[j] > files[j + 1]) {
                    std::swap(files[j], files[j + 1]);
                }
            }
        }
    }
    return cost;
}
int main() {
    int files[] = {5, 10, 20, 30, 30};
    int n = sizeof(files) / sizeof(files[0]);
    int minCost = optimalMerge(files, n);
    std::cout << "Minimum cost of merging is: " << minCost << " Comparisons\n";
    return 0;
}

Minimum cost of merging is: 205 Comparisons

import java.util.Arrays;
public class Main {
    public static int optimalMerge(int[] files, int n) {
        // Sort the files in ascending order
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (files[j] > files[j + 1]) {
                    // Swap files[j] and files[j + 1]
                    int temp = files[j];
                    files[j] = files[j + 1];
                    files[j + 1] = temp;
                }
            }
        }
        int cost = 0;
        while (n > 1) {
            // Merge the smallest two files
            int mergedFileSize = files[0] + files[1];
            cost += mergedFileSize;
            // Replace the first file with the merged file size
            files[0] = mergedFileSize;
            // Shift the remaining files to the left
            for (int i = 1; i < n - 1; i++) {
                files[i] = files[i + 1];
            }
            n--; // Reduce the number of files
            // Sort the files again
            for (int i = 0; i < n - 1; i++) {
                for (int j = 0; j < n - i - 1; j++) {
                    if (files[j] > files[j + 1]) {
                        // Swap files[j] and files[j + 1]
                        int temp = files[j];
                        files[j] = files[j + 1];
                        files[j + 1] = temp;
                    }
                }
            }
        }
        return cost;
    }
    public static void main(String[] args) {
        int[] files = {5, 10, 20, 30, 30};
        int n = files.length;
        int minCost = optimalMerge(files, n);
        System.out.println("Minimum cost of merging is: " + minCost + " Comparisons");
    }
}

Minimum cost of merging is: 205 Comparison

def optimal_merge(files):
    # Sort the files in ascending order
    files.sort()
    cost = 0
    while len(files) > 1:
        # Merge the smallest two files
        merged_file_size = files[0] + files[1]
        cost += merged_file_size
        # Replace the first file with the merged file size
        files[0] = merged_file_size
        # Remove the second file
        files.pop(1)
        # Sort the files again
        files.sort()
    return cost
files = [5, 10, 20, 30, 30]
min_cost = optimal_merge(files)
print("Minimum cost of merging is:", min_cost, "Comparisons")

Minimum cost of merging is: 205 Comparisons