Design and Analysis Space Complexities

---

In this chapter, we will discuss the complexity of computational problems with respect to the amount of space an algorithm requires.

Space complexity shares many of the features of time complexity and serves as a further way of classifying problems according to their computational difficulties.

What is Space Complexity?

Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm.

We often speak of extra memory needed, not counting the memory needed to store the input itself. Again, we use natural (but fixed-length) units to measure this.

We can use bytes, but it's easier to use, say, the number of integers used, the number of fixed-sized structures, etc.

In the end, the function we come up with will be independent of the actual number of bytes needed to represent the unit.

Space complexity is sometimes ignored because the space used is minimal and/or obvious, however sometimes it becomes as important issue as time complexity

Definition

Let M be a deterministic Turing machine (TM) that halts on all inputs. The space complexity of M is the function $f \colon N \rightarrow N$, where f(n) is the maximum number of cells of tape and M scans any input of length M. If the space complexity of M is f(n), we can say that M runs in space f(n).

We estimate the space complexity of Turing machine by using asymptotic notation.

Let $f \colon N \rightarrow R^+$ be a function. The space complexity classes can be defined as follows −

SPACE = {L | L is a language decided by an O(f(n)) space deterministic TM}

SPACE = {L | L is a language decided by an O(f(n)) space non-deterministic TM}

PSPACE is the class of languages that are decidable in polynomial space on a deterministic Turing machine.

In other words, PSPACE = U_k SPACE (n^k)

Savitch’s Theorem

One of the earliest theorem related to space complexity is Savitch’s theorem. According to this theorem, a deterministic machine can simulate non-deterministic machines by using a small amount of space.

For time complexity, such a simulation seems to require an exponential increase in time. For space complexity, this theorem shows that any non-deterministic Turing machine that uses f(n) space can be converted to a deterministic TM that uses f²(n) space.

Hence, Savitch’s theorem states that, for any function, $f \colon N \rightarrow R^+$, where $f(n) \geqslant n$

NSPACE(f(n)) ⊆ SPACE(f(n))

Relationship Among Complexity Classes

The following diagram depicts the relationship among different complexity classes.

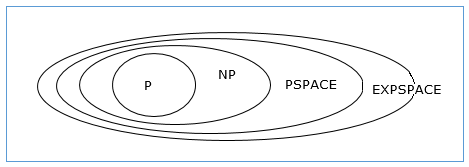
Till now, we have not discussed P and NP classes in this tutorial. These will be discussed later.