
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Dijkstra’s Shortest Path Algorithm
Dijkstra’s shortest path algorithm is similar to that of Prim’s algorithm as they both rely on finding the shortest path locally to achieve the global solution. However, unlike prim’s algorithm, the dijkstra’s algorithm does not find the minimum spanning tree; it is designed to find the shortest path in the graph from one vertex to other remaining vertices in the graph. Dijkstra’s algorithm can be performed on both directed and undirected graphs.
Since the shortest path can be calculated from single source vertex to all the other vertices in the graph, Dijkstra’s algorithm is also called single-source shortest path algorithm. The output obtained is called shortest path spanning tree.
In this chapter, we will learn about the greedy approach of the dijkstra’s algorithm.
Dijkstra’s Algorithm
The dijkstra’s algorithm is designed to find the shortest path between two vertices of a graph. These two vertices could either be adjacent or the farthest points in the graph. The algorithm starts from the source. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S. And the output is the shortest path spanning tree.
Algorithm
Declare two arrays − distance[] to store the distances from the source vertex to the other vertices in graph and visited[] to store the visited vertices.
Set distance[S] to ‘0’ and distance[v] = ∞, where v represents all the other vertices in the graph.
Add S to the visited[] array and find the adjacent vertices of S with the minimum distance.
The adjacent vertex to S, say A, has the minimum distance and is not in the visited array yet. A is picked and added to the visited array and the distance of A is changed from ∞ to the assigned distance of A, say d1, where d1 < ∞.
Repeat the process for the adjacent vertices of the visited vertices until the shortest path spanning tree is formed.
Examples
To understand the dijkstra’s concept better, let us analyze the algorithm with the help of an example graph −
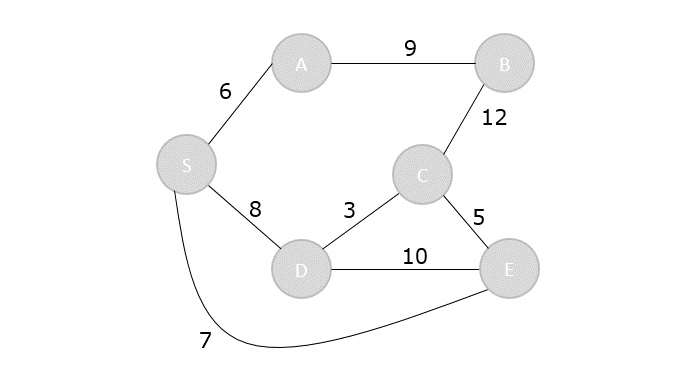
Step 1
Initialize the distances of all the vertices as ∞, except the source node S.
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
Now that the source vertex S is visited, add it into the visited array.
visited = {S}
Step 2
The vertex S has three adjacent vertices with various distances and the vertex with minimum distance among them all is A. Hence, A is visited and the dist[A] is changed from ∞ to 6.
S → A = 6 S → D = 8 S → E = 7
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | ∞ | ∞ | 8 | 7 |
Visited = {S, A}
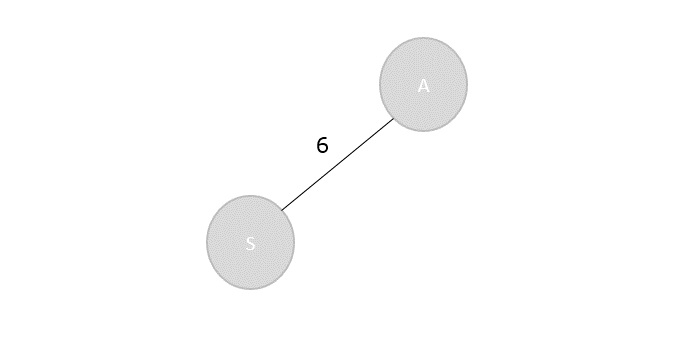
Step 3
There are two vertices visited in the visited array, therefore, the adjacent vertices must be checked for both the visited vertices.
Vertex S has two more adjacent vertices to be visited yet: D and E. Vertex A has one adjacent vertex B.
Calculate the distances from S to D, E, B and select the minimum distance −
S → D = 8 and S → E = 7. S → B = S → A + A → B = 6 + 9 = 15
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | ∞ | 8 | 7 |
Visited = {S, A, E}
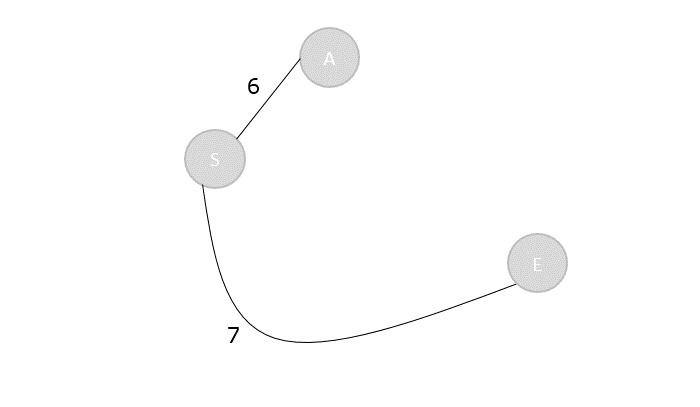
Step 4
Calculate the distances of the adjacent vertices – S, A, E – of all the visited arrays and select the vertex with minimum distance.
S → D = 8 S → B = 15 S → C = S → E + E → C = 7 + 5 = 12
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | 12 | 8 | 7 |
Visited = {S, A, E, D}
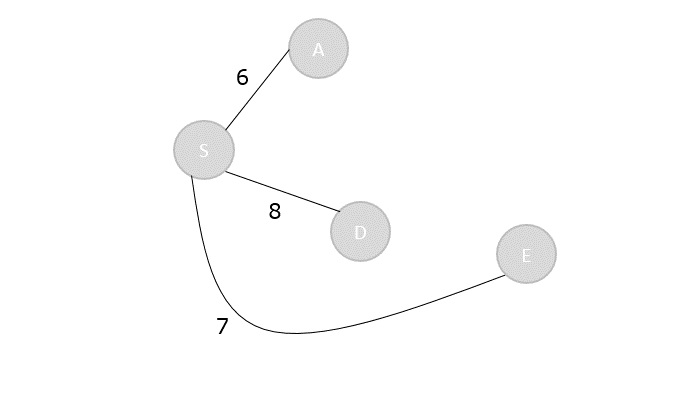
Step 5
Recalculate the distances of unvisited vertices and if the distances minimum than existing distance is found, replace the value in the distance array.
S → C = S → E + E → C = 7 + 5 = 12 S → C = S → D + D → C = 8 + 3 = 11
dist[C] = minimum (12, 11) = 11
S → B = S → A + A → B = 6 + 9 = 15 S → B = S → D + D → C + C → B = 8 + 3 + 12 = 23
dist[B] = minimum (15,23) = 15
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | 11 | 8 | 7 |
Visited = { S, A, E, D, C}
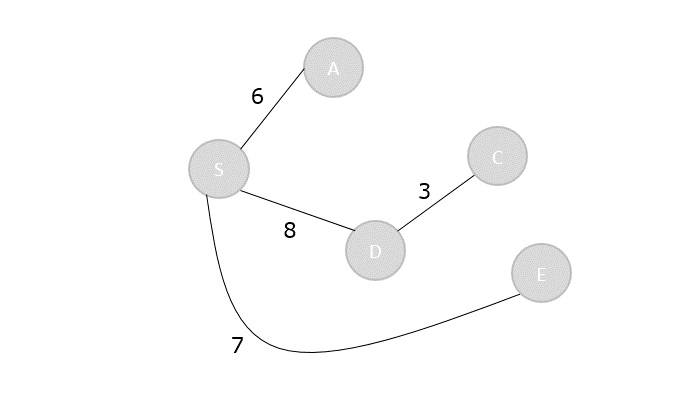
Step 6
The remaining unvisited vertex in the graph is B with the minimum distance 15, is added to the output spanning tree.
Visited = {S, A, E, D, C, B}
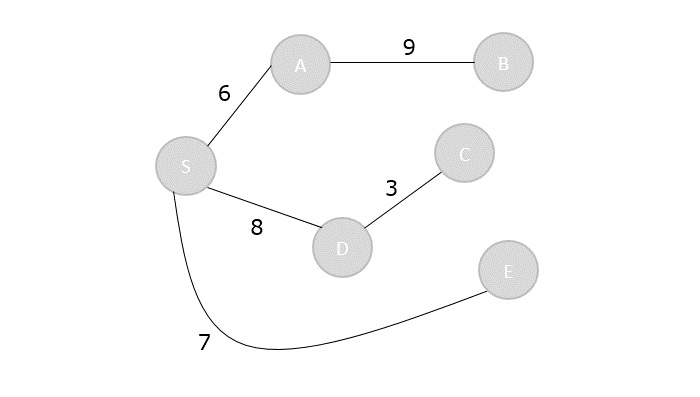
The shortest path spanning tree is obtained as an output using the dijkstra’s algorithm.
Example
The program implements the dijkstra’s shortest path problem that takes the cost adjacency matrix as the input and prints the shortest path as the output along with the minimum cost.
#include<stdio.h>
#include<limits.h>
#include<stdbool.h>
int min_dist(int[], bool[]);
void greedy_dijsktra(int[][6],int);
int min_dist(int dist[], bool visited[]){ // finding minimum dist
int minimum=INT_MAX,ind;
for(int k=0; k<6; k++) {
if(visited[k]==false && dist[k]<=minimum) {
minimum=dist[k];
ind=k;
}
}
return ind;
}
void greedy_dijsktra(int graph[6][6],int src){
int dist[6];
bool visited[6];
for(int k = 0; k<6; k++) {
dist[k] = INT_MAX;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for(int k = 0; k<6; k++) {
int m=min_dist(dist,visited);
visited[m]=true;
for(int k = 0; k<6; k++) {
// updating the dist of neighbouring vertex
if(!visited[k] && graph[m][k] && dist[m]!=INT_MAX && dist[m]+graph[m][k]<dist[k])
dist[k]=dist[m]+graph[m][k];
}
}
printf("Vertex\t\tdist from source vertex\n");
for(int k = 0; k<6; k++) {
char str=65+k;
printf("%c\t\t\t%d\n", str, dist[k]);
}
}
int main(){
int graph[6][6]= {
{0, 1, 2, 0, 0, 0},
{1, 0, 0, 5, 1, 0},
{2, 0, 0, 2, 3, 0},
{0, 5, 2, 0, 2, 2},
{0, 1, 3, 2, 0, 1},
{0, 0, 0, 2, 1, 0}
};
greedy_dijsktra(graph,0);
return 0;
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
#include<iostream>
#include<climits>
using namespace std;
int min_dist(int dist[], bool visited[]){ // finding minimum dist
int minimum=INT_MAX,ind;
for(int k=0; k<6; k++) {
if(visited[k]==false && dist[k]<=minimum) {
minimum=dist[k];
ind=k;
}
}
return ind;
}
void greedy_dijsktra(int graph[6][6],int src){
int dist[6];
bool visited[6];
for(int k = 0; k<6; k++) {
dist[k] = INT_MAX;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for(int k = 0; k<6; k++) {
int m=min_dist(dist,visited);
visited[m]=true;
for(int k = 0; k<6; k++) {
// updating the dist of neighbouring vertex
if(!visited[k] && graph[m][k] && dist[m]!=INT_MAX && dist[m]+graph[m][k]<dist[k])
dist[k]=dist[m]+graph[m][k];
}
}
cout<<"Vertex\t\tdist from source vertex"<<endl;
for(int k = 0; k<6; k++) {
char str=65+k;
cout<<str<<"\t\t\t"<<dist[k]<<endl;
}
}
int main(){
int graph[6][6]= {
{0, 1, 2, 0, 0, 0},
{1, 0, 0, 5, 1, 0},
{2, 0, 0, 2, 3, 0},
{0, 5, 2, 0, 2, 2},
{0, 1, 3, 2, 0, 1},
{0, 0, 0, 2, 1, 0}
};
greedy_dijsktra(graph,0);
return 0;
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
public class Main {
static int min_dist(int dist[], boolean visited[]) { // finding minimum dist
int minimum = Integer.MAX_VALUE;
int ind = -1;
for (int k = 0; k < 6; k++) {
if (!visited[k] && dist[k] <= minimum) {
minimum = dist[k];
ind = k;
}
}
return ind;
}
static void greedy_dijkstra(int graph[][], int src) {
int dist[] = new int[6];
boolean visited[] = new boolean[6];
for (int k = 0; k < 6; k++) {
dist[k] = Integer.MAX_VALUE;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for (int k = 0; k < 6; k++) {
int m = min_dist(dist, visited);
visited[m] = true;
for (int j = 0; j < 6; j++) {
// updating the dist of neighboring vertex
if (!visited[j] && graph[m][j] != 0 && dist[m] != Integer.MAX_VALUE
&& dist[m] + graph[m][j] < dist[j])
dist[j] = dist[m] + graph[m][j];
}
}
System.out.println("Vertex\t\tdist from source vertex");
for (int k = 0; k < 6; k++) {
char str = (char) (65 + k);
System.out.println(str + "\t\t\t" + dist[k]);
}
}
public static void main(String args[]) {
int graph[][] = { { 0, 1, 2, 0, 0, 0 }, { 1, 0, 0, 5, 1, 0 }, { 2, 0, 0, 2, 3, 0 },
{ 0, 5, 2, 0, 2, 2 }, { 0, 1, 3, 2, 0, 1 }, { 0, 0, 0, 2, 1, 0 } };
greedy_dijkstra(graph, 0);
}
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
import sys
def min_dist(dist, visited): # finding minimum dist
minimum = sys.maxsize
ind = -1
for k in range(6):
if not visited[k] and dist[k] <= minimum:
minimum = dist[k]
ind = k
return ind
def greedy_dijkstra(graph, src):
dist = [sys.maxsize] * 6
visited = [False] * 6
dist[src] = 0 # Source vertex dist is set 0
for _ in range(6):
m = min_dist(dist, visited)
visited[m] = True
for k in range(6):
# updating the dist of neighbouring vertex
if not visited[k] and graph[m][k] and dist[m] != sys.maxsize and dist[m] + graph[m][k] < dist[k]:
dist[k] = dist[m] + graph[m][k]
print("Vertex\t\tdist from source vertex")
for k in range(6):
str_val = chr(65 + k) # Convert index to corresponding character
print(str_val, "\t\t\t", dist[k])
# Main code
graph = [
[0, 1, 2, 0, 0, 0],
[1, 0, 0, 5, 1, 0],
[2, 0, 0, 2, 3, 0],
[0, 5, 2, 0, 2, 2],
[0, 1, 3, 2, 0, 1],
[0, 0, 0, 2, 1, 0]
]
greedy_dijkstra(graph, 0)
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
