Counting Sort Algorithm

Counting sort is an external sorting algorithm that assumes all the input values are integers that lie between the range 0 and k. Then mathematical computations on these input values to place them at the correct position in the output array.

This algorithm makes use of a counter to count the frequency of occurrence of the numbers and arrange them accordingly. Suppose, if a number ‘m’ occurs 5 times in the input sequence, the counter value of the number will become 5 and it is repeated 5 times in the output array.

Counting Sort Algorithm

The counting sort algorithm assumes that the input is relatively smaller so the algorithm is as follows −

Step 1 − Maintain two arrays, one with the size of input elements without repetition to store the count values and other with the size of the input array to store the output.

Step 2 − Initialize the count array with all zeroes and keep the output array empty.

Step 3 − Every time an element occurs in the input list, increment the corresponding counter value by 1, until it reaches the end of the input list.

Step 4 − Now, in the output array, every time a counter is greater than 0, add the element at its respective index, i.e. if the counter of ‘0’ is 2, ‘0’ added at the 2nd position (i.e. 1st index) of the output array. Then decrement the counter value by 1.

Step 5 − Repeat Step 4 until all the counter values become 0. The list obtained is the output list.

COUNTING-SORT(A, B, k)
let C[0 … k] be a new array
for i = 0 to k
C[i] = 0
for j = 1 to A.length
C[A[j]] = C[A[j]] + 1

// C[i] now contains the number of elements equal to i.
for i = 1 to k
C[i] = C[i] + C[i – 1]
// C[i] now contains the number of elements less than or equal to i.
for j = A.length downto 1
B[C[A[j]]] = A[j]
C[A[j]] = C[A[j – 1]

Analysis

The average case time complexity for the counting sort algorithm is same as bucket sort. It runs in Θ(n) time.

Example

Consider an input list to be sorted, 0, 2, 1, 4, 6, 2, 1, 1, 0, 3, 7, 7, 9.

For easier computations, let us start with single digit numbers.

Step 1

Create two arrays: to store counters and the output. Initialize the counter array with zeroes.

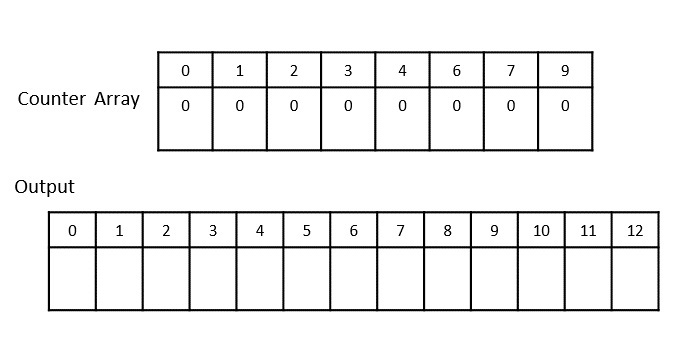
Step 2

After incrementing all the counter values until it reaches the end of the input list, we achieve −

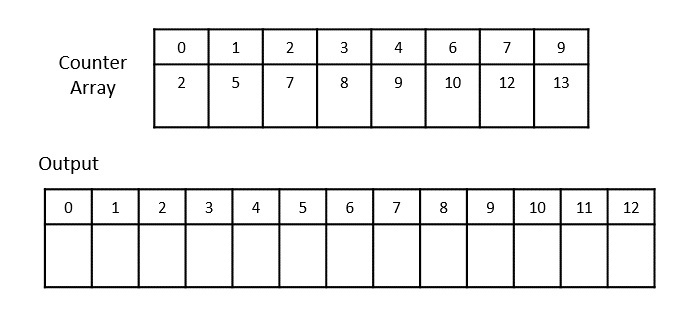
Step 3

Now, push the elements at the corresponding index in the output list.

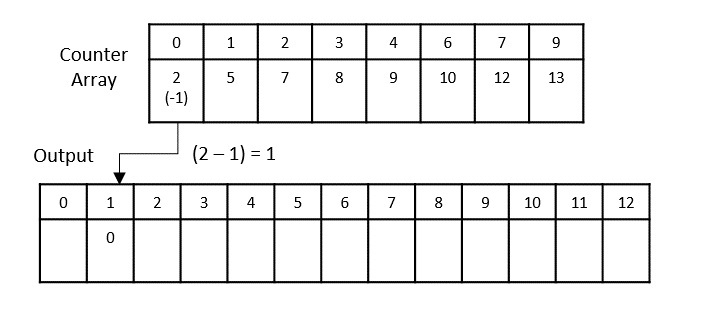
Step 4

Decrement the counter by 1 after adding the elements in the output array. Now, 1 is added at the 4^th index.

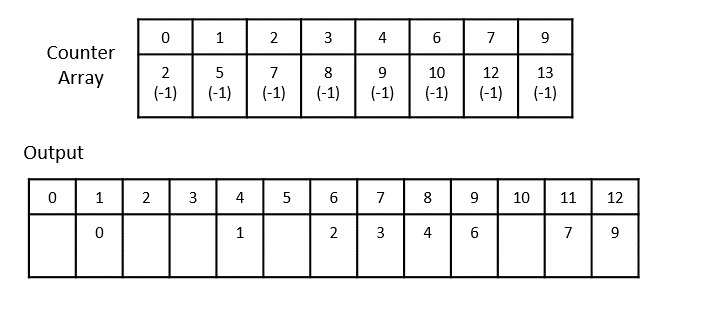
Step 5

Add the remaining values preceding the index in previous step.

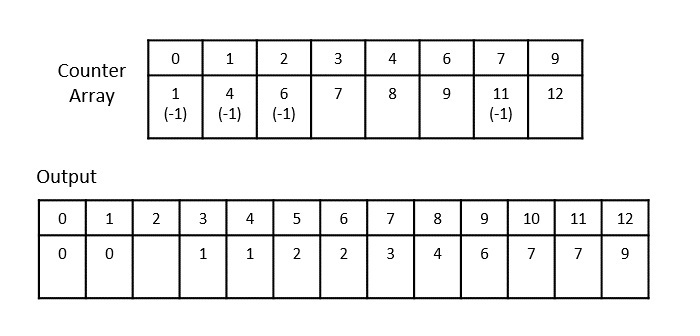
Step 6

After adding the last values, we get −

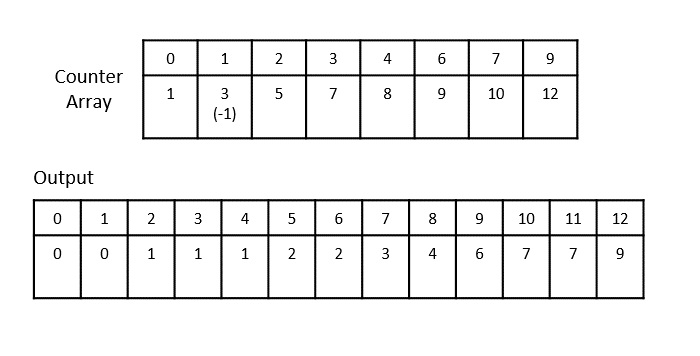
The final sorted output is achieved as 0, 0, 1, 1, 1, 2, 2, 3, 4, 6, 7, 7, 9

Implementation

The counting sort implementation works closely with the algorithm where we construct an array to store the frequency of each element of the input array. Based on these frequencies, the elements are placed in the output array. Repetitive elements are also sorted in the counting sort algorithm.

Example

In this chapter, we look into the counting sort program implemented in four different programming languages.

#include<stdio.h>
int countingsort(int a[], int n){
   int i, j;
   int output[15], c[100];
   for (i = 0; i < 100; i++)
      c[i] = 0;
   for (j = 0; j < n; j++)
      ++c[a[j]];
   for (i = 1; i <= 99; i++)
      c[i] += c[i-1];
   for (j = n-1; j >= 0; j--) {
      output[c[a[j]] - 1] = a[j];
      --c[a[j]];
   }
   printf("\nAfter sorting array elements are: ");
   for (i = 0; i<n; i++)
      printf("%d ", output[i]);
}
void main(){
   int n , i;
   int a[] = {12, 32, 44, 8, 16};
   n = sizeof(a) / sizeof(a[0]);
   printf("Before sorting array elements are: ");
   for(int i = 0; i<n; i++){
       printf("%d " , a[i]);
   }
   countingsort(a, n);
}

Before sorting array elements are: 12 32 44 8 16 
After sorting array elements are: 8 12 16 32 44

#include<iostream>
using namespace std;
void countingsort(int a[], int n){
   int i, j;
   int output[15], c[100];
   for (i = 0; i < 100; i++)
      c[i] = 0;
   for (j = 0; j < n; j++)
      ++c[a[j]];
   for (i = 1; i <= 99; i++)
      c[i] += c[i-1];
   for (j = n-1; j >= 0; j--) {
      output[c[a[j]] - 1] = a[j];
      --c[a[j]];
   }
   cout << "\nAfter sorting array elements are: ";
   for (i = 0; i <n; i++)
      cout << output[i] << " ";
}
int main(){
   int n , i;
   int a[] = {12, 32, 44, 8, 16};
   n = sizeof(a) / sizeof(a[0]);
   cout<<"Before sorting array elements are: ";
   for(int i = 0; i<n; i++){
       cout<<a[i]<<" ";
   }
   countingsort(a, n);
   cout << "\n";
   return 0;
}

Before sorting array elements are: 12 32 44 8 16 
After sorting array elements are: 8 12 16 32 44 

import java.io.*;
public class counting_sort {
   static void sort(int a[], int n) {
      int i, j;
      int output[] = new int[15];
      int c[] = new int[100];
      for (i = 0; i < 100; i++)
      c[i] = 0;
      for (j = 0; j < n; j++)
      ++c[a[j]];
      for (i = 1; i <= 99; i++)
      c[i] += c[i-1];
      for (j = n-1; j >= 0; j--) {
         output[c[a[j]] - 1] = a[j];
         --c[a[j]];
      }
      System.out.println("\nAfter sorting array elements are: ");
      for (i = 0; i < n; ++i)
      System.out.print(output[i] + " ");
   }
   public static void main(String args[]){
      int a[] = {12, 32, 44, 8, 16};
      int n = a.length;
      System.out.println("Before sorting array elements are: ");
      for(int i = 0; i<n; i++){
          System.out.print(a[i] + " ");
      }
      // Function call
      sort(a, n);
   }
}

Before sorting array elements are: 
12 32 44 8 16 
After sorting array elements are: 
8 12 16 32 44 

output = []
def counting_sort(a, n):
    output = [0] * n
    c = [0] * 100
    for i in range(100):
        c[i] = 0
    for j in range(n):
        c[a[j]] += 1
    for i in range(1, 99):
        c[i] += c[i-1]
    for j in range(n-1, -1, -1):
        output[c[a[j]] - 1] = a[j]
        c[a[j]] -= 1
    print("After sorting array elements are: ")
    print(output)
a = [12, 32, 44, 8, 16]
n = len(a)
print("Before sorting array elements are: ")
print (a)
counting_sort(a, n)

Before sorting array elements are: 
[12, 32, 44, 8, 16]
After sorting array elements are: 
[8, 12, 16, 32, 44]