Randomized Quick Sort Algorithm

Quicksort is a popular sorting algorithm that chooses a pivot element and sorts the input list around that pivot element. To learn more about quick sort, please click here.

Randomized quick sort is designed to decrease the chances of the algorithm being executed in the worst case time complexity of O(n²). The worst case time complexity of quick sort arises when the input given is an already sorted list, leading to n(n – 1) comparisons. There are two ways to randomize the quicksort −

• Randomly shuffling the inputs: Randomization is done on the input list so that the sorted input is jumbled again which reduces the time complexity. However, this is not usually performed in the randomized quick sort.

• Randomly choosing the pivot element: Making the pivot element a random variable is commonly used method in the randomized quick sort. Here, even if the input is sorted, the pivot is chosen randomly so the worst case time complexity is avoided.

Randomized Quick Sort Algorithm

The algorithm exactly follows the standard algorithm except it randomizes the pivot selection.

Pseudocode

partition-left(arr[], low, high)
   pivot = arr[high]
   i = low // place for swapping
   for j := low to high – 1 do
      if arr[j] <= pivot then
         swap arr[i] with arr[j]
         i = i + 1
   swap arr[i] with arr[high]
   return i

partition-right(arr[], low, high)
   r = Random Number from low to high
   Swap arr[r] and arr[high]
   return partition-left(arr, low, high)

quicksort(arr[], low, high)
   if low < high
      p = partition-right(arr, low, high)
      quicksort(arr, low , p-1)
      quicksort(arr, p+1, high)

Example

Let us look at an example to understand how randomized quicksort works in avoiding the worst case time complexity. Since, we are designing randomized algorithms to decrease the occurrence of worst cases in time complexity lets take a sorted list as an input for this example.

The sorted input list is 3, 5, 7, 8, 12, 15. We need to apply the quick sort algorithm to sort the list.

Step 1

Considering the worst case possible, if the random pivot chosen is also the highest index number, it compares all the other numbers and another pivot is selected.

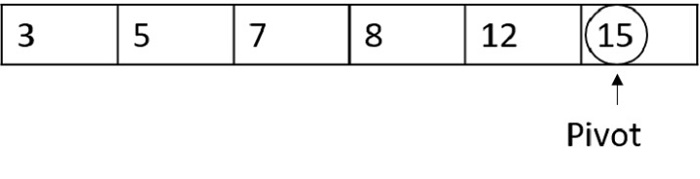
Since 15 is greater than all the other numbers in the list, it won’t be swapped, and another pivot is chosen.

Step 2

This time, if the random pivot function chooses 7 as the pivot number −

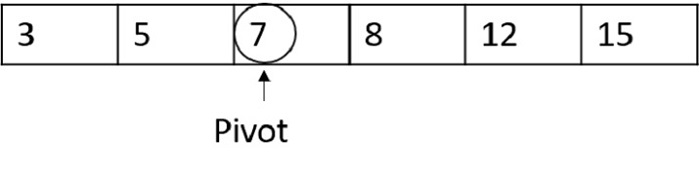
Now the pivot divides the list into half so standard quick sort is carried out usually. However, the time complexity is decreased than the worst case.

It is to be noted that the worst case time complexity of the quick sort will always remain O(n²) but with randomizations we are decreasing the occurrences of that worst case.

Implementation

Following are the implementations of the above approach in various programming langauges −

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to swap two elements
void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}
// Function to partition the array
int partition_left(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            swap(&arr[i], &arr[j]);
            i++;
        }
    }
    swap(&arr[i], &arr[high]);
    return i;
}
// Function to perform random partition
int partition_right(int arr[], int low, int high) {
    srand(time(NULL));
    int r = low + rand() % (high - low);
    swap(&arr[r], &arr[high]);
    return partition_left(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int p = partition_right(arr, low, high);
        quicksort(arr, low, p - 1);
        quicksort(arr, p + 1, high);
    }
}
// Function to print the array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}
// Driver code
int main() {
    int arr[] = { 6, 4, 12, 8, 15, 16};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("Original array: ");
    printArray(arr, n);
    quicksort(arr, 0, n - 1);
    printf("Sorted array: ");
    printArray(arr, n);
    return 0;
}

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16

#include <iostream>
#include <cstdlib>
#include <ctime>
// Function to swap two elements
void swap(int arr[], int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
// Function to partition the array
int partitionLeft(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            swap(arr, i, j);
            i++;
        }
    }
    swap(arr, i, high);
    return i;
}
// Function to perform random partition
int partitionRight(int arr[], int low, int high) {
    srand(time(NULL));
    int r = low + rand() % (high - low);
    swap(arr, r, high);
    return partitionLeft(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int p = partitionRight(arr, low, high);
        quicksort(arr, low, p - 1);
        quicksort(arr, p + 1, high);
    }
}
// Function to print the array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;
}
// Driver code
int main() {
    int arr[] = {6, 4, 12, 8, 15, 16};
    int n = sizeof(arr) / sizeof(arr[0]);
    std::cout << "Original array: ";
    printArray(arr, n);
    quicksort(arr, 0, n - 1);
    std::cout << "Sorted array: ";
    printArray(arr, n);
    return 0;
}

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16 

import java.util.Arrays;
import java.util.Random;
public class QuickSort {
    // Function to swap two elements
    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    // Function to partition the array
    static int partitionLeft(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = low;
        for (int j = low; j < high; j++) {
            if (arr[j] <= pivot) {
                swap(arr, i, j);
                i++;
            }
        }
        swap(arr, i, high);
        return i;
    }
    // Function to perform random partition
    static int partitionRight(int[] arr, int low, int high) {
        Random rand = new Random();
        int r = low + rand.nextInt(high - low);
        swap(arr, r, high);
        return partitionLeft(arr, low, high);
    }
    // Recursive function for quicksort
    static void quicksort(int[] arr, int low, int high) {
        if (low < high) {
            int p = partitionRight(arr, low, high);
            quicksort(arr, low, p - 1);
            quicksort(arr, p + 1, high);
        }
    }
    // Function to print the array
    static void printArray(int[] arr) {
        for (int element : arr) {
            System.out.print(element + " ");
        }
        System.out.println();
    }
    // Driver code
    public static void main(String[] args) {
        int[] arr = {6, 4, 12, 8, 15, 16};
        int n = arr.length;
        System.out.print("Original array: ");
        printArray(arr);
        quicksort(arr, 0, n - 1);
        System.out.print("Sorted array: ");
        printArray(arr);
    }
}

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16 

import random
# Function to partition the array
def partition_left(arr, low, high):
    pivot = arr[high]
    i = low
    for j in range(low, high):
        if arr[j] <= pivot:
            arr[i], arr[j] = arr[j], arr[i]
            i += 1
    arr[i], arr[high] = arr[high], arr[i]
    return i
# Function to perform random partition
def partition_right(arr, low, high):
    r = random.randint(low, high)
    arr[r], arr[high] = arr[high], arr[r]
    return partition_left(arr, low, high)
# Recursive function for quicksort
def quicksort(arr, low, high):
    if low < high:
        p = partition_right(arr, low, high)
        quicksort(arr, low, p - 1)
        quicksort(arr, p + 1, high)
# Function to print the array
def printArray(arr):
    for element in arr:
        print(element, end=" ")
    print()
# Driver code
arr = [6, 4, 12, 8, 15, 16]
n = len(arr)
print("Original array:", end=" ")
printArray(arr)
quicksort(arr, 0, n - 1)
print("Sorted array:", end=" ")
printArray(arr)

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16