Multistage Graph

Table of content

Multistage Graph

A multistage graph G = (V, E) is a directed graph where vertices are partitioned into k (where k > 1) number of disjoint subsets S = {s1,s2,…,sk} such that edge (u, v) is in E, then u Є si and v Є s1 + 1 for some subsets in the partition and |s1| = |sk| = 1.

The vertex s Є s1 is called the source and the vertex t Є sk is called sink.

G is usually assumed to be a weighted graph. In this graph, cost of an edge (i, j) is represented by c(i, j). Hence, the cost of path from source s to sink t is the sum of costs of each edges in this path.

The multistage graph problem is finding the path with minimum cost from source s to sink t.

Example

Consider the following example to understand the concept of multistage graph.

Multistage Graph

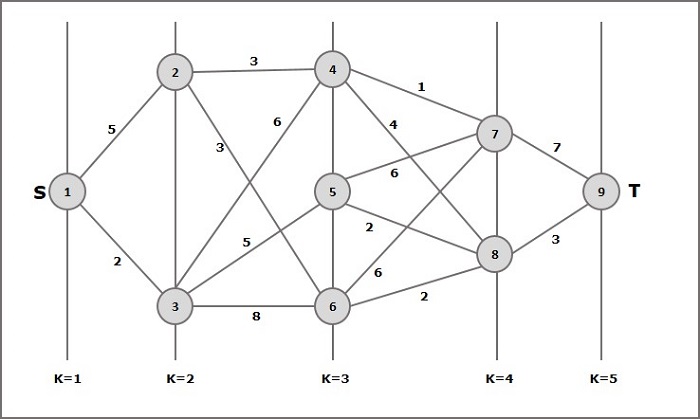
According to the formula, we have to calculate the cost (i, j) using the following steps

Step 1: Cost (K-2, j)

In this step, three nodes (node 4, 5. 6) are selected as j. Hence, we have three options to choose the minimum cost at this step.

Cost(3, 4) = min {c(4, 7) + Cost(7, 9),c(4, 8) + Cost(8, 9)} = 7

Cost(3, 5) = min {c(5, 7) + Cost(7, 9),c(5, 8) + Cost(8, 9)} = 5

Cost(3, 6) = min {c(6, 7) + Cost(7, 9),c(6, 8) + Cost(8, 9)} = 5

Step 2: Cost (K-3, j)

Two nodes are selected as j because at stage k - 3 = 2 there are two nodes, 2 and 3. So, the value i = 2 and j = 2 and 3.

Cost(2, 2) = min {c(2, 4) + Cost(4, 8) + Cost(8, 9),c(2, 6) +

Cost(6, 8) + Cost(8, 9)} = 8

Cost(2, 3) = {c(3, 4) + Cost(4, 8) + Cost(8, 9), c(3, 5) + Cost(5, 8)+ Cost(8, 9), c(3, 6) + Cost(6, 8) + Cost(8, 9)} = 10

Step 3: Cost (K-4, j)

Cost (1, 1) = {c(1, 2) + Cost(2, 6) + Cost(6, 8) + Cost(8, 9), c(1, 3) + Cost(3, 5) + Cost(5, 8) + Cost(8, 9))} = 12

c(1, 3) + Cost(3, 6) + Cost(6, 8 + Cost(8, 9))} = 13

Hence, the path having the minimum cost is 1→ 3→ 5→ 8→ 9.

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <limits.h>
// Function to find the minimum cost path in the multistage graph
typedef struct {
   int *path;
   int length;
} Result;
Result multistage_graph(int graph[][2], int num_edges, int num_vertices, int stages[][3], int num_stages) {
   // Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
   int *min_costs = (int *)malloc(num_vertices * sizeof(int));
   int *next_vertex = (int *)malloc(num_vertices * sizeof(int));
   for (int i = 0; i < num_vertices; i++) {
      min_costs[i] = INT_MAX;
      next_vertex[i] = -1;
   }
   // Initialize the minimum cost for the sink vertex to 0
   min_costs[num_vertices - 1] = 0;
   // Traverse the graph in reverse order starting from the second-last stage
   for (int i = num_stages - 2; i >= 0; i--) {
      for (int j = 0; j < num_vertices; j++) {
         if (stages[i][0] == j || stages[i][1] == j || stages[i][2] == j) {
            for (int k = 0; k < num_edges; k++) {
               if (graph[k][0] == j) {
                  int neighbor = graph[k][1];
                  int cost = graph[k][2] + min_costs[neighbor];
                  if (cost < min_costs[j]) {
                     // Update the minimum cost and next vertex for the current vertex
                     min_costs[j] = cost;
                     next_vertex[j] = neighbor;
                  }
               }
            }
         }
      }
   }
   // Reconstruct the minimum cost path from source to sink
   int *path = (int *)malloc(num_vertices * sizeof(int));
   int current_vertex = 0; // Start from the source vertex
   int path_length = 0;
   while (current_vertex != -1) {
       path[path_length++] = current_vertex;
       current_vertex = next_vertex[current_vertex];
   }
   // Free the dynamically allocated memory for min_costs and next_vertex
   free(min_costs);
   free(next_vertex);
   // Store the result in a Result structure
   Result result;
   result.path = path;
   result.length = path_length;
   return result;
}
int main() {
   // Define the multistage graph represented as an adjacency list
   int graph[][2] = {
      {0, 1}, {0, 2},
      {1, 3}, {1, 4},
      {2, 3}, {2, 4},
      {3, 5},
      {4, 5},
      {5, 6},
      {6, 7},
      {7, 8}
   };
   int num_edges = sizeof(graph) / sizeof(graph[0]);
   // Define the stages of the multistage graph
   int stages[][3] = {
      {8},       // Sink stage
      {6, 7},    // Stage K-1
      {3, 4, 5}, // Stage K-2
      {1, 2}     // Source stage
   };
   int num_stages = sizeof(stages) / sizeof(stages[0]);
   int num_vertices = 9; // Total number of vertices in the graph
   // Find the minimum cost path and cost using the multistage_graph function
   Result result = multistage_graph(graph, num_edges, num_vertices, stages, num_stages);
   // Print the result
   printf("Minimum cost path: ");
   for (int i = 0; i < result.length; i++) {
      printf("%d ", result.path[i]);
   }
   printf("\nMinimum cost: %d\n", result.path[result.length - 1]);
   // Free the dynamically allocated memory for the path
   free(result.path);
   return 0;
}

Output

Minimum cost path: 0 2 
Minimum cost: 2

#include <iostream>
#include <vector>
#include <unordered_map>
#include <limits>
using namespace std;
// Function to find the minimum cost path in the multistage graph
pair<vector<int>, int> multistage_graph(unordered_map<int, unordered_map<int, int>>& graph, vector<vector<int>>& stages) {
   int num_stages = stages.size();
   int num_vertices = graph.size();
   // Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
   vector<int> min_costs(num_vertices, numeric_limits<int>::max());
   vector<int> next_vertex(num_vertices, -1);
   // Initialize the minimum cost for the sink vertex to 0
   min_costs[num_vertices - 1] = 0;
   // Traverse the graph in reverse order starting from the second-last stage
   for (int i = num_stages - 2; i >= 0; i--) {
      for (int vertex : stages[i]) {
         for (auto neighbor : graph[vertex]) {
            int cost = neighbor.second + min_costs[neighbor.first];
            if (cost < min_costs[vertex]) {
               // Update the minimum cost and next vertex for the current vertex
               min_costs[vertex] = cost;
               next_vertex[vertex] = neighbor.first;
            }
         }
      }
   }
   // Reconstruct the minimum cost path from source to sink
   vector<int> path;
   int current_vertex = 0; // Start from the source vertex
   while (current_vertex != -1) {
      path.push_back(current_vertex);
      current_vertex = next_vertex[current_vertex];
   }
   // Return the path and the minimum cost as a pair
   return std::make_pair(path, min_costs[0]);
}
int main() {
   // Define the multistage graph represented as an adjacency map
   unordered_map<int, unordered_map<int, int>> graph = {
      {0, {{1, 2}, {2, 3}}},
      {1, {{3, 5}, {4, 2}}},
      {2, {{3, 4}, {4, 1}}},
      {3, {{5, 6}}},
      {4, {{5, 3}}},
      {5, {{6, 1}}},
      {6, {{7, 1}}},
      {7, {{8, 1}}},
      {8, {}}
   };
   // Define the stages of the multistage graph
   vector<vector<int>> stages = {
      {8},          // Sink stage
      {6, 7},       // Stage K-1
      {3, 4, 5},    // Stage K-2
      {1, 2}        // Source stage
   };
   // Find the minimum cost path and cost using the multistage_graph function
   auto result = multistage_graph(graph, stages);
   // Print the result
   cout << "Minimum cost path: ";
   for (int vertex : result.first) {
      cout << vertex << " ";
   }
   cout << std::endl;
   cout << "Minimum cost: " << result.second << endl;
   return 0;
}

Output

Minimum cost path: 0 
Minimum cost: 2147483647

import java.util.*;
public class Main {
   // Function to find the minimum cost path in the multistage graph
   static class Result {
      List<Integer> path;
      int cost;
      
      Result(List<Integer> path, int cost) {
         this.path = path;
         this.cost = cost;
      }
   }
   static Result multistage_graph(HashMap<Integer, HashMap<Integer, Integer>> graph, List<List<Integer>> stages) {
      int num_stages = stages.size();
      int num_vertices = graph.size();
      // Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
      List<Integer> min_costs = new ArrayList<>(Collections.nCopies(num_vertices, Integer.MAX_VALUE));
      List<Integer> next_vertex = new ArrayList<>(Collections.nCopies(num_vertices, -1));
      // Initialize the minimum cost for the sink vertex to 0
      min_costs.set(num_vertices - 1, 0);
      // Traverse the graph in reverse order starting from the second-last stage
      for (int i = num_stages - 2; i >= 0; i--) {
         for (int vertex : stages.get(i)) {
            for (Map.Entry<Integer, Integer> neighbor : graph.get(vertex).entrySet()) {
               int cost = neighbor.getValue() + min_costs.get(neighbor.getKey());
               if (cost < min_costs.get(vertex)) {
                  // Update the minimum cost and next vertex for the current vertex
                  min_costs.set(vertex, cost);
                  next_vertex.set(vertex, neighbor.getKey());
               }
            }
         }
      }
      // Reconstruct the minimum cost path from source to sink
      List<Integer> path = new ArrayList<>();
      int current_vertex = 0; // Start from the source vertex
      while (current_vertex != -1) {
          path.add(current_vertex);
          current_vertex = next_vertex.get(current_vertex);
      }
      // Return the path and the minimum cost as a Result object
      return new Result(path, min_costs.get(0));
   }
public static void main(String[] args) {
   // Define the multistage graph represented as an adjacency map
   HashMap<Integer, HashMap<Integer, Integer>> graph = new HashMap<>();
   graph.put(0, new HashMap<>());
   graph.get(0).put(1, 2);
   graph.get(0).put(2, 3);
   graph.put(1, new HashMap<>());
   graph.get(1).put(3, 5);
   graph.get(1).put(4, 2);
   graph.put(2, new HashMap<>());
   graph.get(2).put(3, 4);
   graph.get(2).put(4, 1);
   graph.put(3, new HashMap<>());
   graph.get(3).put(5, 6);
   graph.put(4, new HashMap<>());
   graph.get(4).put(5, 3);
   graph.put(5, new HashMap<>());
   graph.get(5).put(6, 1);
   graph.put(6, new HashMap<>());
   graph.get(6).put(7, 1);
   graph.put(7, new HashMap<>());
   graph.get(7).put(8, 1);
   graph.put(8, new HashMap<>());
   // Define the stages of the multistage graph
   List<List<Integer>> stages = new ArrayList<>();
   stages.add(Collections.singletonList(8));      // Sink stage
   stages.add(Arrays.asList(6, 7));               // Stage K-1
   stages.add(Arrays.asList(3, 4, 5));            // Stage K-2
   stages.add(Arrays.asList(1, 2));               // Source stage
   // Find the minimum cost path and cost using the multistage_graph function
   Result result = multistage_graph(graph, stages);
   // Print the result
   System.out.print("Minimum cost path: ");
   for (int vertex : result.path) {
      System.out.print(vertex + " \n");
   }
   System.out.println();
   System.out.println("Minimum cost: " + result.cost);
   }
}

Output

Minimum cost path: 0 

Minimum cost: 2147483647s

def multistage_graph(graph, stages):
    num_stages = len(stages)
    num_vertices = len(graph)
    # Create a list to store the minimum costs for each vertex
    min_costs = [float('inf')] * num_vertices
    # Create a list to store the next vertex in the path for each vertex
    next_vertex = [None] * num_vertices
    # Initialize the minimum cost for the sink vertex
    min_costs[-1] = 0
    # Traverse the graph in reverse order
    for i in range(num_stages - 2, -1, -1):
        for vertex in stages[i]:
            # Calculate the minimum cost and next vertex for the current vertex
            for neighbor in graph[vertex]:
                cost = graph[vertex][neighbor] + min_costs[neighbor]
                if cost < min_costs[vertex]:
                    min_costs[vertex] = cost
                    next_vertex[vertex] = neighbor

    # Reconstruct the minimum cost path
    path = []
    current_vertex = 0  # Start from the source vertex
    while current_vertex is not None:
        path.append(current_vertex)
        current_vertex = next_vertex[current_vertex]
    return path, min_costs[0]
# Example usage:
if __name__ == "__main__":
    # The multistage graph represented as an adjacency dictionary
    graph = {
        0: {1: 2, 2: 3},
        1: {3: 5, 4: 2},
        2: {3: 4, 4: 1},
        3: {5: 6},
        4: {5: 3},
        5: {6: 1},
        6: {7: 1},
        7: {8: 1},
        8: {}
    }
    # Define the stages of the multistage graph
    stages = [
        [8],          # Sink stage
        [6, 7],       # Stage K-1
        [3, 4, 5],    # Stage K-2
        [1, 2]        # Source stage
    ]
    path, min_cost = multistage_graph(graph, stages)
    print("Minimum cost path:", path)
    print("Minimum cost:", min_cost)

Output

Minimum cost path: [0]
Minimum cost: inf
Advertisements