Heap Sort Algorithm

Heap Sort is an efficient sorting technique based on the heap data structure.

The heap is a nearly-complete binary tree where the parent node could either be minimum or maximum. The heap with minimum root node is called min-heap and the root node with maximum root node is called max-heap. The elements in the input data of the heap sort algorithm are processed using these two methods.

The heap sort algorithm follows two main operations in this procedure −

• Builds a heap H from the input data using the heapify (explained further into the chapter) method, based on the way of sorting – ascending order or descending order.

• Deletes the root element of the root element and repeats until all the input elements are processed.

The heap sort algorithm heavily depends upon the heapify method of the binary tree. So what is this heapify method?

Heapify Method

The heapify method of a binary tree is to convert the tree into a heap data structure. This method uses recursion approach to heapify all the nodes of the binary tree.

Note − The binary tree must always be a complete binary tree as it must have two children nodes always.

The complete binary tree will be converted into either a max-heap or a min-heap by applying the heapify method.

To know more about the heapify algorithm, please click here.

Heap Sort Algorithm

As described in the algorithm below, the sorting algorithm first constructs the heap ADT by calling the Build-Max-Heap algorithm and removes the root element to swap it with the minimum valued node at the leaf. Then the heapify method is applied to rearrange the elements accordingly.

Algorithm: Heapsort(A)
BUILD-MAX-HEAP(A)
for i = A.length downto 2
exchange A[1] with A[i]
A.heap-size = A.heap-size - 1
MAX-HEAPIFY(A, 1)

Analysis

The heap sort algorithm is the combination of two other sorting algorithms: insertion sort and merge sort.

The similarities with insertion sort include that only a constant number of array elements are stored outside the input array at any time.

The time complexity of the heap sort algorithm is O(nlogn), similar to merge sort.

Example

Let us look at an example array to understand the sort algorithm better −

Building a heap using the BUILD-MAX-HEAP algorithm from the input array −

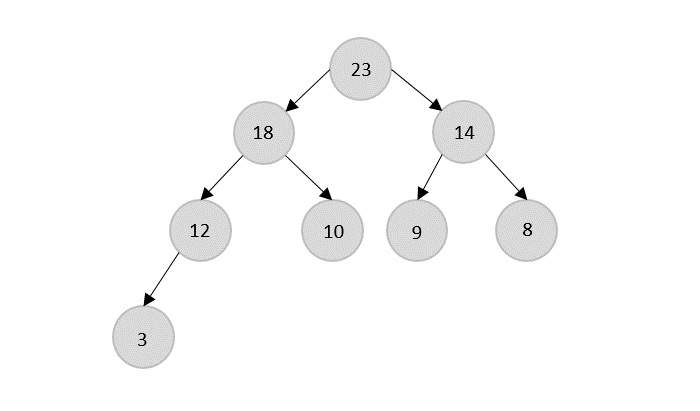
Rearrange the obtained binary tree by exchanging the nodes such that a heap data structure is formed.

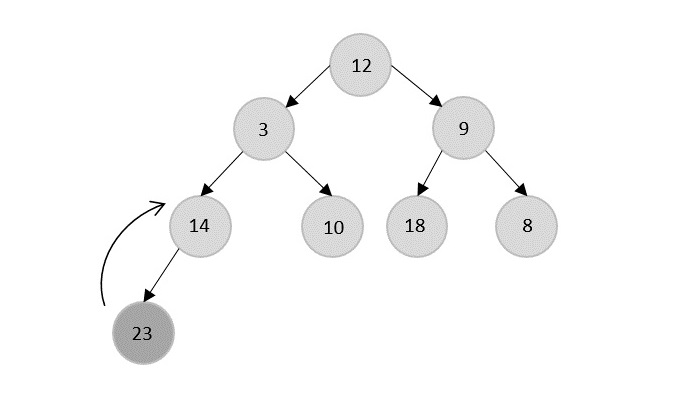
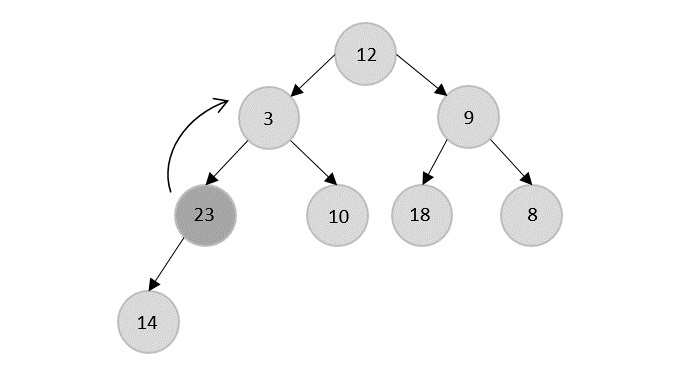
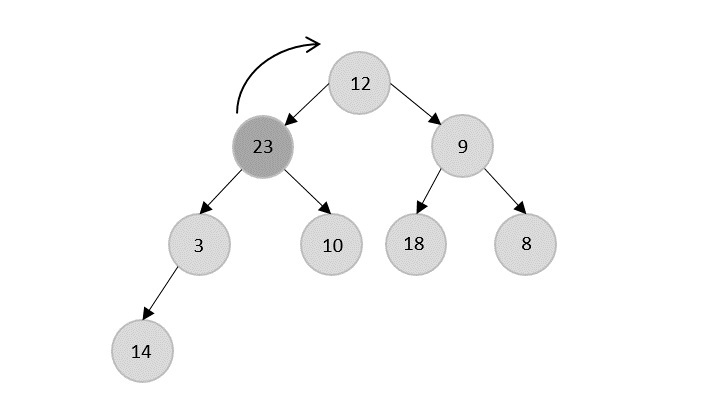
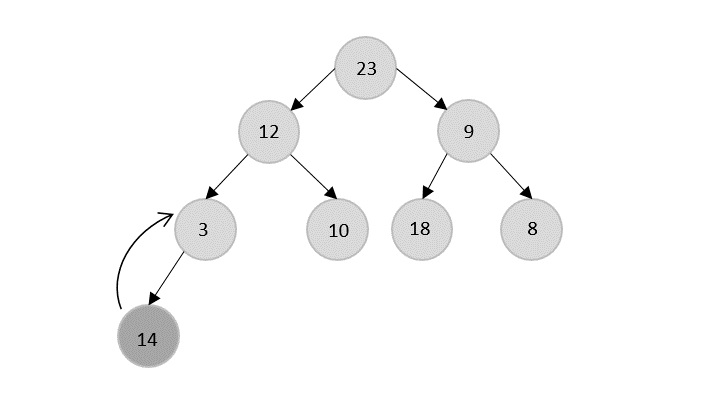
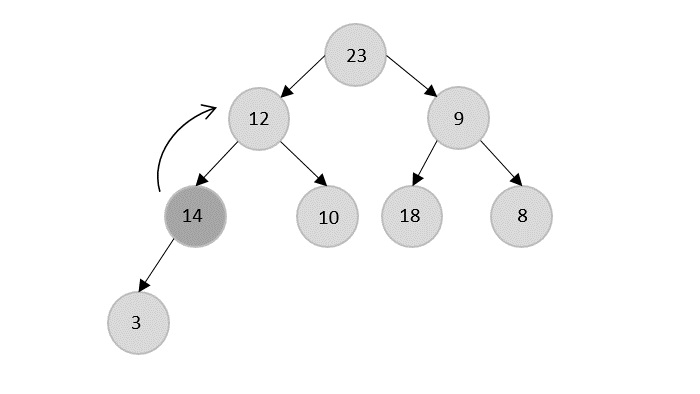
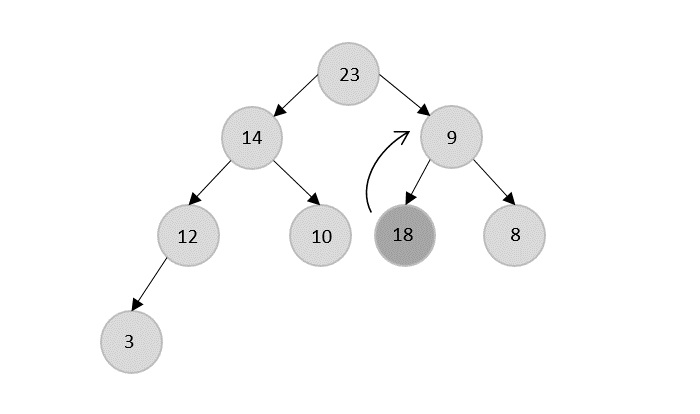
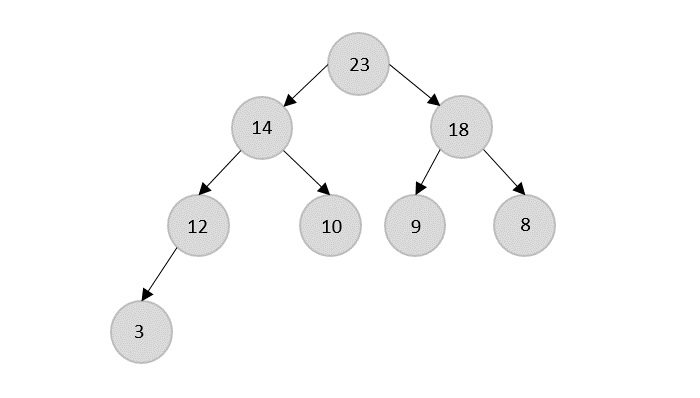
The Heapify Algorithm

Applying the heapify method, remove the root node from the heap and replace it with the next immediate maximum valued child of the root.

The root node is 23, so 23 is popped and 18 is made the next root because it is the next maximum node in the heap.

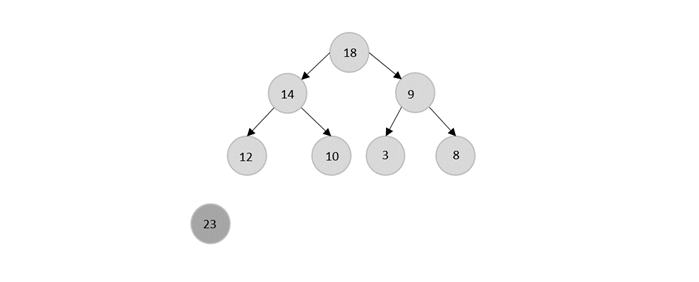
Now, 18 is popped after 23 which is replaced by 14.

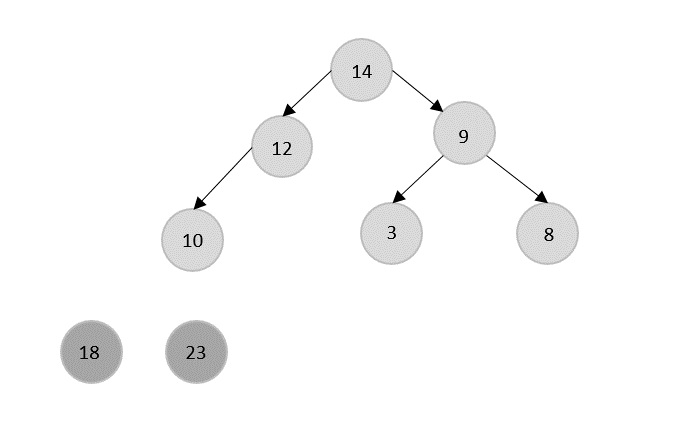
The current root 14 is popped from the heap and is replaced by 12.

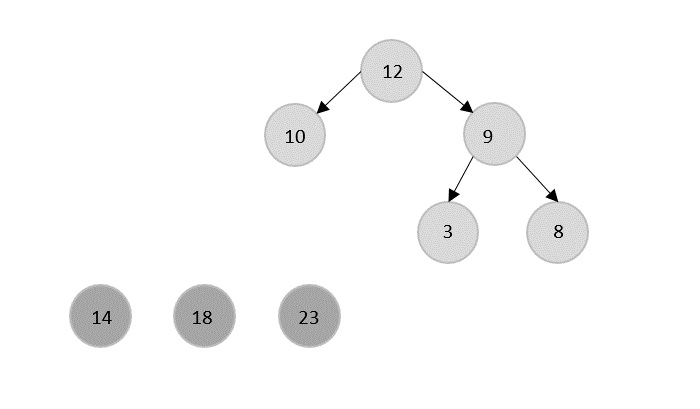
12 is popped and replaced with 10.

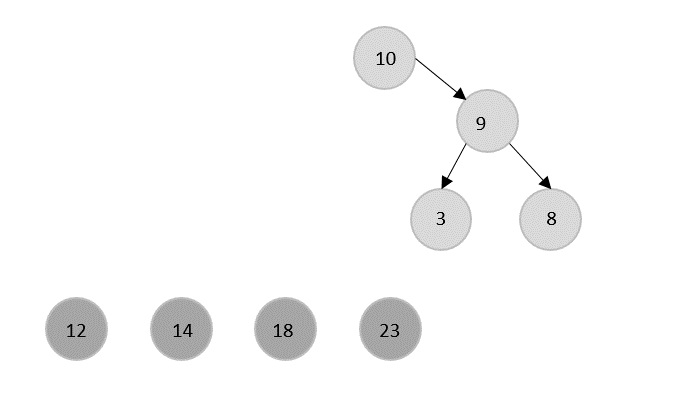
Similarly all the other elements are popped using the same process.

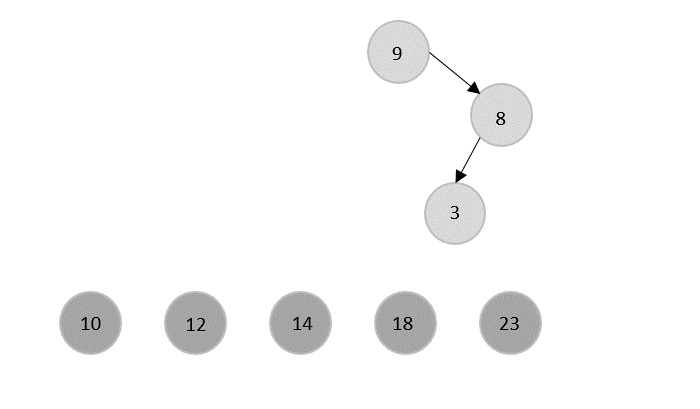
Here the current root element 9 is popped and the elements 8 and 3 are remained in the tree.

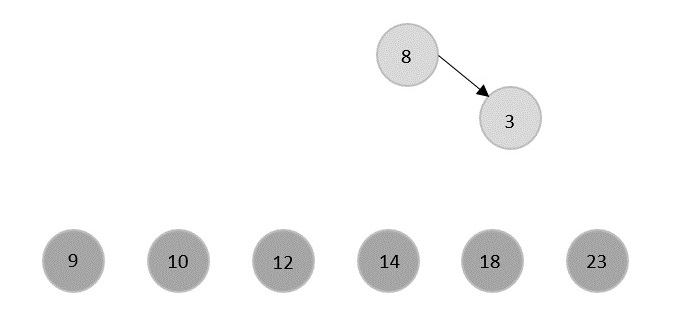
Then, 8 will be popped leaving 3 in the tree.

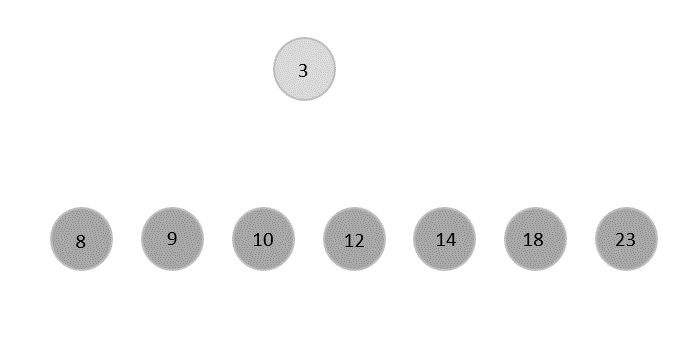
After completing the heap sort operation on the given heap, the sorted elements are displayed as shown below −

Every time an element is popped, it is added at the beginning of the output array since the heap data structure formed is a max-heap. But if the heapify method converts the binary tree to the min-heap, add the popped elements are on the end of the output array.

The final sorted list is,

Implementation

The logic applied on the implementation of the heap sort is: firstly, the heap data structure is built based on the max-heap property where the parent nodes must have greater values than the child nodes. Then the root node is popped from the heap and the next maximum node on the heap is shifted to the root. The process is continued iteratively until the heap is empty.

In this tutorial, we show the heap sort implementation in four different programming languages.

#include <stdio.h>
void heapify(int[], int);
void build_maxheap(int heap[], int n){
   int i, j, c, r, t;
   for (i = 1; i < n; i++) {
      c = i;
      do {
         r = (c - 1) / 2;
         if (heap[r] < heap[c]) { // to create MAX heap array
            t = heap[r];
            heap[r] = heap[c];
            heap[c] = t;
         }
         c = r;
      } while (c != 0);
   }
   printf("Heap array: ");
   for (i = 0; i < n; i++)
      printf("%d ", heap[i]);
   heapify(heap, n);
}
void heapify(int heap[], int n){
   int i, j, c, root, temp;
   for (j = n - 1; j >= 0; j--) {
      temp = heap[0];
      heap[0] = heap[j]; // swap max element with rightmost leaf element
      heap[j] = temp;
      root = 0;
      do {
         c = 2 * root + 1; // left node of root element
         if ((heap[c] < heap[c + 1]) && c < j-1)
            c++;
         if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
            temp = heap[root];
            heap[root] = heap[c];
            heap[c] = temp;
         }
         root = c;
      } while (c < j);
   }
   printf("\nThe sorted array is: ");
   
   for (i = 0; i < n; i++)
      printf("%d ", heap[i]);
}
int main(){
   int n, i, j, c, root, temp;
   n = 5;
   int heap[10] = {2, 3, 1, 0, 4}; // initialize the array
   build_maxheap(heap, n);
}

Heap array: 4 3 1 0 2 
The sorted array is: 0 1 2 3 4 

#include <iostream>
using namespace std;
void heapify(int[], int);
void build_maxheap(int heap[], int n){
   int i, j, c, r, t;
   for (i = 1; i < n; i++) {
      c = i;
      do {
         r = (c - 1) / 2;
         if (heap[r] < heap[c]) { // to create MAX heap array
            t = heap[r];
            heap[r] = heap[c];
            heap[c] = t;
         }
         c = r;
      } while (c != 0);
   }
   cout << "Heap array: ";
   for (i = 0; i < n; i++)
      cout <<heap[i]<<" ";
   heapify(heap, n);
}
void heapify(int heap[], int n){
   int i, j, c, root, temp;
   for (j = n - 1; j >= 0; j--) {
      temp = heap[0];
      heap[0] = heap[j]; // swap max element with rightmost leaf element
      heap[j] = temp;
      root = 0;
      do {
         c = 2 * root + 1; // left node of root element
         if ((heap[c] < heap[c + 1]) && c < j-1)
            c++;
         if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
            temp = heap[root];
            heap[root] = heap[c];
            heap[c] = temp;
         }
         root = c;
      } while (c < j);
   }
   cout << "\nThe sorted array is : ";
   for (i = 0; i < n; i++)
      cout <<heap[i]<<" ";
}
int main(){
   int n, i, j, c, root, temp;
   n = 5;
   int heap[10] = {2, 3, 1, 0, 4}; // initialize the array
   build_maxheap(heap, n);
   return 0;
}

Heap array: 4 3 1 0 2 
The sorted array is : 0 1 2 3 4 

import java.io.*;
public class HeapSort {
   static void build_maxheap(int heap[], int n) {
      for (int i = 1; i < n; i++) {
         int c = i;
         do {
            int r = (c - 1) / 2;
            if (heap[r] < heap[c]) { // to create MAX heap array
               int t = heap[r];
               heap[r] = heap[c];
               heap[c] = t;
            }
            c = r;
         } while (c != 0);
      }
      System.out.println("Heap array: ");
      for (int i = 0; i < n; i++) {
         System.out.print(heap[i] + " ");
      }
      heapify(heap, n);
   }
   static void heapify(int heap[], int n) {
      for (int j = n - 1; j >= 0; j--) {
         int c;
         int temp = heap[0];
         heap[0] = heap[j]; // swap max element with rightmost leaf element
         heap[j] = temp;
         int root = 0;
         do {
            c = 2 * root + 1; // left node of root element
            if ((heap[c] < heap[c + 1]) && c < j-1)
               c++;
            if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
               temp = heap[root];
               heap[root] = heap[c];
               heap[c] = temp;
            }
            root = c;
         } while (c < j);
      }
      System.out.println("\nThe sorted array is: ");
      for (int i = 0; i < n; i++) {
         System.out.print(heap[i] + " ");
      }
   }
   public static void main(String args[]) {
      int heap[] = new int[10];
      heap[0] = 4;
      heap[1] = 3;
      heap[2] = 1;
      heap[3] = 0;
      heap[4] = 2;
      int n = 5;
      build_maxheap(heap, n);
   }
}

Heap array: 
4 3 1 0 2 
The sorted array is: 
0 1 2 3 4 

def heapify(heap, n, i):
   maximum = i
   l = 2 * i + 1
   r = 2 * i + 2
   # if left child exists
   if l < n and heap[i] < heap[l]:
      maximum = l
   # if right child exits
   if r < n and heap[maximum] < heap[r]:
      maximum = r
   # root
   if maximum != i:
      heap[i],heap[maximum] = heap[maximum],heap[i] # swap root.
      heapify(heap, n, maximum)
def heapSort(heap):
   n = len(heap)
   # maxheap
   for i in range(n, -1, -1):
      heapify(heap, n, i)
   # element extraction
   for i in range(n-1, 0, -1):
      heap[i], heap[0] = heap[0], heap[i] # swap
      heapify(heap, i, 0)
# main
heap = [4, 3, 1, 0, 2]
heapSort(heap)
n = len(heap)
print("Heap array: ")
print(heap)
print ("The Sorted array is: ")
print(heap)

Heap array: 
[0, 1, 2, 3, 4]
The Sorted array is: 
[0, 1, 2, 3, 4]