
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Travelling Salesman Problem (Dynamic Approach)
Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.
However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.
Travelling Salesman Dynamic Programming Algorithm
Let us consider a graph G = (V,E), where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v), which should be non-negative.
Suppose we have started at city 1 and after visiting some cities now we are in city j. Hence, this is a partial tour. We certainly need to know j, since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.
For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1, and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j.
When |S|> 1 , we define 𝑪C(S,1)= $\propto$ since the path cannot start and end at 1.
Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j. We should select the next city in such a way that
$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$
Algorithm: Traveling-Salesman-Problem
C ({1}, 1) = 0
for s = 2 to n do
for all subsets S є {1, 2, 3, … , n} of size s and containing 1
C (S, 1) = ∞
for all j є S and j ≠ 1
C (S, j) = min {C (S – {j}, i) + d(i, j) for i є S and i ≠ j}
Return minj C ({1, 2, 3, …, n}, j) + d(j, i)
Analysis
There are at the most 2n.n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2n.n2).
Example
In the following example, we will illustrate the steps to solve the travelling salesman problem.
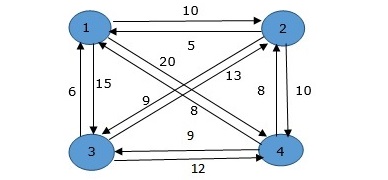
From the above graph, the following table is prepared.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 10 | 15 | 20 |
| 2 | 5 | 0 | 9 | 10 |
| 3 | 6 | 13 | 0 | 12 |
| 4 | 8 | 8 | 9 | 0 |
S = $\Phi$
$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$
$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$
$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$
S = 1
$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$
$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$
$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$
$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$
$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$
$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$
$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$
S = 2
$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$
$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$
$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$
S = 3
$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$
The minimum cost path is 35.
Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.
When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Implementation
Following are the implementations of the above approach in various programming languages −
#include <stdio.h>
#include <limits.h>
#define MAX 9999
int n = 4;
int distan[20][20] = {
{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}};
int DP[32][8];
int TSP(int mark, int position) {
int completed_visit = (1 << n) - 1;
if (mark == completed_visit) {
return distan[position][0];
}
if (DP[mark][position] != -1) {
return DP[mark][position];
}
int answer = MAX;
for (int city = 0; city < n; city++) {
if ((mark & (1 << city)) == 0) {
int newAnswer = distan[position][city] + TSP(mark | (1 << city), city);
answer = (answer < newAnswer) ? answer : newAnswer;
}
}
return DP[mark][position] = answer;
}
int main() {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
DP[i][j] = -1;
}
}
printf("Minimum Distance Travelled -> %d\n", TSP(1, 0));
return 0;
}
Output
Minimum Distance Travelled -> 122
#include<iostream>
using namespace std;
#define MAX 9999
int n=4;
int distan[20][20] = {{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}
};
int completed_visit = (1<<n) -1;
int DP[32][8];
int TSP(int mark, int position){
if(mark==completed_visit) {
return distan[position][0];
}
if(DP[mark][position]!=-1) {
return DP[mark][position];
}
int answer = MAX;
for(int city=0; city<n; city++) {
if((mark&(1<<city))==0) {
int newAnswer = distan[position][city] + TSP( mark|(1<<city),city);
answer = min(answer, newAnswer);
}
}
return DP[mark][position] = answer;
}
int main(){
for(int i=0; i<(1<<n); i++) {
for(int j=0; j<n; j++) {
DP[i][j] = -1;
}
}
cout << "Minimum Distance Travelled -> " << TSP(1,0);
return 0;
}
Output
Minimum Distance Travelled -> 122
public class Main {
static int n = 4;
static int[][] distan = {
{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}
};
static int completed_visit = (1 << n) - 1;
static int[][] DP = new int[32][8];
static int TSP(int mark, int position) {
if (mark == completed_visit) {
return distan[position][0];
}
if (DP[mark][position] != -1) {
return DP[mark][position];
}
int answer = Integer.MAX_VALUE;
for (int city = 0; city < n; city++) {
if ((mark & (1 << city)) == 0) {
int newAnswer = distan[position][city] + TSP(mark | (1 << city), city);
answer = Math.min(answer, newAnswer);
}
}
DP[mark][position] = answer;
return answer;
}
public static void main(String[] args) {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
DP[i][j] = -1;
}
}
System.out.println("Minimum Distance Travelled -> " + TSP(1, 0));
}
}
Output
Minimum Distance Travelled -> 122
import sys
n = 4
distan = [[0, 22, 26, 30],
[30, 0, 45, 35],
[25, 45, 0, 60],
[30, 35, 40, 0]]
completed_visit = (1 << n) - 1
DP = [[-1 for _ in range(n)] for _ in range(2 ** n)]
def TSP(mark, position):
if mark == completed_visit:
return distan[position][0]
if DP[mark][position] != -1:
return DP[mark][position]
answer = sys.maxsize
for city in range(n):
if (mark & (1 << city)) == 0:
new_answer = distan[position][city] + TSP(mark | (1 << city), city)
answer = min(answer, new_answer)
DP[mark][position] = answer
return answer
for i in range(1 << n):
for j in range(n):
DP[i][j] = -1
print("Minimum Distance Travelled ->", TSP(1, 0))
Output
Minimum Distance Travelled -> 122
