Travelling Salesman using Approximation Algorithm

We have already discussed the travelling salesperson problem using the greedy and dynamic programming approaches, and it is established that solving the travelling salesperson problems for the perfect optimal solutions is not possible in polynomial time.

Therefore, the approximation solution is expected to find a near optimal solution for this NP-Hard problem. However, an approximate algorithm is devised only if the cost function (which is defined as the distance between two plotted points) in the problem satisfies triangle inequality.

The triangle inequality is satisfied only if the cost function c, for all the vertices of a triangle u, v and w, satisfies the following equation

                 c(u, w)≤ c(u, v)+c(v, w)

It is usually automatically satisfied in many applications.

Travelling Salesperson Approximation Algorithm

The travelling salesperson approximation algorithm requires some prerequisite algorithms to be performed so we can achieve a near optimal solution. Let us look at those prerequisite algorithms briefly −

Minimum Spanning Tree − The minimum spanning tree is a tree data structure that contains all the vertices of main graph with minimum number of edges connecting them. We apply prim’s algorithm for minimum spanning tree in this case.

Pre-order Traversal − The pre-order traversal is done on tree data structures where a pointer is walked through all the nodes of the tree in a [root – left child – right child] order.

Algorithm

Step 1 − Choose any vertex of the given graph randomly as the starting and ending point.

Step 2 − Construct a minimum spanning tree of the graph with the vertex chosen as the root using prim’s algorithm.

Step 3 − Once the spanning tree is constructed, pre-order traversal is performed on the minimum spanning tree obtained in the previous step.

Step 4 − The pre-order solution obtained is the Hamiltonian path of the travelling salesperson.

Pseudocode

APPROX_TSP(G, c)
   r <- root node of the minimum spanning tree
   T <- MST_Prim(G, c, r)
   visited = {ф}
   for i in range V:
      H <- Preorder_Traversal(G)
      visited = {H}

Analysis

The approximation algorithm of the travelling salesperson problem is a 2-approximation algorithm if the triangle inequality is satisfied.

To prove this, we need to show that the approximate cost of the problem is double the optimal cost. Few observations that support this claim would be as follows −

• The cost of minimum spanning tree is never less than the cost of the optimal Hamiltonian path. That is, c(M) ≤ c(H^*).

• The cost of full walk is also twice as the cost of minimum spanning tree. A full walk is defined as the path traced while traversing the minimum spanning tree preorderly. Full walk traverses every edge present in the graph exactly twice. Thereore, c(W) = 2c(T)

• Since the preorder walk path is less than the full walk path, the output of the algorithm is always lower than the cost of the full walk.

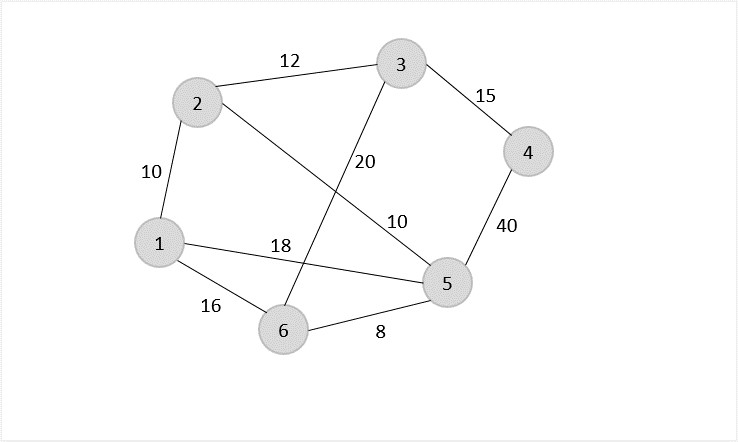
Example

Let us look at an example graph to visualize this approximation algorithm −

Solution

Consider vertex 1 from the above graph as the starting and ending point of the travelling salesperson and begin the algorithm from here.

Step 1

Starting the algorithm from vertex 1, construct a minimum spanning tree from the graph. To learn more about constructing a minimum spanning tree, please click here.

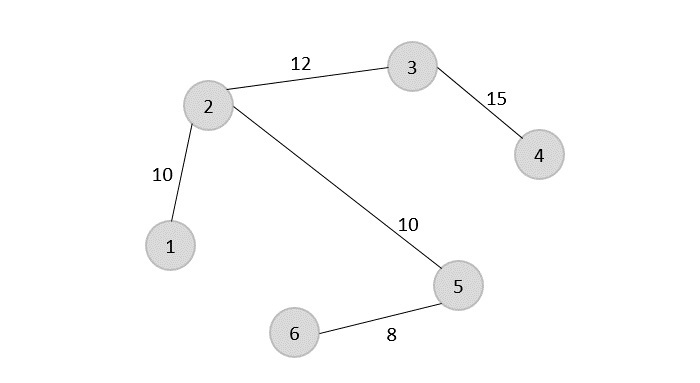
Step 2

Once, the minimum spanning tree is constructed, consider the starting vertex as the root node (i.e., vertex 1) and walk through the spanning tree preorderly.

Rotating the spanning tree for easier interpretation, we get −

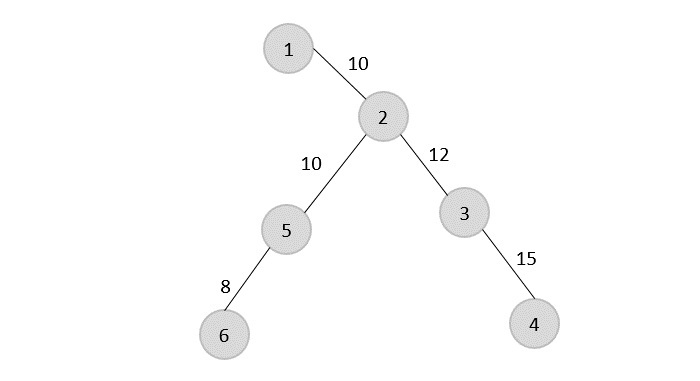
The preorder traversal of the tree is found to be − 1 → 2 → 5 → 6 → 3 → 4

Step 3

Adding the root node at the end of the traced path, we get, 1 → 2 → 5 → 6 → 3 → 4 → 1

This is the output Hamiltonian path of the travelling salesman approximation problem. The cost of the path would be the sum of all the costs in the minimum spanning tree, i.e., 55.

Implementation

Following are the implementations of the above approach in various programming langauges −

#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 6 // Number of vertices in the graph
// Function to find the minimum key vertex from the set of vertices not yet included in MST
int findMinKey(int key[], bool mstSet[]) {
   int min = INT_MAX, min_index;
   for (int v = 0; v < V; v++) {
      if (mstSet[v] == false && key[v] < min) {
         min = key[v];
         min_index = v;
      }
   }
   return min_index;
}
// Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
void primMST(int graph[V][V], int parent[]) {
   int key[V];
   bool mstSet[V];
   for (int i = 0; i < V; i++) {
      key[i] = INT_MAX;
      mstSet[i] = false;
   }
   key[0] = 0;
   parent[0] = -1;
   for (int count = 0; count < V - 1; count++) {
      int u = findMinKey(key, mstSet);
      mstSet[u] = true;
      for (int v = 0; v < V; v++) {
         if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
            parent[v] = u;
            key[v] = graph[u][v];
         }
      }
   }
}
// Function to print the preorder traversal of the Minimum Spanning Tree
void printPreorderTraversal(int parent[]) {
   printf("The preorder traversal of the tree is found to be − ");
   for (int i = 1; i < V; i++) {
      printf("%d → ", parent[i]);
   }
   printf("\n");
}
// Main function for the Traveling Salesperson Approximation Algorithm
void tspApproximation(int graph[V][V]) {
   int parent[V];
   int root = 0; // Choosing vertex 0 as the starting and ending point
   // Find the Minimum Spanning Tree using Prim's Algorithm
   primMST(graph, parent);
   // Print the preorder traversal of the Minimum Spanning Tree
   printPreorderTraversal(parent);
   // Print the Hamiltonian path (preorder traversal with the starting point added at the end)
   printf("Adding the root node at the end of the traced path ");
   for (int i = 0; i < V; i++) {
      printf("%d → ", parent[i]);
   }
   printf("%d → %d\n", root, parent[0]);
   // Calculate and print the cost of the Hamiltonian path
   int cost = 0;
   for (int i = 1; i < V; i++) {
      cost += graph[parent[i]][i];
   }
   // The cost of the path would be the sum of all the costs in the minimum spanning tree.
   printf("Sum of all the costs in the minimum spanning tree %d.\n", cost);
}
int main() {
   // Example graph represented as an adjacency matrix
   int graph[V][V] = {
      {0, 3, 1, 6, 0, 0},
      {3, 0, 5, 0, 3, 0},
      {1, 5, 0, 5, 6, 4},
      {6, 0, 5, 0, 0, 2},
      {0, 3, 6, 0, 0, 6},
      {0, 0, 4, 2, 6, 0}
   };
   tspApproximation(graph);
   return 0;
}

The preorder traversal of the tree is found to be − 0 → 0 → 5 → 1 → 2 → 
Adding the root node at the end of the traced path -1 → 0 → 0 → 5 → 1 → 2 → 0 → -1
Sum of all the costs in the minimum spanning tree 13.

#include <iostream>
#include <limits>
#define V 6 // Number of vertices in the graph
// Function to find the minimum key vertex from the set of vertices not yet included in MST
int findMinKey(int key[], bool mstSet[]) {
   int min = std::numeric_limits<int>::max();
   int min_index;
   for (int v = 0; v < V; v++) {
      if (mstSet[v] == false && key[v] < min) {
         min = key[v];
         min_index = v;
      }
   }
   return min_index;
}
// Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
void primMST(int graph[V][V], int parent[]) {
   int key[V];
   bool mstSet[V];
   for (int i = 0; i < V; i++) {
      key[i] = std::numeric_limits<int>::max();
      mstSet[i] = false;
   }
   key[0] = 0;
   parent[0] = -1;
   for (int count = 0; count < V - 1; count++) {
      int u = findMinKey(key, mstSet);
      mstSet[u] = true;
      for (int v = 0; v < V; v++) {
         if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
            parent[v] = u;
            key[v] = graph[u][v];
         }
      }
   }
}
// Function to print the preorder traversal of the Minimum Spanning Tree
void printPreorderTraversal(int parent[]) {
   std::cout << "The preorder traversal of the tree is found to be − ";
   for (int i = 1; i < V; i++) {
      std::cout << parent[i] << " → ";
   }
   std::cout << std::endl;
}
// Main function for the Traveling Salesperson Approximation Algorithm
void tspApproximation(int graph[V][V]) {
   int parent[V];
   int root = 0; // Choosing vertex 0 as the starting and ending point
   // Find the Minimum Spanning Tree using Prim's Algorithm
   primMST(graph, parent);
   // Print the preorder traversal of the Minimum Spanning Tree
   printPreorderTraversal(parent);
   // Print the Hamiltonian path (preorder traversal with the starting point added at the end)
   std::cout << "Adding the root node at the end of the traced path ";
   for (int i = 0; i < V; i++) {
      std::cout << parent[i] << " → ";
   }
   std::cout << root << " → " << parent[0] << std::endl;
   // Calculate and print the cost of the Hamiltonian path
   int cost = 0;
   for (int i = 1; i < V; i++) {
      cost += graph[parent[i]][i];
   }
   // The cost of the path would be the sum of all the costs in the minimum spanning tree.
   std::cout << "Sum of all the costs in the minimum spanning tree: " << cost << "." << std::endl;
}
int main() {
   // Example graph represented as an adjacency matrix
   int graph[V][V] = {
      {0, 3, 1, 6, 0, 0},
      {3, 0, 5, 0, 3, 0},
      {1, 5, 0, 5, 6, 4},
      {6, 0, 5, 0, 0, 2},
      {0, 3, 6, 0, 0, 6},
      {0, 0, 4, 2, 6, 0}
   };
   tspApproximation(graph);
   return 0;
}

The preorder traversal of the tree is found to be − 0 → 0 → 5 → 1 → 2 → 
Adding the root node at the end of the traced path -1 → 0 → 0 → 5 → 1 → 2 → 0 → -1
Sum of all the costs in the minimum spanning tree: 13.

import java.util.Arrays;
public class TravelingSalesperson {
   static final int V = 6; // Number of vertices in the graph
   // Function to find the minimum key vertex from the set of vertices not yet included in MST
   static int findMinKey(int key[], boolean mstSet[]) {
      int min = Integer.MAX_VALUE;
      int minIndex = -1;
      for (int v = 0; v < V; v++) {
         if (!mstSet[v] && key[v] < min) {
            min = key[v];
            minIndex = v;
         }
      }
      return minIndex;
   }
   // Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
   static void primMST(int graph[][], int parent[]) {
      int key[] = new int[V];
      boolean mstSet[] = new boolean[V];
      Arrays.fill(key, Integer.MAX_VALUE);
      Arrays.fill(mstSet, false);
      key[0] = 0;
      parent[0] = -1;
      for (int count = 0; count < V - 1; count++) {
         int u = findMinKey(key, mstSet);
         mstSet[u] = true;
         for (int v = 0; v < V; v++) {
            if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
               parent[v] = u;
               key[v] = graph[u][v];
            }
         }
      }
   }
   // Function to print the preorder traversal of the Minimum Spanning Tree
   static void printPreorderTraversal(int parent[]) {
      System.out.print("The preorder traversal of the tree is found to be  ");
      for (int i = 1; i < V; i++) {
         System.out.print(parent[i] + " -> ");
      }
      System.out.println();
   }
   // Main function for the Traveling Salesperson Approximation Algorithm
   static void tspApproximation(int graph[][]) {
      int parent[] = new int[V];
      int root = 0; // Choosing vertex 0 as the starting and ending point
      // Find the Minimum Spanning Tree using Prim's Algorithm
      primMST(graph, parent);
      // Print the preorder traversal of the Minimum Spanning Tree
      printPreorderTraversal(parent);
      // Print the Hamiltonian path (preorder traversal with the starting point added at the end)
      System.out.print("Adding the root node at the end of the traced path ");
      for (int i = 0; i < V; i++) {
         System.out.print(parent[i] + " -> ");
      }
      System.out.println(root + "  " + parent[0]);
      // Calculate and print the cost of the Hamiltonian path
      int cost = 0;
      for (int i = 1; i < V; i++) {
         cost += graph[parent[i]][i];
      }
      // The cost of the path would be the sum of all the costs in the minimum spanning tree.
      System.out.println("Sum of all the costs in the minimum spanning tree: " + cost);
   }
   public static void main(String[] args) {
      // Example graph represented as an adjacency matrix
      int graph[][] = {
         {0, 3, 1, 6, 0, 0},
         {3, 0, 5, 0, 3, 0},
         {1, 5, 0, 5, 6, 4},
         {6, 0, 5, 0, 0, 2},
         {0, 3, 6, 0, 0, 6},
         {0, 0, 4, 2, 6, 0}
      };
      tspApproximation(graph);
   }
}

The preorder traversal of the tree is found to be  0 -> 0 -> 5 -> 1 -> 2 -> 
Adding the root node at the end of the traced path -1 -> 0 -> 0 -> 5 -> 1 -> 2 -> 0  -1
Sum of all the costs in the minimum spanning tree: 13

import sys
V = 6  # Number of vertices in the graph
# Function to find the minimum key vertex from the set of vertices not yet included in MST
def findMinKey(key, mstSet):
    min_val = sys.maxsize
    min_index = -1
    for v in range(V):
        if not mstSet[v] and key[v] < min_val:
            min_val = key[v]
            min_index = v
    return min_index
# Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
def primMST(graph, parent):
    key = [sys.maxsize] * V
    mstSet = [False] * V
    key[0] = 0
    parent[0] = -1
    for _ in range(V - 1):
        u = findMinKey(key, mstSet)
        mstSet[u] = True
        for v in range(V):
            if graph[u][v] and not mstSet[v] and graph[u][v] < key[v]:
                parent[v] = u
                key[v] = graph[u][v]
# Function to print the preorder traversal of the Minimum Spanning Tree
def printPreorderTraversal(parent):
    print("The preorder traversal of the tree is found to be − ", end="")
    for i in range(1, V):
        print(parent[i], " → ", end="")
    print()
# Main function for the Traveling Salesperson Approximation Algorithm
def tspApproximation(graph):
    parent = [0] * V
    root = 0  # Choosing vertex 0 as the starting and ending point
    # Find the Minimum Spanning Tree using Prim's Algorithm
    primMST(graph, parent)
    # Print the preorder traversal of the Minimum Spanning Tree
    printPreorderTraversal(parent)
    # Print the Hamiltonian path (preorder traversal with the starting point added at the end)
    print("Adding the root node at the end of the traced path ", end="")
    for i in range(V):
        print(parent[i], " → ", end="")
    print(root, " → ", parent[0])
    # Calculate and print the cost of the Hamiltonian path
    cost = 0
    for i in range(1, V):
        cost += graph[parent[i]][i]
    # The cost of the path would be the sum of all the costs in the minimum spanning tree.
    print("Sum of all the costs in the minimum spanning tree:", cost)
if __name__ == "__main__":
    # Example graph represented as an adjacency matrix
    graph = [
        [0, 3, 1, 6, 0, 0],
        [3, 0, 5, 0, 3, 0],
        [1, 5, 0, 5, 6, 4],
        [6, 0, 5, 0, 0, 2],
        [0, 3, 6, 0, 0, 6],
        [0, 0, 4, 2, 6, 0]
    ]
    tspApproximation(graph)

The preorder traversal of the tree is found to be − 0  → 0  → 5  → 1  → 2  → 
Adding the root node at the end of the traced path -1  → 0  → 0  → 5  → 1  → 2  → 0  →  -1
Sum of all the costs in the minimum spanning tree: 13