Design and Analysis - Shell Sort

Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.

This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth's formula as −

h = h * 3 + 1
where −
   h is interval with initial value 1

This algorithm is quite efficient for medium-sized data sets as its average and worst case complexity are of O(n), where n is the number of items.

Shell Sort Algorithm

Following is the algorithm for shell sort.

Step 1 − Initialize the value of h

Step 2 − Divide the list into smaller sub-list of equal interval h

Step 3 − Sort these sub-lists using insertion sort

Step 3 − Repeat until complete list is sorted

Pseudocode

Following is the pseudocode for shell sort.

procedure shellSort()
   A : array of items

   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1
   end while

   while interval > 0 do:
      for outer = interval; outer < A.length; outer ++ do:

         /* select value to be inserted */
         valueToInsert = A[outer]
         inner = outer;
            
            /*shift element towards right*/
            while inner > interval -1 &&  A[inner - interval] >= valueToInsert do:
               A[inner] = A[inner - interval]
               inner = inner – interval
            end while
         
         /* insert the number at hole position */
         A[inner] = valueToInsert
         end for
   
   /* calculate interval*/
   interval = (interval -1) /3;
   end while
end procedure

Example

Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 14}

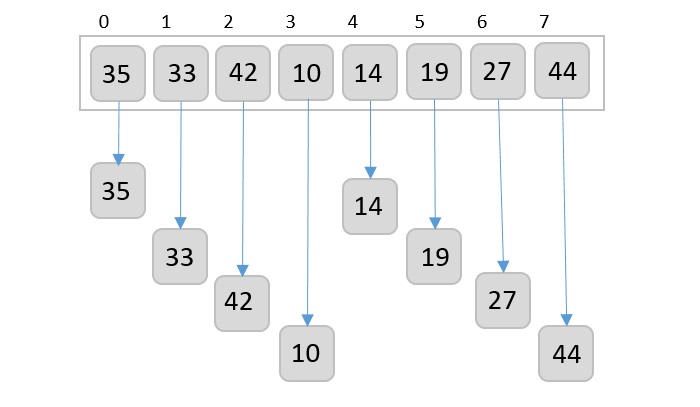
We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this −

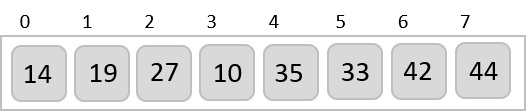
Then, we take interval of 2 and this gap generates two sub-lists - {14, 27, 35, 42}, {19, 10, 33, 44}

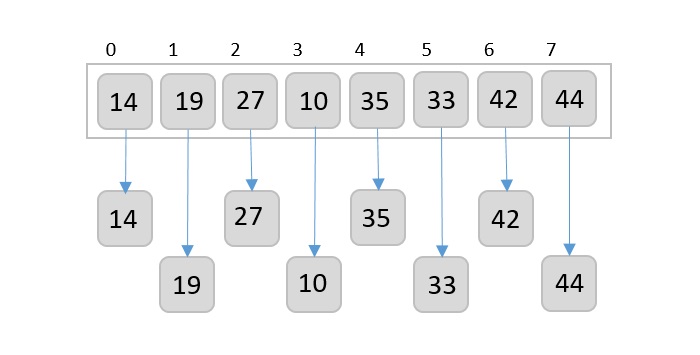
We compare and swap the values, if required, in the original array. After this step, the array should look like this −

Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.

Following is the step-by-step depiction −

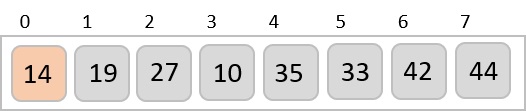
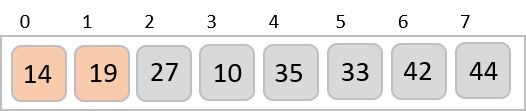
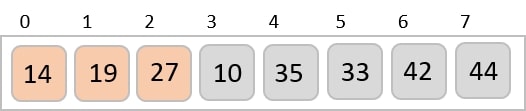
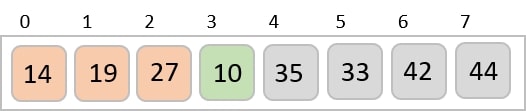
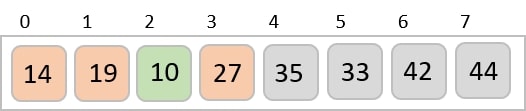
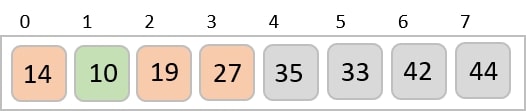
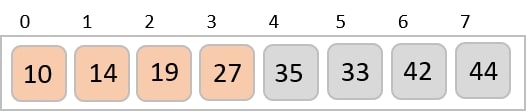
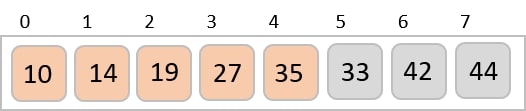
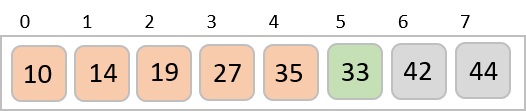
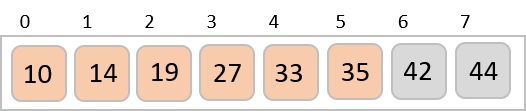
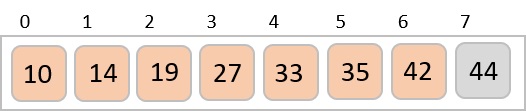
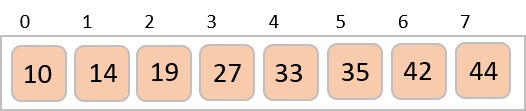
We see that it required only four swaps to sort the rest of the array.

Example

Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.

#include <stdio.h>
void shellSort(int arr[], int n){
   int gap, j, k;
   for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
      for(j = gap; j<n; j++) {
         for(k = j-gap; k>=0; k -= gap) {
            if(arr[k+gap] >= arr[k])
               break;
            else {
               int temp;
               temp = arr[k+gap];
               arr[k+gap] = arr[k];
               arr[k] = temp;
            }
         }
      }
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   shellSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 33 45 62 12 98
Array after Sorting: 12 33 45 62 98

#include<iostream>
using namespace std;
void shellSort(int *arr, int n){
   int gap, j, k;
   for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
      for(j = gap; j<n; j++) {
         for(k = j-gap; k>=0; k -= gap) {
            if(arr[k+gap] >= arr[k])
               break;
            else {
               int temp;
               temp = arr[k+gap];
               arr[k+gap] = arr[k];
               arr[k] = temp;
            }
         }
      }
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   shellSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 33 45 62 12 98
Array after Sorting: 12 33 45 62 98

import java.io.*;
import java.util.*;
public class ShellSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {33, 45, 62, 12, 98}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      int gap;
      for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
         for(int j = gap; j<n; j++) {
            for(int k = j-gap; k>=0; k -= gap) {
               if(arr[k+gap] >= arr[k])
                  break;
               else {
                  int temp;
                  temp = arr[k+gap];
                  arr[k+gap] = arr[k];
                  arr[k] = temp;
               }
            }
         }
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 33 45 62 12 98
Array After Sorting: 12 33 45 62 98

def shell_sort(array,n):
   gap = n//2 #using floor division to avoid float values as result
   while gap > 0:
      for i in range(int(gap),n):
         temp = array[i]
         j = i
         while j >= gap and array[j-gap] >temp:
            array[j] = array[j-gap]
            j -= gap
            array[j] = temp
      gap = gap // 2 #using floor division to avoid float values as result

arr = [33, 45, 62, 12, 98]
n = len(arr)
print("Array before Sorting: ")
print(arr)
shell_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[33, 45, 62, 12, 98]
Array after Sorting: 
[12, 33, 45, 62, 98]

Kickstart Your Career

Get certified by completing the course

Get Started