MATLAB - Inverse Fourier Transform

Quiz

The Inverse Fourier Transform in MATLAB is a function that takes a frequency-domain representation of a signal and converts it back to the time-domain representation. It is the reverse process of the Fourier Transform, which converts a time-domain signal into its frequency-domain representation.

In MATLAB, the Inverse Fourier Transform is computed using the ifft function for one-dimensional signals and the ifft2 function for two-dimensional signals. The result of the Inverse Fourier Transform is a signal that represents the original time-domain signal.

The Inverse Fourier Transform is useful in signal processing, image processing, and communications, where it is used to analyze and manipulate signals in the frequency domain. It allows for operations such as filtering, compression, and modulation to be performed on signals represented in the frequency domain.

Inverse Fourier Transform Using ifft()

The ifft() function in MATLAB computes the Inverse Discrete Fourier Transform (IDFT) of a sequence. It takes a 1D or 2D array representing the frequency-domain signal (obtained, for example, using the fft() function) and returns the corresponding time-domain signal.

The Inverse Discrete Fourier Transform is the reverse process of the Discrete Fourier Transform (DFT). It converts a frequency-domain representation of a signal back to the time-domain representation. This is useful in applications where signals need to be analyzed or manipulated in the frequency domain and then converted back to the time domain for further processing or interpretation.

Syntax

X = ifft(Y)
X = ifft(Y,n)
X = ifft(Y,n,dim)
X = ifft(___,symflag)

Syntax Explanation

X = ifft(Y) Calculates the inverse Fourier transform of Y using a fast algorithm. The result X has the same size as Y.

If Y is a vector, ifft(Y) returns the inverse transform of the vector.
If Y is a matrix, ifft(Y) returns the inverse transform of each column of the matrix.
If Y is a multidimensional array, ifft(Y) treats the values along the first non-singleton dimension as vectors and returns the inverse transform of each vector.

X = ifft(Y,n) − Calculates the inverse Fourier transform of Y, but it pads Y with zeros to make its length n before performing the transform.

X = ifft(Y,n,dim) − Calculates the inverse Fourier transform of Y along the specified dimension dim, padding with zeros to make the length n along that dimension. For instance, if Y is a matrix, ifft(Y,n,2) computes the n-point inverse transform for each row.

X = ifft(___,symflag) − Lets you specify the symmetry of Y along with any of the previous input argument combinations. For instance, ifft(Y,'symmetric') treats Y as conjugate symmetric.

Examples of Inverse Fourier Transform in MATLAB

Let us see examples for each of the syntax we mentioned above.

Example 1: Calculating Inverse Fourier Transform using ifft(Y)

The code we have is as follows −

% Generate a signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = sin(2*pi*f*t);

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform
X = ifft(Y);

% Plot the original and reconstructed signals
subplot(2,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, real(X)); % Display real part of X
title('Reconstructed Signal');
xlabel('Time');
ylabel('Amplitude');

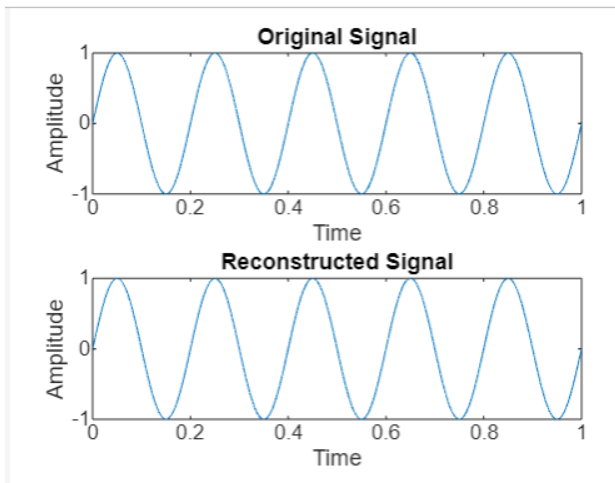
In this example −

We first generate a sinusoidal signal signal.
We then compute the Fourier Transform of the signal using fft(), resulting in Y.
Next, we use ifft(Y) to calculate the Inverse Fourier Transform, which should ideally reconstruct the original signal.
Finally, we plot the original signal and the reconstructed signal to compare them.

When the code is executed the output we get is −

Example 2: Calculating Inverse Fourier Transform with Zero Padding

The code we have is as follows −

% Generate a signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = sin(2*pi*f*t);

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform with zero padding
n = 2000; % Length to pad
X = ifft(Y, n);

% Plot the original and padded signals
subplot(2,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
t_padded = linspace(0, 1, n); % Time vector for padded signal
plot(t_padded, real(X)); % Display real part of X
title('Padded Signal');
xlabel('Time');
ylabel('Amplitude');

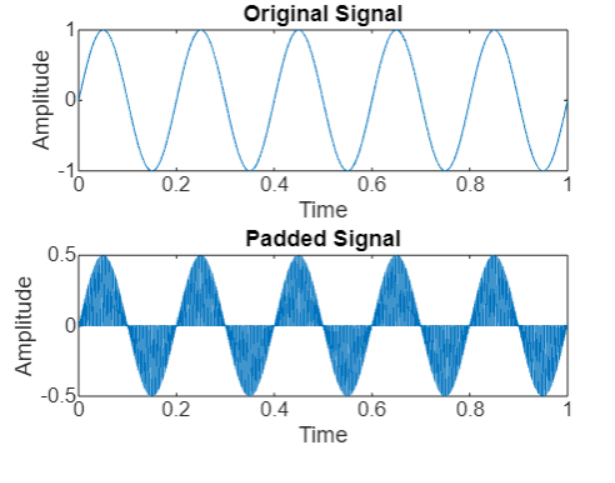
This example is similar to the previous one but with the addition of zero padding.

After computing the Fourier Transform of the signal, we use ifft(Y, n) to calculate the Inverse Fourier Transform with zero padding to a length of n.
Zero padding can be useful for increasing the resolution of the frequency domain representation of a signal.

The output on execution is −

Example 3

Calculating Inverse Fourier Transform along a Specific Dimension with Zero Padding

The code we have is −

% Create a 2D matrix
A = magic(4); % Magic square matrix
disp('Original Matrix:');
disp(A);

% Compute the Fourier Transform along the columns
Y = fft(A, [], 2);

% Compute the Inverse Fourier Transform along the columns with zero padding
n = 8; % Length to pad
X = ifft(Y, n, 2);

% Display the original and padded matrices
disp('Original Matrix after IFFT along columns with zero padding:');
disp(X);

In this example,

We start with a 4x4 magic square matrix A.
We then compute the Fourier Transform of A along the columns using fft(A, [], 2), resulting in Y.
Next, we use ifft(Y, n, 2) to calculate the Inverse Fourier Transform along the columns with zero padding to a length of n.
The result X is a 4x8 matrix where each row is the n-point inverse transform of the corresponding row in the original matrix A.

The output on execution is as follows −

>> % Create a 2D matrix
A = magic(4); % Magic square matrix
disp('Original Matrix:');
disp(A);

% Compute the Fourier Transform along the columns
Y = fft(A, [], 2);

% Compute the Inverse Fourier Transform along the columns with zero padding
n = 8; % Length to pad
X = ifft(Y, n, 2);

% Display the original and padded matrices
disp('Original Matrix after IFFT along columns with zero padding:');
disp(X);

Original Matrix:
   16    2    3   13
    5   11   10    8
    9    7    6   12
    4   14   15    1
Original Matrix after IFFT along columns with zero padding:
 Columns 1 through 4:

   8.0000 +      0i   4.2500 + 4.7426i   1.0000 +      0i   4.2500 - 0.1464i
   2.5000 +      0i   4.2500 - 1.9142i   5.5000 +      0i   4.2500 + 0.1464i
   4.5000 +      0i   4.2500 + 0.9142i   3.5000 +      0i   4.2500 + 0.1464i
   2.0000 +      0i   4.2500 - 3.7426i   7.0000 +      0i   4.2500 - 0.1464i

 Columns 5 through 8:

   1.5000 +      0i   4.2500 - 3.7426i   6.5000 +      0i   4.2500 - 0.8536i
   5.0000 +      0i   4.2500 + 0.9142i   4.0000 +      0i   4.2500 + 0.8536i
   3.0000 +      0i   4.2500 - 1.9142i   6.0000 +      0i   4.2500 + 0.8536i
   7.5000 +      0i   4.2500 + 4.7426i   0.5000 +      0i   4.2500 - 0.8536i

>>

Example 4: Calculating Inverse Fourier Transform with Specified Symmetry

The code we have is as follows −

% Create a complex signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = exp(1i*2*pi*f*t); % Complex exponential signal

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform with symmetric treatment
X = ifft(Y, 'symmetric');

% Plot the real part of the original and reconstructed signals
subplot(2,1,1);
plot(t, real(signal));
title('Original Signal (Real Part)');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, real(X)); % Display real part of X
title('Reconstructed Signal (Real Part)');
xlabel('Time');
ylabel('Amplitude');

In this example we have the ifft function with the 'symmetric' flag to specify the symmetry of the input signal.
We first create a complex exponential signal signal and compute its Fourier Transform.
By using ifft(Y, 'symmetric'), we calculate the Inverse Fourier Transform with symmetric treatment, which assumes that the input signal is conjugate symmetric.
The real part of the original and reconstructed signals is plotted for comparison.

The output we get on execution is as follows −

2-D Inverse Fourier Transform using ifft2()

The 2-D Inverse Fourier Transform using ifft2() is a MATLAB function that calculates the inverse Fourier transform of a 2-D matrix. It is the inverse operation of the 2-D Fourier Transform, converting a frequency-domain representation of an image back to the spatial domain.

This function is particularly useful in image processing for tasks such as image reconstruction, filtering, and restoration. It takes a 2-D matrix representing the frequency-domain image and returns the corresponding spatial-domain image.

Syntax

X = ifft2(Y)
X = ifft2(Y,m,n)
X = ifft2(___,symflag)

Syntax explanation

X = ifft2(Y) − Calculates the 2D Inverse Fourier Transform of a matrix Y using a fast algorithm. If Y is a multidimensional array, ifft2 computes the 2D inverse transform for each dimension higher than 2. The output X has the same size as Y.

X = ifft2(Y,m,n) − Adjusts the size of Y to an m-by-n matrix by either truncating or padding Y with zeros before computing the inverse transform. The output X is also m-by-n. If Y is a multidimensional array, ifft2 reshapes the first two dimensions of Y to match m and n.

X = ifft2(___,symflag) − Lets you specify the symmetry of Y in addition to any of the previous input argument combinations. For instance, ifft2(Y,'symmetric') treats Y as conjugate symmetric.

Let us work on a few examples based on the syntax we mentioned above.

Example 1: Calculating 2D Inverse Fourier Transform

The code we have is as follows −

% Compute the 2D Fourier Transform
Y = fft2(A);

% Compute the Inverse Fourier Transform
X = ifft2(Y);

% Display the original and reconstructed matrices
disp('Original Matrix:');
disp(A);

disp('Reconstructed Matrix:');
disp(X);

This example demonstrates the use of ifft2() to calculate the 2D Inverse Fourier Transform of a matrix Y.
We start with a simple 3x3 matrix A.
We then compute the 2D Fourier Transform of A using fft2(), resulting in Y.
Finally, we use ifft2(Y) to calculate the Inverse Fourier Transform, which should ideally reconstruct the original matrix A.
The original and reconstructed matrices are displayed for comparison.

On execution we get −

Original Matrix:
     1     2     3
     4     5     6
     7     8     9

Reconstructed Matrix:
     1     2     3
     4     5     6
     7     8     9

Example 2: Adjusting Size for 2D Inverse Fourier Transform

The code we have is as follows −

% Create a simple 3x3 matrix
A = [1 2 3; 4 5 6; 7 8 9];

% Compute the 2D Fourier Transform
Y = fft2(A);

% Adjust the size and compute the Inverse Fourier Transform
m = 4; % Desired number of rows
n = 5; % Desired number of columns
X = ifft2(Y, m, n);

% Display the original and adjusted-size matrices
disp('Original Matrix:');
disp(A);

disp('Adjusted-size Matrix:');
disp(X);

This example illustrates the use of ifft2(Y,m,n) to adjust the size of the 2D matrix Y before computing the inverse transform.
We start with a simple 3x3 matrix A.
We compute the 2D Fourier Transform of A using fft2(), resulting in Y.
We then use ifft2(Y, m, n) to adjust the size of Y to a 4x5 matrix by padding with zeros, and compute the Inverse Fourier Transform, resulting in X.
The original and adjusted-size matrices are displayed for comparison.

On execution we get following output −

Original Matrix:
   1   2   3
   4   5   6
   7   8   9
Adjusted-size Matrix:
 Columns 1 through 4:

   0.4500 +      0i   0.9653 - 0.2010i   0.8126 - 0.0635i   1.2124 - 0.2270i
   2.0853 - 0.2853i   2.6006 - 0.4863i   2.4479 - 0.3488i   2.8477 - 0.5123i
   1.8000 - 0.7794i   2.3153 - 0.9804i   2.1626 - 0.8429i   2.5624 - 1.0064i
   2.8647 + 1.0647i   3.3800 + 0.8637i   3.2273 + 1.0012i   3.6271 + 0.8377i

 Column 5:

   1.0597 + 0.4915i
   2.6950 + 0.2062i
   2.4097 - 0.2879i
   3.4744 + 1.5562i

Example 3: Specifying Symmetry for 2D Inverse Fourier Transform

The code we have is as follows −

% Create a 2D matrix with complex values
A = [1+2i, 3-1i, 5+4i; -2+1i, 6-3i, 8+7i; 9-2i, 4+5i, -1-6i];

% Compute the 2D Fourier Transform
Y = fft2(A);

% Compute the Inverse Fourier Transform with symmetric treatment
X = ifft2(Y, 'symmetric');

% Display the original and reconstructed matrices
disp('Original Matrix:');
disp(A);

disp('Reconstructed Matrix:');
disp(X);

This example demonstrates the use of ifft2(___,symflag) to specify the symmetry of the input matrix Y before computing the inverse transform.
We start with a 3x3 matrix A containing complex values.
We compute the 2D Fourier Transform of A using fft2(), resulting in Y.
By using ifft2(Y, 'symmetric'), we compute the Inverse Fourier Transform of Y with symmetric treatment, which assumes Y is conjugate symmetric.
The original and reconstructed matrices are displayed for comparison.

On execution the output we get is −

Original Matrix:
   1.0000 + 2.0000i   3.0000 - 1.0000i   5.0000 + 4.0000i
  -2.0000 + 1.0000i   6.0000 - 3.0000i   8.0000 + 7.0000i
   9.0000 - 2.0000i   4.0000 + 5.0000i  -1.0000 - 6.0000i

Reconstructed Matrix:
   -0.3472    5.6943    8.2717
   -9.3131    7.9245    8.7698
   15.3509    1.6906   -5.0415

Print Page