
- Aptitude Test Preparation
- Aptitude - Home
- Aptitude - Overview
- Quantitative Aptitude
- Aptitude Useful Resources
- Aptitude - Questions & Answers
Aptitude - Geometry
Point
A point is an exact location
Line Segment
The straight path between two points A and B is called a line segment AB. A line segment has two end points.

Ray
On extending a line segment AB indefinitely in one direction we get the ray AB. Ray AB has one end point, namely A.

LINE
A line segment AB extended indefinitely in both directions is called line AB.

A line contains infinitely many points.
Through a given points , infinitaly many lines can be drawn.
One and only one line can be drawn to pass through two given points A and B.
Two line meet in a point.
Two planes meet in a line.
Collinear
In the given figure, the points A,B,C are collinear.
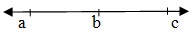
Concurrent Lines
Three or more lines intersecting at the same points are called concurrent lines.
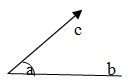
Angle
Two rays OA and OB having a common end points O form angle AOB, written as ∠AOB
Measure of an Angle
The amount of turning from OA to OB is called the measure of ∠AOB written as m(∠AOB).
An angle of 360°
If a ray OA starting from its original position OA , rotates about O in anticlockwise direction and after a complete rotation comes back to its original position , then we say that it has rotated through 360. This complete rotation is divided into 360° equal parts. Then, each part is called 1 degree , written as 1°
1° = 60 minutes, written as 60'
1 minute = 60 seconds, written as 60"
Types of Angle
Right angle - An angle whose measure is 90° is called a right angle.
Acute angle - An angle whose measure is less than 90° is called an acute angle.
Obtuse angle - An angle whose measure is more than 90° but less than 180°, is called an obtues angle.
Straight angle - An angle whose measure is 180° is called a Straight angle.
Reflex angle - An angle whose measure is more than 180° but less than 360°, is called a Reflex angle.
Complete angle - An angle whose measure is 360°, is called a complete angle.
Equal angle - Two angles are said to be equal , if they have the same measure.
Complementary angleTwo angles are said to be complementary if the sum of their measures is 90. For example, angles measuring 65° and 25° are complementary angle.
Supplementary angle - Two angle are said to be supplementary if the sum of their measures is 180°. For example, angles measures 70° and 110° are supplementary.
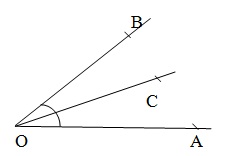
Adjacent angle - Two angles are called adjacent angle if they have the same vertex and a common arm such that non-common arms are on either side of the comman arm. In the given figure , ∠AOC and ∠BOC are adjacent angle.
Important Results
If a ray stands on a line , than the sum of two adjacent angle so formed is 180° In the given figure , ray CP stands on line AB.
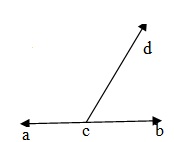
∴ ∠ACD + ∠BCD = 180°.
The sum of all angle formed on the same side of a line at a given point on the line is 180°. In the given figure four angle are formed on the same side of AOB.
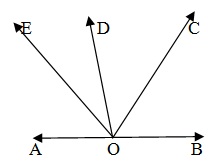
∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.
The sum of all angle around a point is 360° In the given figure five angle are formed around a point O.
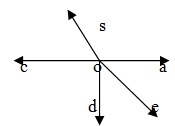
∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
Vertically Opposite Angles
If two lines A Band CD intersect at a point O, then AOC , BOD and BOC , AOD are two pair of vertically opposites angle Vertically opposite angle are always equal.
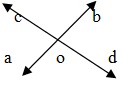
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
Parallel Lines
If two lines lie in the same plane and do not intersect when produced on either side then such lines are said to be paralleled and we write , L||m.
Traversal line cutting parallel lines
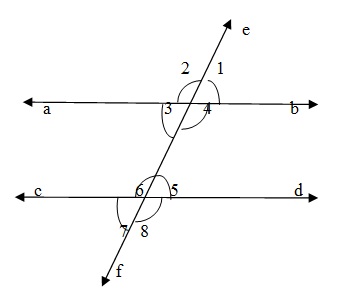
Let two parallel lines AB and CD be cut by a transversal EF. Then
Corresponding angle are equal
(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)
Alternate interior angles are equal.
(∠3 =∠5 ) and (∠4 =∠6 )
Consective interior angles are supplementary
∠4+∠5 = 180° and ∠3 +∠6 = 180°.
Triangle
A figure bounded by three straight lines is called a triangle. In the given figure , we have ∆ABC; ∆ABC having three vertices A,B,C. In has three angles, namely ∠A,∠B and ∠C. It has three sides , namely AB, AC and BC.
Types of Triangle
A triangle having all sides equal is called an equilateral triangle.
A triangle having two sides equal, is called an isosceles triangle.
A triangle having all sides of different lengths,is called a scalene triangle.
A triangle one of whose angles measures 90°,is called a right triangle.
A triangle one of whose angle lies between 90° and 180° is called an obtuse triangle.
A triangle each of whose angle is acute, is called an acute triangle.
The sum of all sides of a triangle is called the perimeter of the triangle.
The sum of two sides of a triangle is greater than the third side.
In a right angled ABC in which ∠B = 90°, we have AC2 =AB2+BC2. This is called Pythagoras Theorem.
Quadrilateral
A figure bounded by four straight line is called a quadrilateral. The sum of all angles of a quadrilateral is 360°.
Rectangle - A quadrilateral is called a rectangle, if its opposite side are equal and each of its angle is 90°. In given fig. ABCD is a rectangle.
Square - A quadrilateral is called a square, if all of its sides are equal and each of its angles measures 90°. In given fig. ABCD is square in which AB = BC = CD = DA.
Parallelogram - A quadrilateral is called a parallelogram, if its opposite sides are parallel. In given fig. ABCD is a parallelogram in which AB = DC & AD = BC.
Rhombus - A parallelogram having all sides equal is called a rhombus. In given fig. ABCD is a rhombus in which AB =BC =CD=DA, AB || DC and AD || BC.
Important Facts
A quadrilateral is a rectangle if opposite sides are equal and its diagonals are equal.
A quadrilateral is a Square if all sides are equal and the diagonal are equal.
A quadrilateral is a parallelogram, if opposite sides are equal.
A quadrilateral is a parallelogram but not a rectangle, if opposite sides are equal but the diagonals are not equal.
A quadrilateral is a rhombus but not a square if all their sides are equal and the diagonals are not equal.
Results on Quadrilateral
In a parallelogram, we have
Opposite sides are equal.
Opposite angles are equal.
Each diagonal bisects the parallelogram.
Diagonals of a parallelogram bisect each other.
Diagonals of a rectangle are equal.
Diagonals of a rhombus bisect each other at right angles.
Results on Circle
The perpendicular from the center to a chord bisects the chord.
There is one and only one circle passing through three non collinear points.
Angle in a semi circle is a right angle.
Opposite angles of a cyclic quadrilateral are supplementary.
Angle in the same segment of a circle is equal.
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Two tangent to a circle from a point outside it are equal.
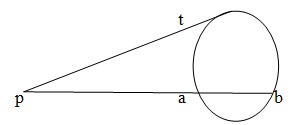
If PT is a tangent to a circle and PAB is a secant, Then PA x PB= PT2