Aptitude - Co-ordinate Geometry

---

---

Position of a point in a plane

In coordinate geometry, points are placed on the "coordinate plane" as shown below. It has two scales - one running across the plane called the "x axis" and another right angle to it called the y axis. (These can be thought of as similar to the column and row in the paragraph above.) The point where the axes cross is called the origin and is where both x and y are zero.

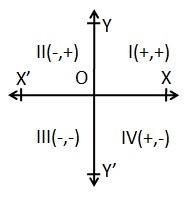
On the x-axis, values to the right are positive and those to the left are negative. On the y-axis, values above the origin are positive and those below are negative. A point's location on the plane is given by two numbers; the first tells where it is on the x-axis and the second which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates".

Note that the order is important; the x coordinate is always the first one of the pair.

Distance between two points

If A(x₁,y₁) and B (x₂,y₂) be two points, then

AB =√(x2-x1)2 + (y2-y1)2

Distance of a point from the origin

The distance of a points A(x, y) from the origin O(0, 0) is given by

OA =√(x2+y2)

Area of a triangle

If A(x₁,y₁), B(x₂,y₂) and C= (X₃, Y₃)be three vertices of a ∆ABC, then its area is given by:

∆ = 1/2 {x1(y2- Y3)+ x2(Y3- Y1) +X3(y1-y2)}

Condition of co linearity of three points

Three points A(x₁,y₁), B(x₂,y₂) and C= (X₃, Y₃) are collinear if and only if ar(√ABC)= 0.

∴ A, B, C are collinear ⇒ x₁(y₂- Y₃)+ x₂(Y₃- Y₁) +X₃(y₁-y₂) = 0

Division of a line segment by a point

If a point p(x,y) divides the join of A(x₁,y₁) and B(x₂,y₂) in the ratio m:n, then

X= (mx2+nx1)/m+n and Y =(my2+ny1)/m+n

If A(x₁,y₁) and B(x₂,y₂) be the end points of a line segment AB, then the co-ordinates of midpoint of AB are

[(x1 + x2)/ 2 , (y1 + y2)/ 2]

Centroid of a triangle

The point of intersection of all the medians of a triangle is called its centroid. If A(x₁,y₁), B(x₂,y₂) and C= (X₃, Y₃) be the vertices of ABC, then the co-ordinates of its centroid are { (1/3 (x₁+x₂+x₃),1/3 (y₁+y₂+Y₃)}

Various types of Quadrilaterals

A quadrilateral is

• A rectangle if its opposite sides is equal and diagonals are equal.

• A parallelogram but not a rectangle, if it's opposite sides are equal and the diagonals are not equal.

• A square, if all sides are equal and diagonal are equal.

• A rhombus but not a square, if all sides are equal and diagonals are not equal.

Equations of lines

• The equation of x-axis is y =0.

• The equation of y –axis is x = 0.

• The equation of a line parallel to y-axis at a distance a from it, is x= a.

• The equation of a line parallel to x-axis at a distance b from it, is y= b.

• The equation of a line passing through the points A(x₁,y₁) and B(x₂,y₂) is y-y₁/ x-x₁ = y₂-y₁/x₂-x₁. Slop of such a line is y₂-y₁/x₂-x₁.

• The equation of a line in slop intercept form is Y= mx+ c, where m is its slope.

Solved Examples

Solved Examples