- Aptitude Test Preparation
- Aptitude - Home
- Aptitude - Overview
- Quantitative Aptitude
- Aptitude Useful Resources
- Aptitude - Questions & Answers
Geometry - Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Geometry. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

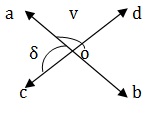
Q 1 - In the given figure, straight line AB and CD intersect at O. IF ∠δ =3∠v, then ∠v = ?
Answer : B
Explanation
COD is a straight line ∴ ∠δ + ∠v =180⁰ ⇒ 3v +v =180 ⇒ 4v = 180 ⇒ v =45⁰.
Q 2 - Two lines intersect
Answer : A
Explanation
Two lines intersect at a point.
Answer : B
Explanation
∠B = ∠A = 65⁰ (corr. ∠s). ∴ ∠B +∠C= 180⁰ ⇒ 65⁰ +∠C = 180⁰ ⇒ ∠C = ( 180⁰ - 65⁰) = 115⁰.
Answer : A
Explanation
(∠A+∠B) +(∠B+∠C) =(65⁰+140⁰)= 205⁰ ⇒ (∠A+∠B+∠C) +∠B =205⁰ ⇒ 180⁰ +∠B=205⁰ ⇒ ∠B =(205-180)⁰ =25⁰
Q 5 - The angle of a triangle are 3x⁰, (2x-7)⁰ and (4x-11)⁰. The value of x is :
Answer : A
Explanation
The sum of the angle of a triangle is 180⁰. ∴ 3x = 2x - 7 + 4x -11 = 180 ⇒ 9x =162 ⇒ x = 18. Hence, x = 18.
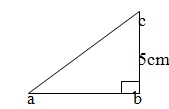
Q 6 - If ∆ ABC is an isosceles triangle with ∠ C = 90⁰ and AC = 5cm , Then AB =?
Answer : D
Explanation
Clearly BC =AC=5cm. AB2 = AC2+ BC2 =52 +52= 50 ⇒ AB = √50 = 5√2 cm.
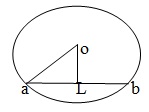
Q 7 - A chord of length 30cm is at a distance of 8cm from the center of a circle . The radius of the circle is
Answer : D
Explanation
Let O be the centre of the circle and AB be the chord. Draw OL ⊥ AB. Then AL= 1/2 AB = (1/2 *30)cm =15 cm and OL = 8cm. OA2 = OL2 +AL2= 82 + (15)2 = (64 + 225 ) =289 ⇒ OA = √289 = 17cm. ∴ Radius of the circle is 17 cm.
Q 8 - In the given figure ,ABCD is a cyclic quadrilateral in which AB || DC and ∠ BAD = 100⁰. Then , ∠ ABC=?
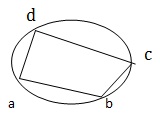
Answer : B
Explanation
AB DC and AD is the transversal. ∴ ∠ADC + ∠DAB=180⁰ ⇒ ADC =100⁰ =180⁰ ⇒ ADC=80⁰. Opposite angles of a cyclic quadrilateral are supplementary. ∴ ∠ADC +∠ABC = 180⁰ ⇒ 80⁰+ ∠ABC =180⁰ ⇒ ABC = 100⁰.
Q 9 - AB and CD are two parallel chords on the opposite sides of the center of the circle. If AB = 10cm , CD= 24cm and the radius of the circle is 13cm, the distance between the chords is
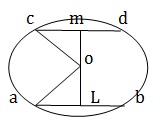
Answer : A
Explanation
From O draw OL⊥ AB and OM CD. Join OA and OC. AL = 1/2 AB = 5cm , OA = 13 cm. OL2 = OA2 - AL2 = (13) 2 - 52 = (169 - 25) = 144 ⇒ OL = √144 = 12 cm. Now ,CM =1/2 * CD =12 cm and OC =13cm. ∴ OM2 = OC2 - CM2 = (13) 2 - (12) 2 = (169 - 144) = 25 ⇒ OM =√ 25 = 5cm. ∴ ML = OM + OL = (5+12 ) cm =17cm.
Answer : C
Explanation
∠ADC +∠ EDC = 180⁰ ⇒ ∠ADC + 120⁰ = 180⁰ ⇒ ∠ADC= 60⁰ ∠ABC = ∠ADC = 60⁰ ( s in the same segment).